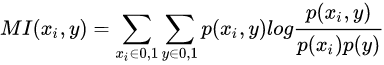pearson特征选择matlab,常用的特征选择方法之 Pearson 相关系数

众所周知，特征选择是机器学习活动至关重要的一步。最理想的情况下，我们把所有影响目标的独立因素给找出来，然后使用合适的量化手段，就能够得到完美描述目标问题的特征列表，用这些特征去建立合适容量的模型，这样的模型能够完美的匹配我们要解决的任务。

但是实际上这种想法太难实现了，我们往往只能从已有的数据出发，通过一些特征变换和组合得到一些原始特征，然后从这些原始特征中选出与目标相关的特征。

随着深度网络的崛起，越来越多的未经复杂变换的原始特征被加入到了深度网络中，大家期待有用的特征能够被自动的抽取和组合出来。但是这并不意味着特征工程就不需要了，推荐系统的大牛 Xavier 在技术博客《Rules of Machine Learning: Best Practices for ML Engineering》中提到很多关于特征工程的建议，非常值得一读，其中包含的思想就是特征是随着系统的优化进程而逐步添加的，并非一蹴而就，要始终保证特征的简单、直观、可复用、可监控和可靠性，这意味着我们需要时常对系统中存量特征做测试和筛选。

特征选择通常有过滤法(Filter)、打包法(Wrap)和嵌入法(Embed)，其中，后两者都是与模型相关的，需要具体问题具体对待，而过滤法是指对特征进行预处理，提前过滤掉一些对目标无益(即对模型无益)的特征，它只考虑任务目标，而与模型无关。

我打算把常用的特征选择方法都再回顾一遍，力争把每种方法都讲得通俗易懂。这篇文章先介绍 Pearson 相关系数。

Pearson 相关系数的定义

Pearson 相关系数是用来检测两个连续型变量之间线性相关的程度，取值范围为 $[-1,1]$，正值表示正相关，负值表示负相关，绝对值越大表示线性相关程度越高。在实际做特征工程时候，如果两个变量的相关系数取值为负，可以将特征变量取负号，使之与目标变量正相关，这样来保证所有特征与目标之间都是正相关。

两个变量之间的 Pearson 相关系数定义为两个变量之间的协方差和标准差的商：

上式定义了总体相关系数，常用希腊小写字母 $\rho$ 作为代表符号。估算样本的协方差和标准差，可得到样本 Pearson 相关系数，用英文小写字母 $r$ 表示：

记 $\boldsymbol{x}’=\boldsymbol{x}-\overline{x}$ 和 $\boldsymbol{y}’=\boldsymbol{y}-\overline{y}$ 表示对变量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 进行 $0$ 均值化，则实际上 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 的 Pearson 相关系数就是 $\boldsymbol{x}’$ 和 $\boldsymbol{y}’$ 的 cosine 相似度：$r_{\boldsymbol{x},\boldsymbol{y}}=\cos(\boldsymbol{x}’,\boldsymbol{y}’)=\frac{\boldsymbol{x}’\cdot\boldsymbol{y}’}{|\boldsymbol{x}’|\cdot|\boldsymbol{y}’|}$。

Pearson 相关系数的使用条件

使用 Pearson 相关系数之前需要检查数据是否满足前置条件：

两个变量间有线性关系；

变量是连续变量；

变量均符合正态分布，且二元分布也符合正态分布；

两变量独立；

两变量的方差不为 0；

这些条件在实际中很容易被忽略。

例如，在视频推荐中，我们可以将用户对视频的播放完成度作为目标变量，检测其他连续型特征与它的相关性，或者将这些连续型特征做特定的变换后，检测其与播放完成度的相关性。

但是播放完成度实际上不是正态分布的，如下图所示(实际上大多数日志统计特征，如用户播放视频数、视频播放完成度等，也都不服从正态分布)，因此实际上是不能使用 Pearson 相关系数的，这时候可以用 Spearman 或者 Kendall 相关系数来代替。

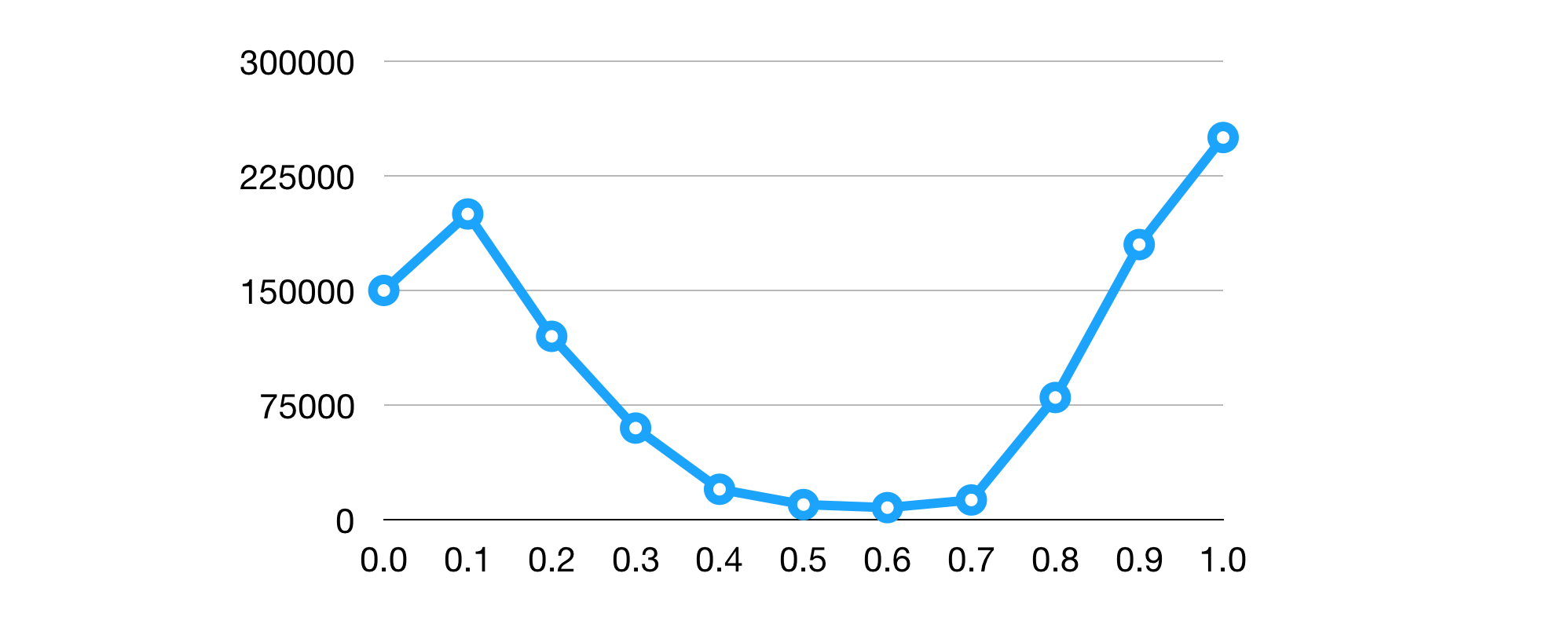
另外要注意的是，如果两个变量本身就是线性的关系，那么 Pearson 相关系数绝对值越大相关性越强，绝对值越小相关性越弱；但在当两个变量关系未知情况下，Pearson 相关系数的大小就没有什么指导意义了，它的绝对值大小并不能表征变量间的相关性强弱，这个时候最好能够画图出来看看作为辅助判断。我会在下面的例子里再详细的说明这一点。

举例说明

我们举个例子来看如何计算 Pearson 相关系数(这里仅仅演示计算过程，实际上数据的分布也不满足使用 Pearson 相关系数的条件)。

考虑视频推荐场景下，假设我们的目标 (之一) 是最大化视频的播放完成度 $y$，播放完成度的取值范围是 $[0,1]$，我们需要分析哪些因素跟 $y$ 相关，例如有一维特征是表示用户对视频的偏好度，记为 $x$，它的取值范围也是 $[0,1]$，我们把几条样本中 $x$ 和 $y$ 的取值计算出来，并画成散点图，如下所示：

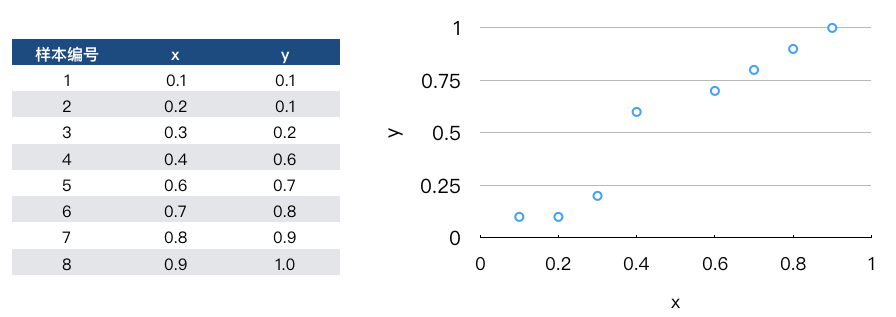
我们可以按照公式 (2) 来计算 $x$ 与 $y$ 的 Pearson 相关系数：

计算变量平均值：$\overline{x} = 0.5,\ \overline{y}=0.55$；

计算平移后的变量：$\boldsymbol{x}=[-0.4,-0.3,-0.2,-0.1,0.1,0.2,0.3,0.4]$，$\boldsymbol{y}=[-0.45,-0.45,-0.35,0.05,0.15,0.25,0.35,0.45]$；

计算公式 (2) 的结果：$r=\frac{0.73}{\sqrt{0.6}\cdot\sqrt{ 0.94}}=0.972$；

通过计算，我们发现，这个特征与目标变量之间的线性相关性非常高，这与我们看图得到的认知是一致的。因此我们可以把这一维特征作为有效特征加入。

但是，如果我们对这个例子稍加修改，将最后一个数据点 $(0.9,1.0)$ 改为 $(0.9,-1.0)$，如图 3 所示：

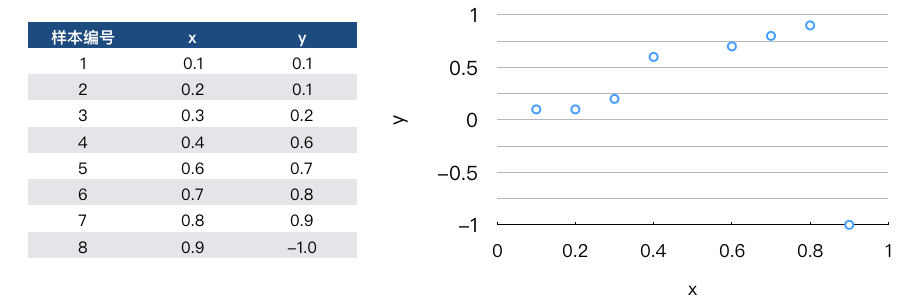
从我们的观察来看，最后一个数据点可能是噪声或者异常值，对我们判断两个变量的线性相关性应该不造成影响，但是实际上，我们再次计算一下这两个变量的 Pearson 相关系数，此时的值仅仅只有 $-0.0556$，可以说是几乎不线性相关了，这说明 Pearson 相关系数小并不代表线性相关性一定弱。在这种情况下，我们应该在数据清洗阶段把特征的异常值过滤或者平滑掉以后，再计算它与目标的相关系数。

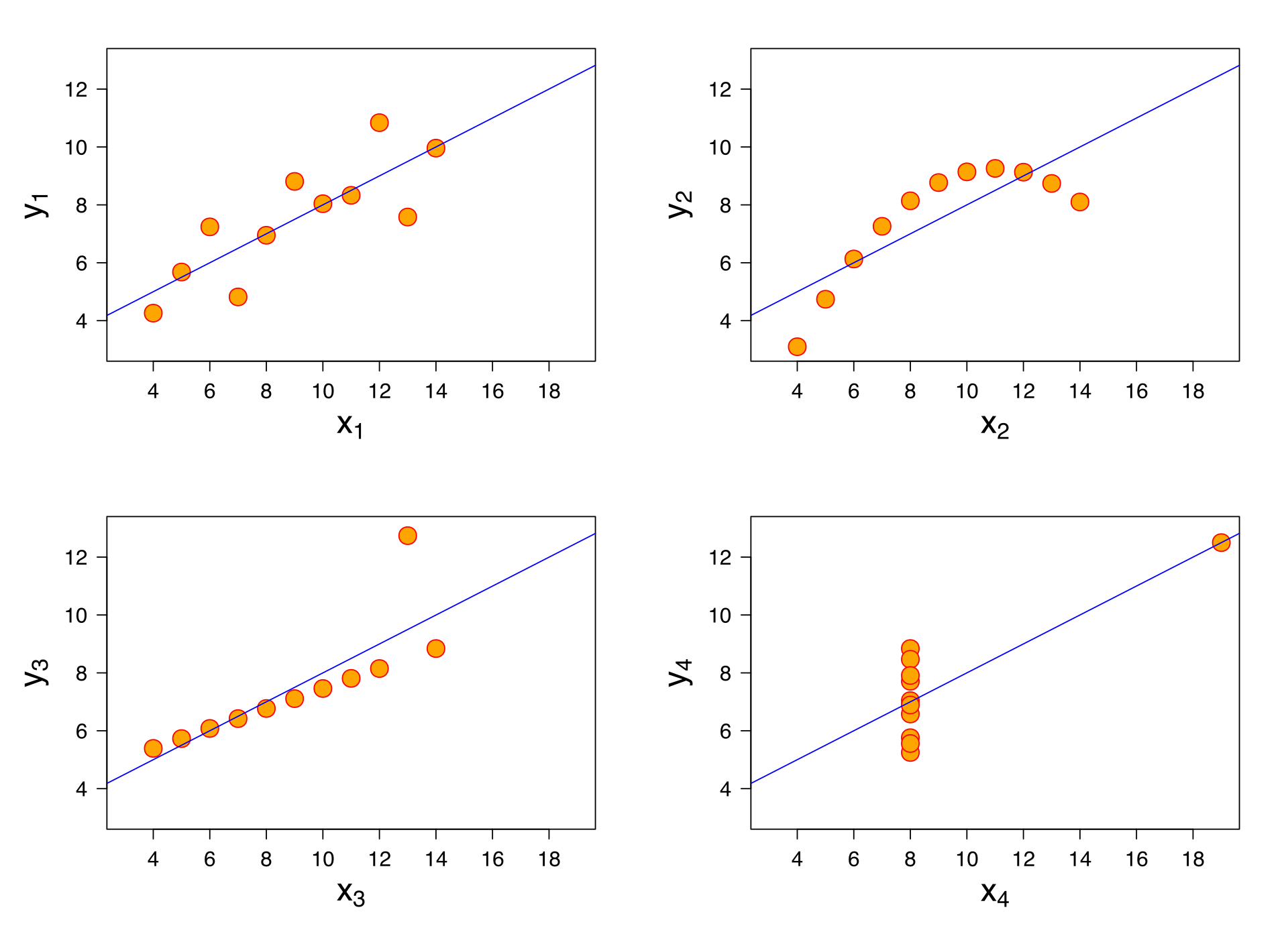
反过来，Pearson 相关系数大也并不代表线性相关性一定强。图 4 列举了几个 Pearson 相关系数均为 $0.816$ 的变量数据，其中有些变量间并非明显的线性相关，或者是明显的二次相关，只是 Pearson 相关系数恰好较大而已。