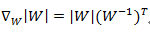【机器学习】独立成分分析(ICA)及Matlab实现

独立成分分析及Matlab实现

- 1.问题引入
- 2.ICA原理
- 3.ICA算法步骤
- 4.性质与优点
- 5.程序代码
- 6.程序分析
- 7.运行结果

1.问题引入

独立成分分析（ICA）最初由Aapo Hyvärinen等人于1980年代提出，其起源可以追溯到对神经科学和信号处理领域的研究需求。ICA的提出主要是为了解决混合信号中盲源分离、非高斯性信号处理和自适应性估计等问题，为实际应用提供了一种有效的信号处理方法。随着研究的深入和应用的广泛，ICA在语音信号处理、图像处理、金融数据分析、生物医学信号处理等领域都得到了广泛应用。

2.ICA原理

独立成分分析（ICA）是一种用于从混合信号中分离出原始独立成分信号的统计信号处理方法。ICA 假设混合信号是由若干个相互独立的信号源线性组合而成的，而目标是通过观测到的混合信号来估计原始的独立成分信号。

ICA 的基本原理是通过找到一组变换，将混合信号转换为一组相互独立的信号。这些变换通常通过最大化信号的非高斯性（非高斯性通常意味着信号是非均匀分布的，例如正态分布的信号是高斯分布的，而非高斯分布的信号则可能是非均匀分布的）来实现。这是因为混合信号中的独立成分信号通常具有更高的非高斯性，而混合信号中的噪声和干扰通常更加接近高斯分布。

ICA 在很多应用领域中都有广泛的应用，例如信号处理、图像处理、语音处理、生物医学信号处理等。它具有许多优点，例如能够从多个混合信号中分离出独立成分信号，不需要事先对信号进行统计性质假设，适用于非高斯信号和非线性混合模型，具有较强的数学理论基础等。然而，ICA 也有一些限制和假设，例如需要混合矩阵满足一定条件、对噪声和干扰敏感等。因此，在应用 ICA 时需要谨慎选择合适的方法和技术参数，以确保结果的可靠性。

3.ICA算法步骤

数据准备：收集混合信号数据，将混合信号构成数据矩阵 X，其中每一行表示一个混合信号，每一列表示在不同时间或空间上的观测。
数据预处理：对数据进行预处理，例如去均值化（使数据的均值为零）和归一化（使数据的方差为一）等。
确定独立成分个数：根据实际应用场景和需求，确定独立成分的个数。
选择ICA算法：选择合适的ICA算法进行独立成分分析，常用的算法包括最大似然估计（MLE）、最大峰度（Maximizing Kurtosis）、信息最大化（Maximizing Mutual Information）等。
应用ICA算法：使用选定的ICA算法对数据进行处理，通过寻找一组变换矩阵或滤波器，将混合信号转换为一组相互独立的信号。
估计混合矩阵：在某些情况下，需要估计混合矩阵 A，它是将原始独立成分信号线性组合成混合信号的矩阵。
信号恢复：通过乘上逆混合矩阵 A^{-1}，将得到的独立成分信号重新映射到原始信号空间中，从而得到估计的原始独立成分信号。
结果分析：对ICA分解的结果进行分析和解释，包括信号的幅度、相位、频率等特性，可以通过可视化、统计分析等方法进行结果验证和评估。
可选的后处理：根据具体应用的需要，可以进行额外的后处理步骤，例如信号的滤波、降噪、特征提取等。
结果解释：根据实际应用需求和领域知识，对ICA分解得到的独立成分信号进行解释和解读，从而得到有意义的结论和应用结果。

4.性质与优点

分离能力：ICA能够从混合信号中分离出独立的成分信号，即通过ICA可以将混合信号还原为原始的独立成分信号，从而实现信号的分离和解混。
非高斯性假设：ICA不依赖于信号的高斯性假设，而是利用信号的统计独立性来进行分析和处理。这使得ICA在处理非高斯性信号，如峰值信号、脉冲信号等方面具有优势。
适用性广泛：ICA在许多领域中都有应用，包括信号处理、图像处理、语音处理、生物医学信号处理、金融数据分析等，具有广泛的适用性。
数据无损处理：ICA不会丢失原始信号的信息，因为它通过线性组合和逆变换来恢复原始信号，从而实现了数据的无损处理。
自适应性：ICA不需要先验知识或训练样本，而是通过自适应地估计混合矩阵和独立成分信号，因此对于未知的信号和混合情况也能进行有效处理。
可解释性：ICA分解得到的独立成分信号在某些情况下具有直观的解释性，可以用于解读和理解数据中的特征、结构和模式。
可扩展性：ICA可以与其他信号处理方法和机器学习方法相结合，形成更加强大的数据处理和分析工具，例如ICA与支持向量机（SVM）、神经网络、小波变换等方法的结合。
实时性：ICA可以在实时或在线处理中应用，适用于需要实时信号分析和处理的应用场景。
鲁棒性：ICA对于一些常见的干扰和噪声具有一定的鲁棒性，能够在一定程度上抵抗干扰和噪声的影响。
可并行性：ICA算法中的一些计算步骤可以并行处理，从而可以在多核处理器或并行计算环境中进行高效计算，加快处理速度。

5.程序代码

% 导入 FastICA 工具箱
addpath('fastica');% 生成合成信号
Fs = 1000;          % 采样频率
t = 0:1/Fs:5;       % 时间范围
f1 = 10;            % 信号1的频率
f2 = 50;            % 信号2的频率
A = [1, 0.5; 0.5, 2]; % 混合矩阵
s1 = sin(2*pi*f1*t); % 信号1
s2 = sawtooth(2*pi*f2*t); % 信号2
S = [s1; s2];       % 信号矩阵
X = A * S;          % 混合信号% 添加高斯噪声
rng(123);           % 设定随机数种子以保证结果的可重复性
mu = [0, 0];        % 噪声均值
sigma = [0.1, 0.1]; % 噪声标准差
n = mvnrnd(mu, sigma, length(t)); % 生成高斯噪声
X = X + n';         % 添加噪声到混合信号% 进行 ICA 分解
[icasig, A, W] = fastica(X, 'lastEig', 2);% 显示原始信号和ICA分解结果
figure;
subplot(3, 1, 1);
plot(t, S(1, :));
title('原始信号1');
subplot(3, 1, 2);
plot(t, S(2, :));
title('原始信号2');
subplot(3, 1, 3);
plot(t, icasig(1, :), 'r', 'LineWidth', 1.5);
hold on;
plot(t, icasig(2, :), 'b', 'LineWidth', 1.5);
title('ICA分解结果');
legend('ICA分解结果1', 'ICA分解结果2');

6.程序分析

首先，程序生成了两个合成信号，分别是一个频率为 10 Hz 的正弦信号和一个频率为 50 Hz 的锯齿波信号，并将它们存储在一个矩阵 S 中。然后，通过一个混合矩阵 A 将这两个信号线性混合生成混合信号 X，其中混合矩阵 A 是一个 2x2 的矩阵，控制了混合信号中每个信号的权重。
接下来，程序为混合信号 X 添加了高斯噪声，使用 mvnrnd 函数生成了一个具有指定均值和标准差的多元高斯分布的噪声，并将噪声添加到混合信号 X 中。
然后，程序调用了 FastICA 工具箱的 fastica 函数，对混合信号 X 进行 ICA 分解。fastica 函数返回了独立成分信号 icasig、混合矩阵 A 和分离矩阵 W。独立成分信号 icasig 是通过 ICA 分解得到的估计的源信号，混合矩阵 A 是用于生成混合信号 X 的混合过程的逆过程，分离矩阵 W 是通过 ICA 分解得到的逆变换矩阵。
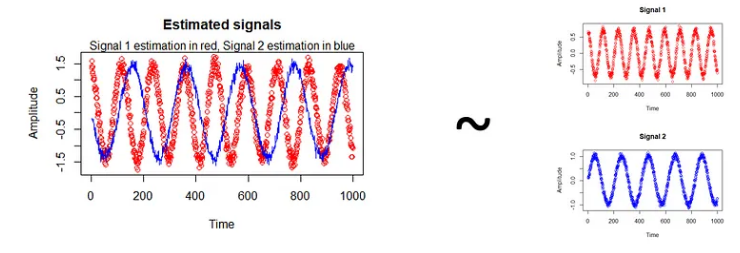
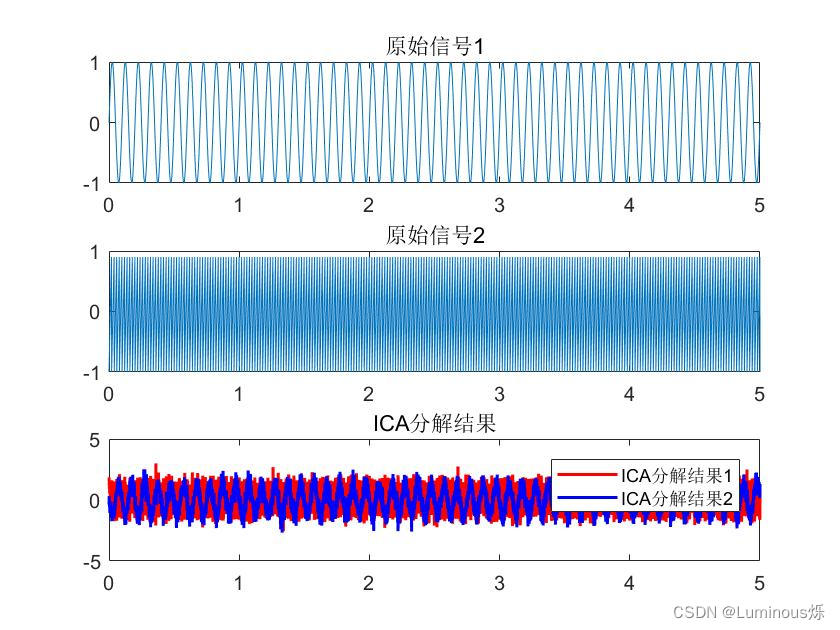
最后，程序使用 subplot 和 plot 函数将原始信号和ICA分解结果进行可视化展示，其中第一个子图展示了原始信号1，第二个子图展示了原始信号2，第三个子图展示了ICA分解得到的独立成分信号1和信号2，分别用红色和蓝色表示，并使用 legend 函数添加了图例。

这段 MATLAB 程序演示了如何使用 FastICA 工具箱进行独立成分分析（ICA）。