MNE-Python | 使用 ICLabel 模型进行 ICA 并自动修复样本

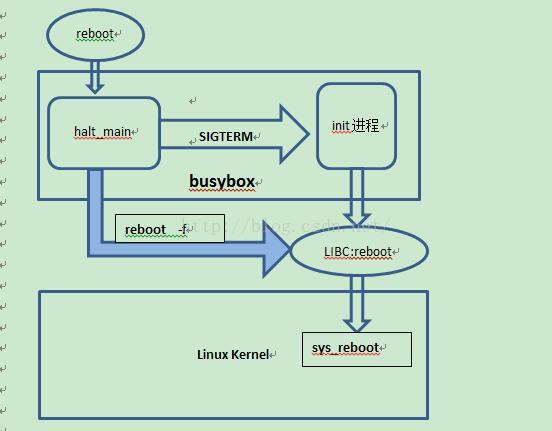
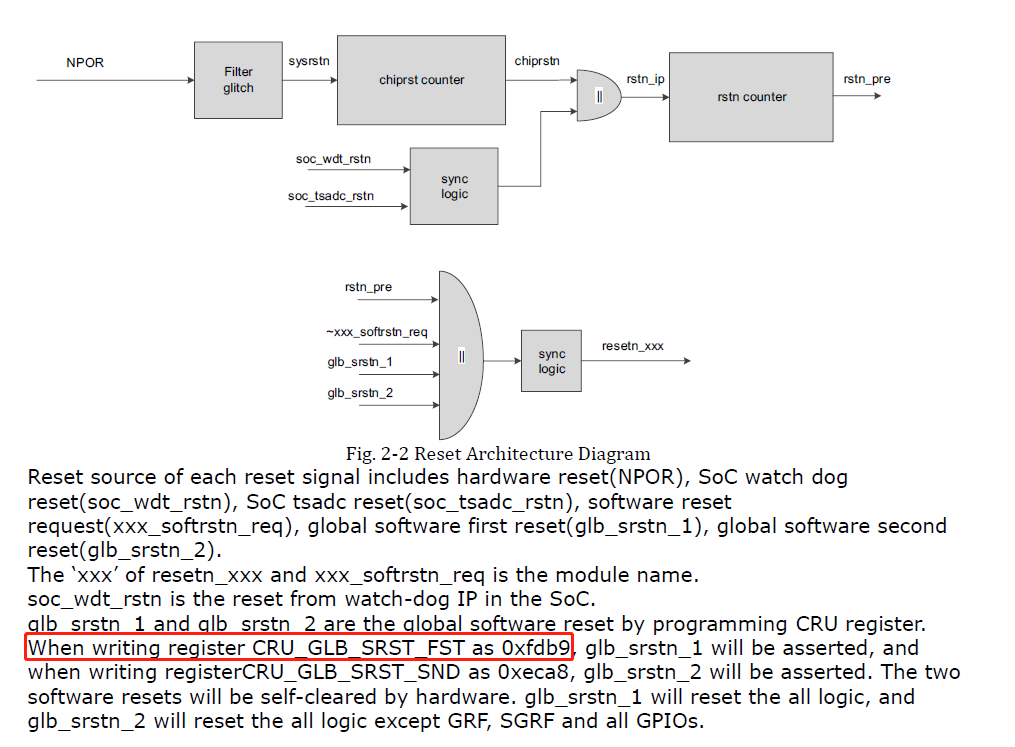
本文涵盖了使用 ICA 和 ICLabel 模型 1 自动修复信号，该模型源自 EEGLab。有关 ICA 的概念背景，请参阅此 scikit-learn 教程。有关如何使用 ICA 删除工件的基本了解，请参阅 MNE-Python 中的教程。

ICLabel 旨在对配备最大信号 ICA 分解算法的独立成分（IC）进行分类，该算法需要 EEG 数据集采用平均值作为重参考并在 [1，100] Hz 之间进行滤波处理。也可以在不符合这些规范的数据集上运行 ICLabel，但分类性能可能会受到负面影响。此外，ICLabel 论文没有研究这些预处理步骤的影响。

同样的我们需要导入必要的 Python 模块并加载一些示例数据。因为 ICA 的计算量很大，可以将数据裁剪为 60 秒；为了避免重复预处理（mne.preprocessing），我们将直接从该子模块导入一些函数和类。

import mne
from mne.preprocessing import ICAfrom mne_icalabel import label_componentssample_data_folder = mne.datasets.sample.data_path() / "MEG" / "sample"
sample_data_raw_file = sample_data_folder / "sample_audvis_raw.fif"
raw = mne.io.read_raw_fif(sample_data_raw_file)# 我们裁剪 60 秒的信号段，并删除 MEG 通道
raw.crop(tmax=60.0).pick_types(eeg=True, stim=True, eog=True)
raw.load_data()

输出为：

Opening raw data file C:\Users\Mathieu\mne_data\MNE-sample-data\MEG\sample\sample_audvis_raw.fif...Read a total of 3 projection items:PCA-v1 (1 x 102)  idlePCA-v2 (1 x 102)  idlePCA-v3 (1 x 102)  idleRange : 25800 ... 192599 =     42.956 ...   320.670 secs
Ready.
Removing projector <Projection | PCA-v1, active : False, n_channels : 102>
Removing projector <Projection | PCA-v2, active : False, n_channels : 102>
Removing projector <Projection | PCA-v3, active : False, n_channels : 102>
Reading 0 ... 36037  =      0.000 ...    60.000 secs...

Measurement date	December 03, 2002 19:01:10 GMT
Experimenter	MEG
Participant	Unknown
Digitized points	146 points
Good channels	9 Stimulus, 59 EEG, 1 EOG
Bad channels	None
EOG channels	EOG 061
ECG channels	Not available
Sampling frequency	600.61 Hz
Highpass	0.10 Hz
Lowpass	172.18 Hz
Filenames	sample_audvis_raw.fif
Duration	00:01:00 (HH:MM:SS)

滤波去除缓慢低频漂移

在运行 ICA 之前，一个重要的步骤是对数据的低频漂移进行过滤，低频漂移会对 ICA 拟合的质量产生负面影响。缓慢漂移的问题在于它们降低了假定为独立来源相互之间的独立性（例如，在缓慢向上漂移期间，神经、心跳、眨眼和其他肌电信号都会呈现出更高的值），使得算法更难找到准确的解。所以建议使用截止频率为 1 Hz 的高通滤波器。但是，由于滤波是线性操作，从滤波后的信号中找到的 ICA 解可以应用于未滤波的信号，参考以下文献：

Irene Winkler, Stefan Debener, Klaus-Robert Müller, and Michael Tangermann. On the influence of high-pass filtering on ICA-based artifact reduction in EEG-ERP. In Proceedings of EMBC-2015, 4101–4105. Milan, 2015. IEEE. doi:10.1109/EMBC.2015.7319296.

因此我们将保留未滤波的原始对象的副本，以便我们可以将 ICA 的解作用与原始数据。

filt_raw = raw.copy().filter(l_freq=1.0, h_freq=100.0)

输出为：

Filtering raw data in 1 contiguous segment
Setting up band-pass filter from 1 - 1e+02 HzFIR filter parameters
---------------------
Designing a one-pass, zero-phase, non-causal bandpass filter:
- Windowed time-domain design (firwin) method
- Hamming window with 0.0194 passband ripple and 53 dB stopband attenuation
- Lower passband edge: 1.00
- Lower transition bandwidth: 1.00 Hz (-6 dB cutoff frequency: 0.50 Hz)
- Upper passband edge: 100.00 Hz
- Upper transition bandwidth: 25.00 Hz (-6 dB cutoff frequency: 112.50 Hz)
- Filter length: 1983 samples (3.302 sec)[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done   1 out of   1 | elapsed:    0.0s remaining:    0.0s
[Parallel(n_jobs=1)]: Done   2 out of   2 | elapsed:    0.0s remaining:    0.0s
[Parallel(n_jobs=1)]: Done   3 out of   3 | elapsed:    0.0s remaining:    0.0s
[Parallel(n_jobs=1)]: Done   4 out of   4 | elapsed:    0.0s remaining:    0.0s
[Parallel(n_jobs=1)]: Done  59 out of  59 | elapsed:    0.0s finished

拟合并绘制ICA解

现在即可准备开始建立并拟合ICA。通过观察原始数据可以知道 EOG 和 ECG 的伪影影响很强，所以我们预计这些伪影将在 ICA 之前发生的 PCA 分解的前几个维度中被捕获。因此可能不需要大量的成分来区分数据（尽管有时需要更多的成分来获得更准确的解）。首先可以做尝试，我们将使用n_components=15 运行 ICA（仅使用前 15 个 PCA 成分来计算 ICA 分解）——考虑到我们的数据有 59 个良好的 EEG 通道，成分数量相对较小，但其优势在于它可以快速运行，我们将能够轻松判断它是否有效（因为我们已经知道 EOG / ECG 伪影应该是什么样子）。

ICA 拟合具有不确定性（例如，提取出的成分可能会在不同的计算中出现符号翻转，或者可能并不总是以相同的顺序返回），因此我们还将指定一个随机种子，以便每次本教程都获得相同的结果由我们的网络服务器构建。

在拟合 ICA 之前，我们将应用一个共同的平均重参考，以符合 ICLabel 的要求。

filt_raw = filt_raw.set_eeg_reference("average")

输出为：

EEG channel type selected for re-referencing
Applying average reference.
Applying a custom ('EEG',) reference.

我们将使用 “extended infomax” 方法来拟合 ICA，以符合 ICLabel 要求。 ICLabel 未与其他 ICA 分解算法进行测试，但其性能和准确性不应受算法影响。

ica = ICA(n_components=15,max_iter="auto",method="infomax",random_state=97,fit_params=dict(extended=True),
)
ica.fit(filt_raw)
ica

输出为

Fitting ICA to data using 59 channels (please be patient, this may take a while)
Selecting by number: 15 components
Computing Extended Infomax ICA
Fitting ICA took 3.3s.

Method	infomax
Fit	500 iterations on raw data (36038 samples)
ICA components	15
Explained variance	91.0 %
Available PCA components	59
Channel types	eeg
ICA components marked for exclusion	—

我们可以传递给 fit函数方法的一些可选参数包括 decim（在计算 IC 时仅使用每第 N 个样本，可提升快速性）和reject（拒绝每种通道类型提供最大可接受幅值范围的区间）。

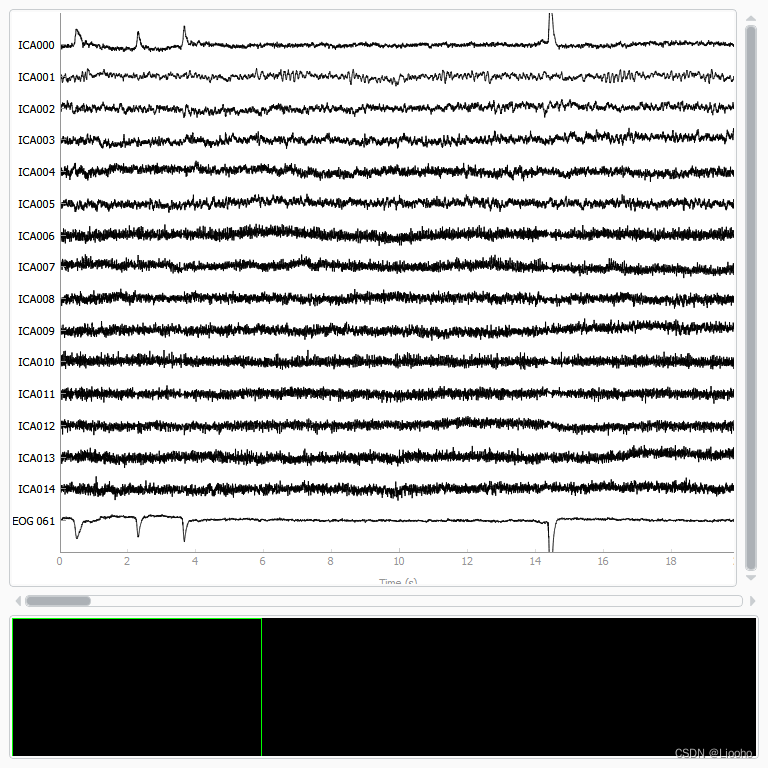
现在我们可以查看 IC 以查看它们捕获的内容。 plot_sources 将显示 IC 的时间序列。请注意，在我们对 plot_sources 的调用中，我们可以使用原始的、未过滤的 Raw 对象：

raw.load_data()
ica.plot_sources(raw, show_scrollbars=False, show=True)

输出为：

Creating RawArray with float64 data, n_channels=16, n_times=36038Range : 25800 ... 61837 =     42.956 ...   102.956 secs
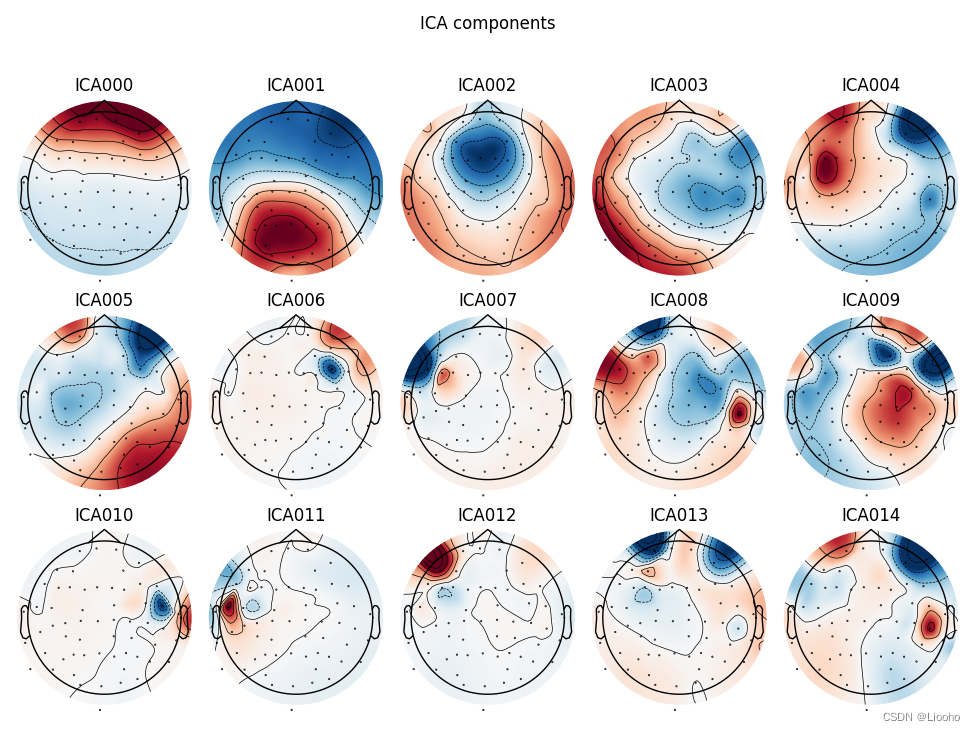
Ready.

我们可以很清楚地看到第一个成分 (ICA000) 捕获了 EOG 信号。我们可以用plot_components 可视化每个组件的头皮场分布。这些是基于 ICA 混合矩阵中的值进行插值的：

ica.plot_components()# blinks
ica.plot_overlay(raw, exclude=[0], picks="eeg")

输出为：

Applying ICA to Raw instanceTransforming to ICA space (15 components)Zeroing out 1 ICA componentProjecting back using 59 PCA components

我们还可以使用 plot_properties 单独绘制 IC 图：

ica.plot_properties(raw, picks=[0])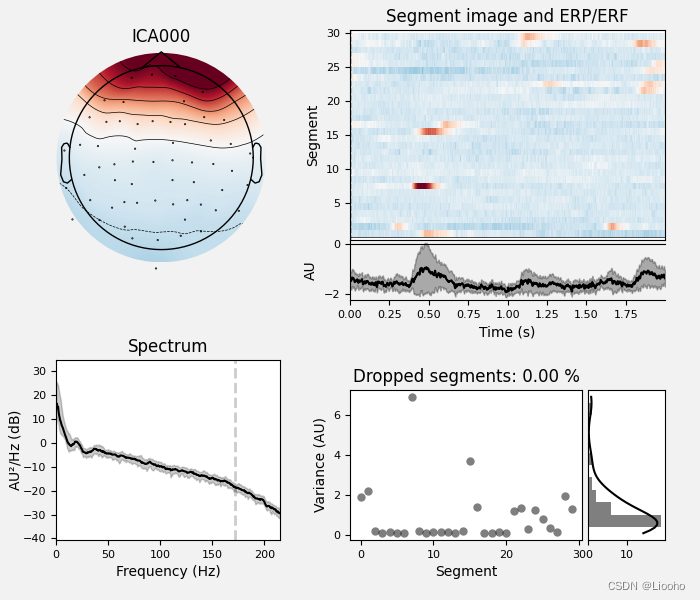

输出为：

    Using multitaper spectrum estimation with 7 DPSS windows
Not setting metadata
30 matching events found
No baseline correction applied
0 projection items activated

自动选择 ICA 成分

我们可以应用自动 ICA 标记算法，该算法将输出以下七个成分的概率值：

brain
muscle artifact
eye blink
heart beat
line noise
channel noise
other

ICLabel label_components 函数的输出按顺序为这些类中的每一个生成预测概率值。详见文献：

Luca Pion-Tonachini, Ken Kreutz-Delgado, and Scott Makeig. Iclabel: an automated electroencephalographic independent component classifier, dataset, and website. NeuroImage, 198:181–197, 2019. URL: https://www.sciencedirect.com/science/article/pii/S1053811919304185, doi:https://doi.org/10.1016/j.neuroimage.2019.05.026.

ic_labels = label_components(filt_raw, ica, method="iclabel")# 例如：ICA0 可以准确地识别为眨眼，ICA12 被归为肌肉伪影。
print(ic_labels["labels"])
ica.plot_properties(raw, picks=[0, 12], verbose=False)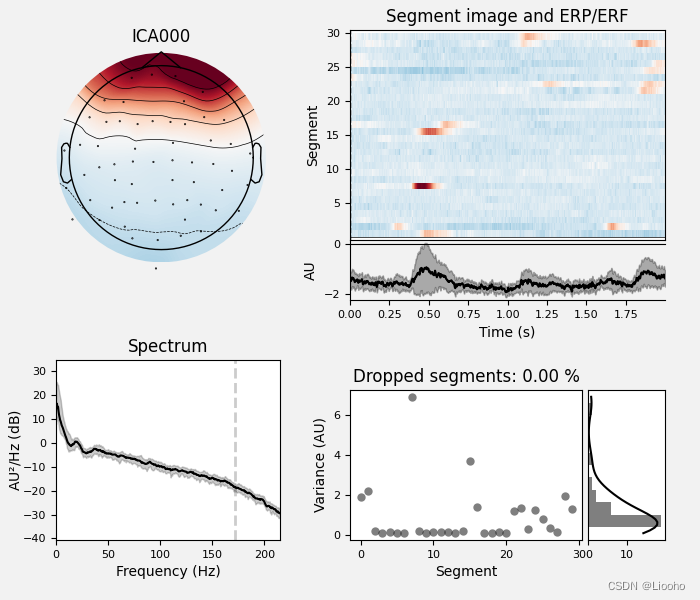

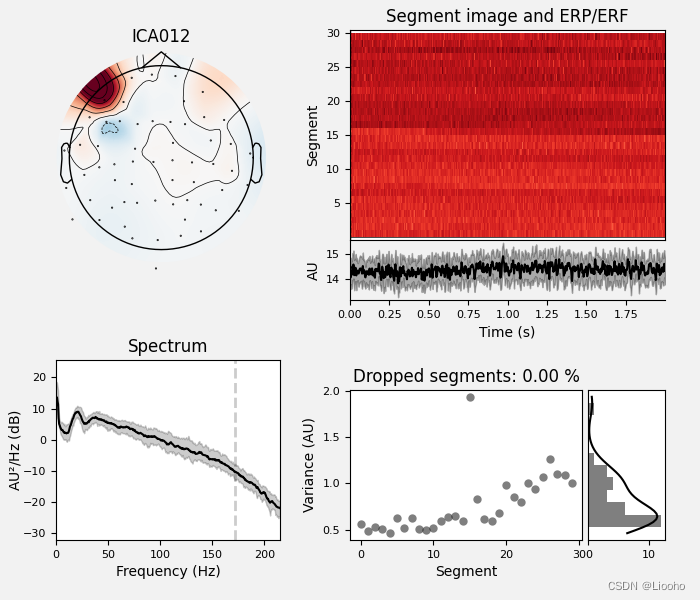
print输出结果：

['eye blink', 'brain', 'brain', 'brain', 'brain', 'brain', 'muscle artifact', 'muscle artifact', 'other', 'brain', 'muscle artifact', 'muscle artifact', 'muscle artifact', 'muscle artifact', 'eye blink']

提取标签并重构原始数据

我们可以提取出所有不属于大脑的成分，保留“大脑”和“其他”。 “其他”是不可分类的成分。保险起见，并假设我们不能盲目地删除这些成分。

labels = ic_labels["labels"]
exclude_idx = [idx for idx, label in enumerate(labels) if label not in ["brain", "other"]]
print(f"Excluding these ICA components: {exclude_idx}")

输出为：

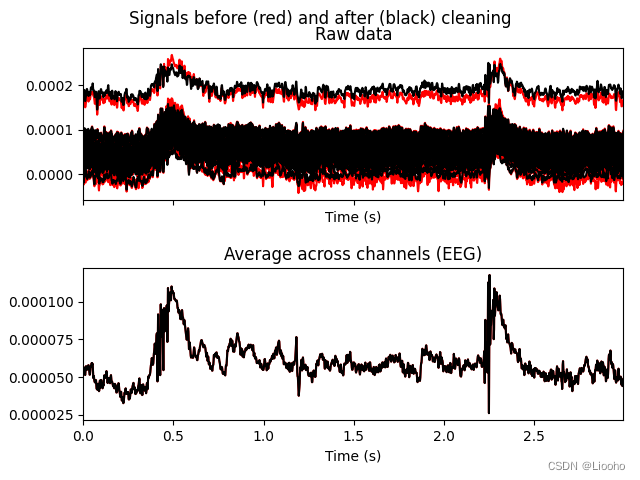
Excluding these ICA components: [0, 6, 7, 10, 11, 12, 13, 14]

现在我们有了需要被剔除的成分，可以用 mne.apply 去除每个通道上信号的伪影，需要注意的是，我们要将对于过滤后的数据得到的 ICA 解决方案作用于原始未滤波的信号。将原始的数据与重构后的数据一同绘制，心跳和眨眼的伪影已得到修复。

# ica.apply() changes the Raw object in-place, so let's make a copy first:
reconst_raw = raw.copy()
ica.apply(reconst_raw, exclude=exclude_idx)raw.plot(order=artifact_picks, n_channels=len(artifact_picks), show_scrollbars=False)
reconst_raw.plot(order=artifact_picks, n_channels=len(artifact_picks), show_scrollbars=False)
del reconst_raw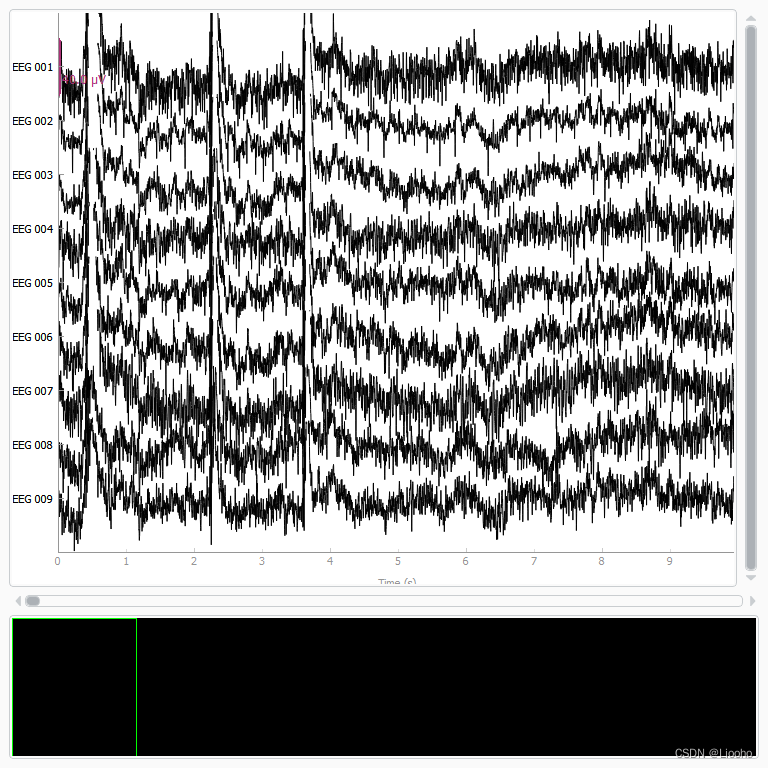

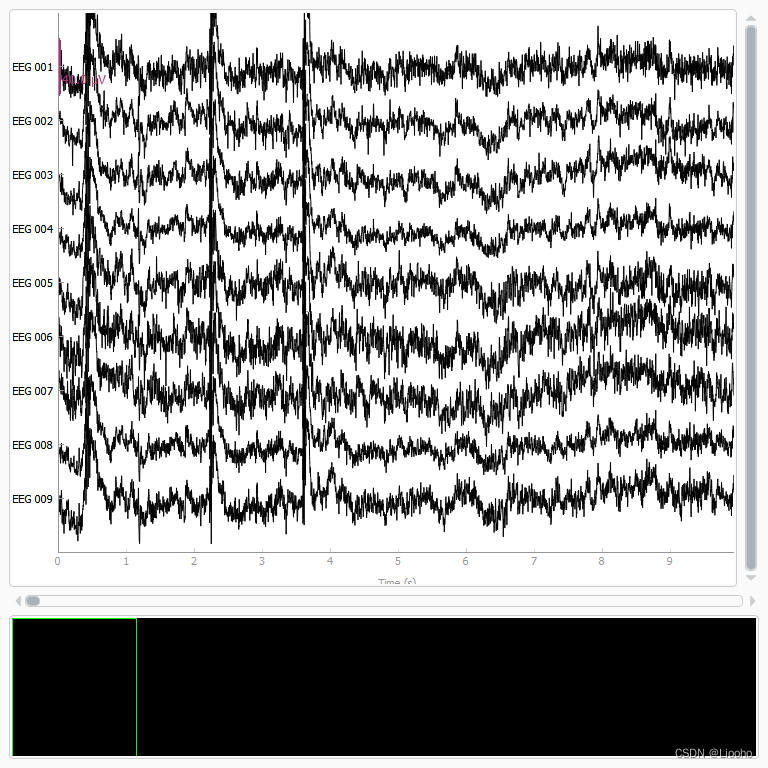
输出为：

Applying ICA to Raw instanceTransforming to ICA space (15 components)Zeroing out 8 ICA componentsProjecting back using 59 PCA components