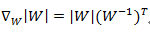Background
做一个数据分析业务之前,往往需要对反映事物的多个特征变量进行大量的观测,收集大量数据以便进行分析寻找规律。多个特征变量确实会提供丰富的信息,但是很多情况下变量之间可能会存在相关性,如果用全部特征变量去拟合模型,可能在训练集的效果上会表现的很好,但是在测试集的效果上可能很差。这就存在模型(过度自信)的问题。因此需要找到一种合理的方法,在减少需要分析的特征变量同时,尽量减少特征变量包含信息的损失,以达到对所收集数据进行全面分析的目的。
数据降维
降维字面意思就是降低维度,简单解释就是将重复的特征变量(重复值这两个变量之间关系紧密)删去多余,也就是要建立更少的新特征变量,使得这些新的特征变量互不相关,并且这些新变量还能够保持反映业务问题的主要信息。
降维主要优点:
- 去除噪声
- 降低计算复杂度
- 使得数据集更易使用
- 使得结果更易理解
降维常见方法: - 主成分分析(PCA)
- 奇异值分解(SVD)
- 线性判决分析(LDA)
- 独立成分分析(ICA)
- 因子分析(FA)
- t-分布领域嵌入算法(T-SNE)
- Others I don’t know
PCA与ICA
PCA:主成分分析是一种常用的降维算法,可通过线性组合的方法将多个特征综合为少数特征,且综合后的特征相互独立,有可以表示原始特征的大部分信息。
PCA理解:某数据含有1000样本,其中每组数据有100个特征变量,现在想把特征变量变为10个,即可通过主成分分析将shape为(1000,100)的数据变成shape为(1000,10)的数据。

这里原数据的100个特征变量变成后面的10个新变量,而这10个新变量又分别是由这100个旧变量组成。详细解释如下图:

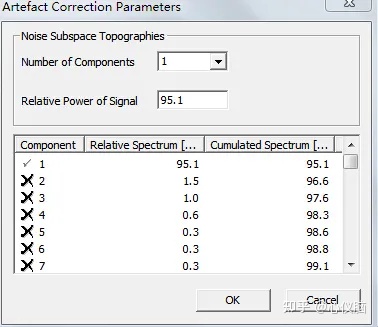
注意:由主成分分析得到的新的10个变量,也就是得到新模型a1b1+a2b2+…a10b10后,可将特征值b1~b10按照从大到小排列,并作贡献度分析,求出进一步的对问题占主要帮助的特征,一般选取贡献度为85%-95%的特征做进一步的主成分。
举例说明:比如筛选后b1,b2,b3的累计贡献率超过85%,则最终将a1,a2,a3作为该样本的主成分,从而实现降维。
PCA求解步骤:
- 求数据协方差矩阵(为了判断两个数据的特征关系)
- 计算协方差矩阵的特征值和特征变量
- 特征值从大到小排序做贡献度分析
- 选出最终主成分,并将数据转换到有新的特征向量构建的新数据空间中
主成分的真正意义: - 新的变量由旧的变量组成但不一定以旧的变量来描述新的变量
- 降维一般是为了更好地回归或者分类,所以PCA只是一个过程结果,用来辅助构建模型
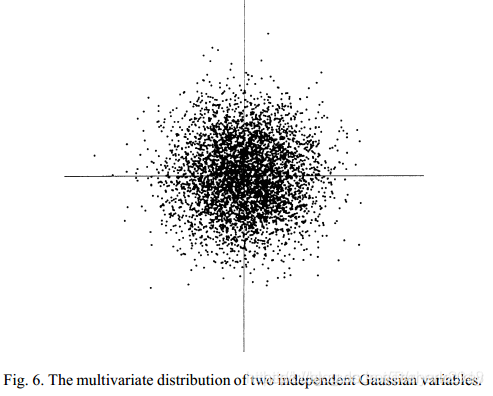
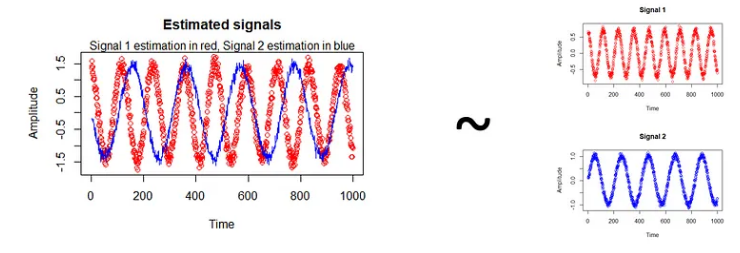
ICA:独立成分分析最早应用于盲源信号分离。起源于“鸡尾酒会问题”,描述如下:在嘈杂的鸡尾酒会上,许多人在同时交谈,可能还有背景音乐,但人耳却能准确而清晰的听到对方的话语。这种可以从混合声音中选择自己感兴趣的声音而忽略其他声音的现象称为“鸡尾酒会效应”。对于盲源分离问题,ICA是指在只知道混合信号,而不知道源信号、噪声以及混合机制的情况下,分离或近似的分离出源信号的一种分析过程。ICA是一种用来从多变量(多维)统计数据里找到隐含的因素或成分的方法,被认为是PCA和FA的一种扩展。
ICA模型:

ICA理论的目标是在只有观察数据的情况下,求得一个分离矩阵W(又称解混矩阵),随后利用分离矩阵W来分离观察数据X,使得获得成分Y是独立源成分S的最优逼近。
常用ICA算法:
- Informax ICA
- Extend ICA
- Fast ICA
其中,FastICA是对搜索算法的改进!改进之处在于:改善了传统梯度的收敛速度。
ICA与PCA主要区别:
- PCA是将数据降维并提取出不相关的属性,而ICA是将数据降维并提取出相互独立的属性(不相关就是两者没有线性关系,但是不排除其他关系的存在,独立就是互不相关没有关联)
- ICA认为观测信号是若干个统计独立的成分的线性组合,ICA要做的是一个解混过程来找到这些独立源成分。而PCA是一个信息提取过程,将原数据降维,现已成为ICA将数据标准化的预处理步骤。
python解析
- 借助sklearn模块里面的PCA模块实现

数据结果:


- 不借助工具包sklearn实现
主要步骤:- 原始数据组成N*M维度矩阵
- 将原始数据每一行进行零均值化
- 求出原始数据的协方差矩阵
- 求出协方差矩阵对应的特征值以及对应的特征向量
- 特征向量按对应特征值大小从上到下按行列排成矩阵,根据实际业务场景,取贡献度操作一定范围的前N行构成矩阵W
- Y=WX就是降到N维后的目标矩阵数据(X为原始数据)


最后说明:在实际使用PCA的过程中,正确估计用于描述数据的成分的数量是非常重要的环节,可以将累积方差贡献率看做关于成分数量的函数,从而确定所需要的成分的数量,上图结果曲线量化了前N个成分中包含了多少总的64维度的方差,可以看到30维度可以保持97的方差。