机器学习的起点——线性回归

一、线性回归的地位

首先，线性回归中最基础的概念是一元线性回归模型。
在回归模型中，线性回归模型是最简单的。其具备两个优势：第一是线性回归模型适合于大数据。训练时消耗的计算资源较少。第二是模型本身具备很好的可解释性。属于“白盒模型”。

二、线性回归的定义

线性回归主要是包括“线性”和“回归”两部分。线性是指其具有线性的决策边界，其中在二维空间里，其决策边界就是一条直线。回归表明其具有预测功能。
二维数据可视化，观察其线性性。高维数据可以先用PCA降维再可视化观察其线性性
这里的任务就成了，如何使用一条线对这些散点进行拟合。我们应该用什么样的标准来评判，那条线是拟合这些散点最好的线呢？

通过直觉我们感觉，蓝色线是拟合程度最好的一条线。那么这个“直觉”从哪里来？我们应当如何整理和表达这个直觉？这个直觉有数学依据吗？

以上三个问题。我们一一来解答：

第一，这个直觉从哪里来？答案是来自于我们脑子里现有的经验模型，换句话说是一种感觉。

第二，这个直觉怎么表达？答案是，这个直觉我们可以依托于一个误差函数来表达。我们采用的目标函数是测量真实值和预测值之间的差异。我们使用平方误差函数。

第三，这个直觉有数学依据吗？答案是有的，极大似然估计就是其数学依据，注意这个问题跟第二个问题是有区别的。

三、一元线性回归的代码实现（手写和使用sklearn两种方式）

# 创建数据集，把数据写入到numpy数组
import numpy as np  # 引用numpy库，主要用来做科学计算
import matplotlib.pyplot as plt   # 引用matplotlib库，主要用来画图
data = np.array([[152,51],[156,53],[160,54],[164,55],[168,57],[172,60],[176,62],[180,65],[184,69],[188,72]])# 打印大小
x, y = data[:,0], data[:,1]
print (x.shape, y.shape)# 1. 手动实现一个线性回归算法
# TODO: 实现w和b参数， 这里w是斜率， b是偏移量
x_mean = np.mean(x) 
y_mean = np.mean(y)
xy_mean = np.mean(x.dot(y))
x_2_mean = np.mean(x.dot(x))
w =((xy_mean)-(x_mean*y_mean))/(x_2_mean)-x_mean*x_mean
b = y_mean-w*x_mean print ("通过手动实现的线性回归模型参数: %.5f %.5f"%(w,b))# 2. 使用sklearn来实现线性回归模型, 可以用来比较一下跟手动实现的结果
from sklearn.linear_model import LinearRegression
model = LinearRegression().fit(x.reshape(-1,1),y)
print ("基于sklearn的线性回归模型参数：%.5f %.5f"%(model.coef_, model.intercept_))

四、多元线性回归

1、模型介绍

（1）模型结构

多元线性回归模型通常用来描述变量y和x之间的随机线性关系：
在这里插入图片描述
当你获得诸多样本点之后，分别代入上式，可以得到一个方程组。这一方程组用矩阵表示如下：

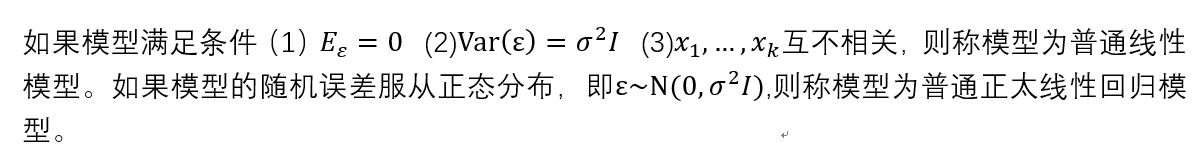
在这里插入图片描述

（2）模型参数的确定（最小二乘估计）

在高斯假定（上面的几个条件）下，如果X是列满秩的，则我们定义的“损失函数最小化”其实就是最小二乘法的过程。则参数的最小二乘估计为：
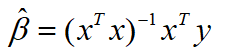
在这里插入图片描述

这一最小二乘估计的过程，其实就包含了使得损失函数（损失值与真实值之差的平方和）最小的优化过程。经过这一过程，我们才得到这个参数估计结果。而在这个优化过程中，我们在求解最优解析解的过程中，使用了梯度下降法(Gradient Descent)，它是一个循环迭代式的算法。另外，在线性回归中，它不受特征之间线性相关的影响。

（3）参数的显著性检验

这里涉及到拟合优度检验、怀特检验等等诸多能够衡量估计出来的参数的优劣的检验方法。属于计量经济学和序列分析相关的内容，这部分检验的过程具体与本文无关。暂不表。

（4）多元线性回归的代码实现

import numpy as np
from sklearn.linear_model import LinearRegression# 生成样本数据， 特征维度为2
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
# y = 1 * x_0 + 2 * x_1 + 3
y = np.dot(X, np.array([1, 2])) + 3# 先使用sklearn自带的库来解决
model = LinearRegression().fit(X, y)# 打印参数以及偏移量（bias）
print ("基于sklearn的线性回归模型参数为 coef: ", model.coef_, " intercept: %.5f" %model.intercept_)# 手动实现参数的求解。先把偏移量加到X里
a = np.ones(X.shape[0]).reshape(-1,1)
X = np.concatenate((a, X), axis=1)# 通过矩阵、向量乘法来求解参数， res已经包含了偏移量
res = np.matmul(np.linalg.inv(np.matmul(X.T, X)),  np.matmul(X.T, y))# 打印参数以偏移量（bias）
print ("通过手动实现的线性回归模型参数为 coef: ", res[1:], " intercept: %.5f"%res[0])

2、数学原理分析

通过上一节中的三个问题我们知道，这种“最小二乘法”拟合的操作有依据吗？答案是有的，极大似然估计就是其数学依据。下面我们从数学角度介绍为什么采用真实值和预测值之差的平方和在数学上是最优的。

因为：

线性回归的最小二乘法是基于误差为高斯分布这一假设得来的

首先在我们做回归分析的过程中，必然会出现大量的误差，这对每一个样本点都是可能的。

我们把误差看作是随机变量，在模型确定的条件下，每一个样本都对应一个误差值。那么问题就是：如果把所有的误差搜集起来，他们会有什么特点呢？

根据大数定理，一旦样本个数越来越多，这些误差会慢慢服从正态分布。

这就是最小二乘法最核心的假设。基于此我们可以得出以下关于条件概率的结论：
在这里插入图片描述
这样我们对每一个样本的条件概率就建立了起来。接下来我们只需要基于样本之间的独立性，针对所有样本构造最大似然概率。进而求参数。
我将构建过程手写如下：

最后总结，我们从数学的角度可以清楚地看到如下的结论：
在这里插入图片描述