学习笔记,仅供参考,有错必纠
文章目录
- 时间序列
- 误差修正模型
- F检验
- 似然比(LR)检验
- W检验
- LM乘数检验
- LR, W和LM检验
- 自相关的LM检验
时间序列
误差修正模型
在用“一般到特殊”方法建立模型时的,首先应对初始模型(即对回归参数不加任何约束的动态分布滞后模型)的随机误差项进行异方差和自相关检验。对模型的其他检验都应建立在随机误差项是一个白噪声序列的基础之上。在检验约束条件是否成立的过程中逐步剔除不显著变量,化简模型,同时还要保持模型随机误差项的非自相关性和同方差性不被破坏。在这个过程中要用到许多统计量.
F检验
把样本数据取对数后建立回归模型,随机误差项一般不会存在异方差。对于随机误差项的一阶自相关检验可用DW统计量完成。对于ADL(1,1)模型,约束条件 α 1 = 0 , β 1 = 0 , β 0 = 0 \alpha_1 = 0, \beta_1 = 0, \beta_0 = 0 α1=0,β1=0,β0=0和 α 1 + β 0 + β 1 − 1 = 0 \alpha_1 + \beta_0 + \beta_1 - 1 = 0 α1+β0+β1−1=0是否成立可用t检验完成。如果t统计量的绝对值大于临界值,则相应约束条件不成立,相应解释变量不能轻易地从模型中剔除掉。否则接受相应约束条件,从模型中剔除相应解释变量。
对于联合线性约束条件可用F检验完成。假定模型误差项服从正态分布,共有m个线性约束条件,则所用统计量是 :
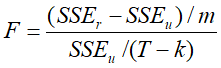
在零假设“约束条件真实”条件下, F ∼ F ( m , T − k ) F \sim F(m, T-k) F∼F(m,T−k).
因为两个模型都是用OLS法估计的,所以可把被解释变量的总平方和(SST)分解为回归平方和 (SSR) 与误差平方和(SSE)两部分。
对于不加约束的模型有:
SST = SSRu + SSEu .
对于施加约束条件的模型有:
SST = SSRr + SSEr .
如果约束条件成立,那么在施加约束条件下求到的SSEr 不会比不加约束条件的SSEu大很多,用样本计算的F值不会很大。
若F值小于临界值,则约束条件是可接受的(真实的)。否则应该拒绝零假设。
注意,F检验的零假设是m个约束条件同时为零,备择假设是m个约束条件不同时为零。所以拒绝零假设并不排除有部分约束条件为零。应利用t检验进一步对每一个参数进行显著性判别。
比如对ADL(1,1)模型,检验联合约束条件 α 1 = β 1 = 0 \alpha_1 = \beta_1 = 0 α1=β1=0,则:

似然比(LR)检验
以上介绍的t检验和F检验只适用于对线性约束条件的检验。对于非线性约束条件, α 1 β 0 + β 1 = 0 \alpha_1 \beta_0 + \beta_1 = 0 α1β0+β1=0,则无法用t或F检验完成。下面介绍三种常用的检验方法,即:
似然比(LR)检验;
沃尔德(W)检验;
拉格朗日(lagrange)乘数(LM)检验。
这三种检验所用统计量都是利用极大似然估计法计算的。LR检验由内曼—皮尔逊(Neyman-Pearson 1928)提出,只适用于对线性约束的检验。W检验和LM检验既适用于对线性约束条件的检验,也适用于对非线性约束条件的检验。
LR检验的基本思路是如果约束条件成立则相应约束模型与非约束模型的极大似然函数值应该是近似相等的。
下式表示非约束模型的极大似然函数:
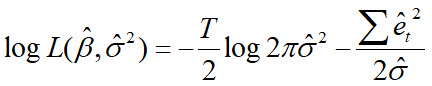
其中 β ^ \hat{\beta} β^和 σ ^ 2 \hat{\sigma}^2 σ^2分别是对 β \beta β(参数集合), σ 2 \sigma^2 σ2的极大似然估计。
下式表示约束模型的极大似然函数:
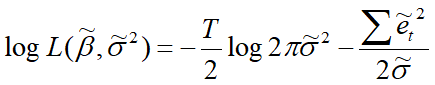
其中 β ~ \tilde{\beta} β~和 σ ~ 2 \tilde{\sigma}^2 σ~2分别是对 β \beta β(参数集合), σ 2 \sigma^2 σ2的极大似然估计。
定义似然比(LR)统计量为:
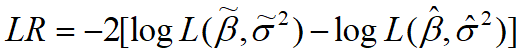
中括号内是两个似然函数之比(似然比检验由此而得名)。在零假设约束条件成立条件下:
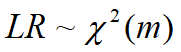
其中m表示约束条件个数。用样本计算LR统计量。判别规则是:
若 L R < χ α 2 ( m ) LR < \chi^2_{\alpha}(m) LR<χα2(m) , 则接受零假设,约束条件成立。
若 L R > χ α 2 ( m ) LR > \chi^2_{\alpha}(m) LR>χα2(m) , 则拒绝零假设,约束条件不成立。
ADL(1,1)模型,检验联合约束条件 α 1 = β 1 = 0 \alpha_1 = \beta_1 = 0 α1=β1=0,则:

LR统计量只适用于对线性约束条件的检验。对非线性约束条件应该采用如下两种检验方法。
W检验
W检验的优点是只需估计无约束模型。当约束模型的估计很困难时,此方法尤其适用。W检验由沃尔德(Wald 1943)提出,适用于线性与非线性约束条件的检验。
W检验的原理是测量无约束估计量与约束估计量之间的距离。先举一个简单例子。比如对模型:
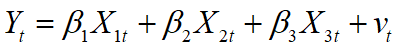
检验线性约束条件 β 2 = β 3 \beta_2 = \beta_3 β2=β3是否成立。W检验只需对无约束模型进行估计,因为对约束估计量 β ~ 2 \tilde{\beta}_2 β~2和 β ~ 3 \tilde{\beta}_3 β~3来说,必然有 β ~ 2 − β ~ 3 = 0 \tilde{\beta}_2 - \tilde{\beta}_3 = 0 β~2−β~3=0。如果约束条件成立,则无约束估计量 β ^ 2 − β ^ 3 \hat{\beta}_2 - \hat{\beta}_3 β^2−β^3应该近似为零。如果约束条件不成立,则无约束估计量应该显著地不为零。关键是要找到一个准则,从而判断什么是显著地不为零。

其中:
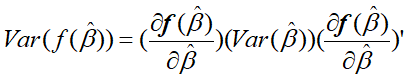
∂ f ( β ^ ) ∂ β ^ \frac{\partial f(\hat{\beta})}{\partial \hat{\beta}} ∂β^∂f(β^)表示用无约束估计量 代替后的偏导数矩阵,其中第i行第j列位置上的元素表示第i个约束条对第 j个无约束估计量的偏导数值. V a r ( β ^ ) Var(\hat{\beta}) Var(β^)是 β ^ ) \hat{\beta}) β^)的估计的方差协方差矩阵.
在约束条件成立条件下:

W统计量的具体表达式为:

在零假设 β 1 β 2 = β 3 \beta_1 \beta_2 = \beta_3 β1β2=β3成立条件下,W统计量近似服从 χ 2 ( 1 ) \chi^2(1) χ2(1)分布.
LM乘数检验
与W检验不同的是拉格朗日(Lagrange)乘数(LM)检验只需估计约束模型。所以当施加约束条件后模型形式变得简单时,更适用于这种检验。LM检验是由艾奇逊—西尔维(Aitchison-Silvey 1960)提出的。LM检验另一种表达式是由拉奥(Rao 1948)提出的,称为得分检验。
首先给出非约束模型的对数似然函数:
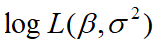
对于非约束极大似然估计量 β j ^ \hat{\beta_j} βj^必然有:
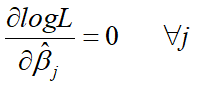

假定有两个约束条件f1(b)=0和f2(b)=0。为求这两个约束条件下的对数似然函数的极大似然估计量,应按拉格朗日乘数法则建立如下函数:


对于线性回归模型,通常是通过一个辅助回归式计算LM统计量的值。LM统计量与辅助回归式的可决系数 R 2 R^2 R2有直接联系,而辅助回归式的形式直接与被检验的约束条件有关。
LM检验的实际步骤如下:


- 例子
下面介绍用LM辅助回归方法检验约束条件 β 2 + β 3 = 1 \beta_2 + \beta_3 = 1 β2+β3=1:

LM检验的实际步骤:

- 实例(湾湾制造业生产函数)

(1)用OLS法估计约束模型,计算残差序列 u t ^ \hat{u_t} ut^:

(2)确定LM辅助回归式的解释变量。
(3)建立LM辅助回归式如下:
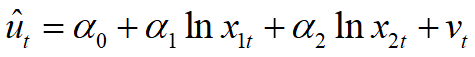
(4)用OLS法估计上式并计算可决系数 R 2 R^2 R2:
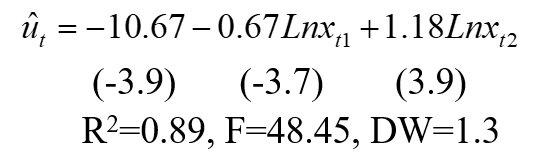
(5)用第四步得到的 R 2 R^2 R2计算LM统计量的值:
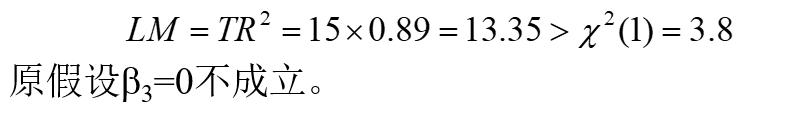
LR, W和LM检验
对LR,W和LM检验方法的选择应以做实际计算时的难易程度而定。一般来说W和LM检验应优于LR检验,因为W和LM检验只需要估计一个模型即可,而LR检验需估计约束与非约束两个模型。对W 和LM检验方法的选择应以约束模型与非约束模型哪个更容易估计而定。应该注意,即使三种检验方法都可使用,它们的计算结果通常也是不相同的。因为三个统计量只是渐近相同,对于线性回归模型,在小样本条件下有如下关系成立。:
L M ≤ L R ≤ W LM \le LR \le W LM≤LR≤W
上式说明只有当 LM检验的结果为拒绝零假设(约束条件不成立)或者W检验的结果为接受零假设(约束条件成立)时,三种检验的结论才是一致的。
实际中,三种检验方法有可能得出相互不一致的结论。另外只有当用参数的样本估计值计算的约束条件完全成立时,即把参数估计值代入约束条件能准确成立时,式中的三个统计量才有完全相等的关系。
当对数似然函数中只含有一个参数 β \beta β时,LM, LR 和W三种检验的关系可用图表示:

自相关的LM检验
DW统计量只适用于一阶自相关检验,而对于高阶自相关检验并不适用。利用LM统计量可建立一个适用性更强的自相关检验方法,既可检验一阶自相关,也可检验高阶自相关。
考虑两种误差过程的模型: