文章目录

反卷积的作用
卷积中padding的几个概念
- No Padding
- Half(Same) Padding
- Full Padding
反卷积
- 反卷积中的Padding参数
- 反卷积的stride参数
- 反卷积的output_padding参数
反卷积总结
参考资料

反卷积的作用

传统的卷积通常是将大图片卷积成一张小图片，而反卷积就是反过来，将一张小图片变成大图片。

但这有什么用呢？其实有用，例如，在生成网络(GAN)中，我们是给网络一个向量，然后生成一张图片

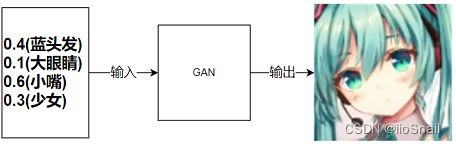
在这里插入图片描述

所以我们需要想办法把这个向量一直扩，最终扩到图片的的大小。

卷积中padding的几个概念

在了解反卷积前，先来学习传统卷积的几个padding概念，因为后面反卷积也有相同的概念

No Padding

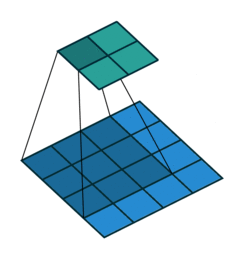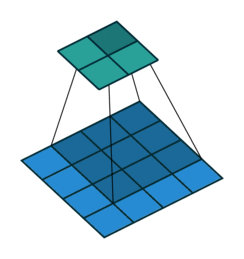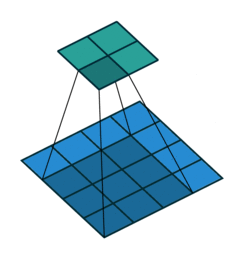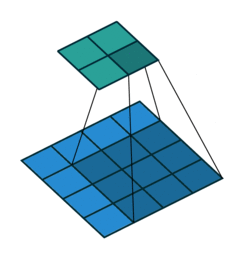
No Padding就是padding为0，这样卷积之后图片尺寸就会缩小，这个大家应该都知道

下面的图片都是蓝色为输入图片，绿色为输出图片。

Half(Same) Padding

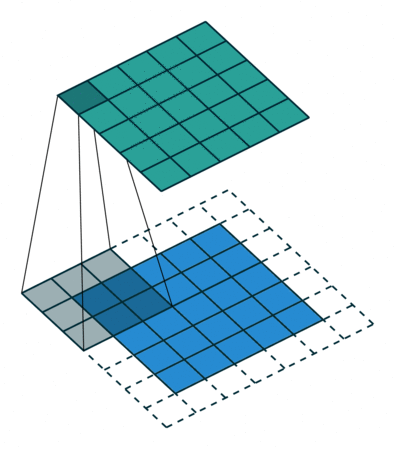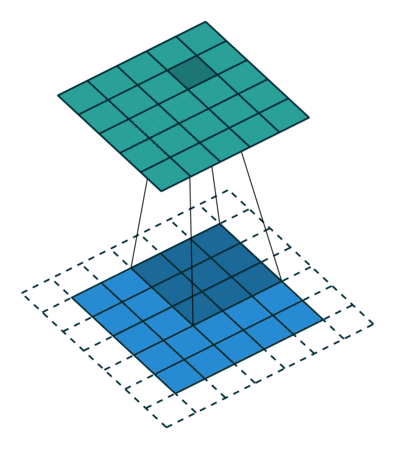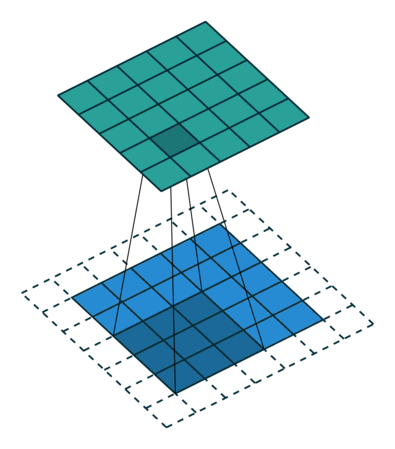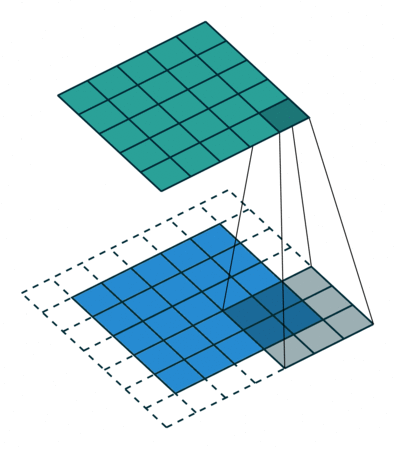
在这里插入图片描述
Half Padding也称为Same Padding，先说Same，Same指的就是输出的图片和输入图片的大小一致，而在stride为1的情况下，若想让输入输出尺寸一致，需要指定 $p=\lfloor k/2 \rfloor$ ，这就是 Half 的由来，即padding数为kerner_size的一半。

在 pytorch 中支持same padding，例如：

inputs = torch.rand(1, 3, 32, 32)
outputs = nn.Conv2d(in_channels=3, out_channels=3, kernel_size=5, padding='same')(inputs)
outputs.size()

torch.Size([1, 3, 32, 32])

Full Padding

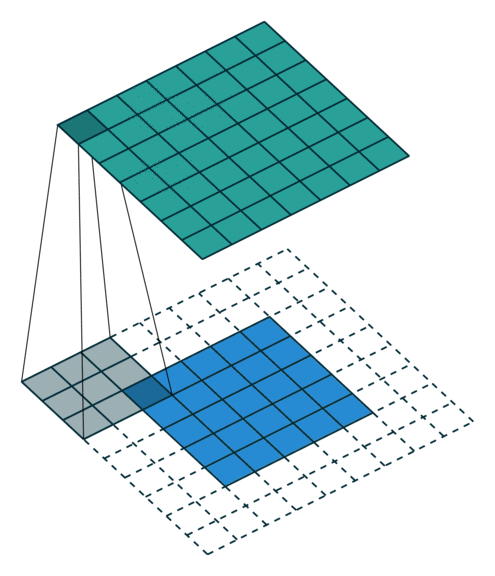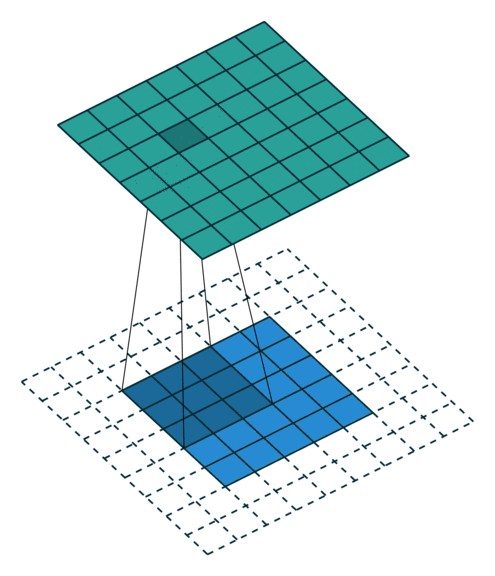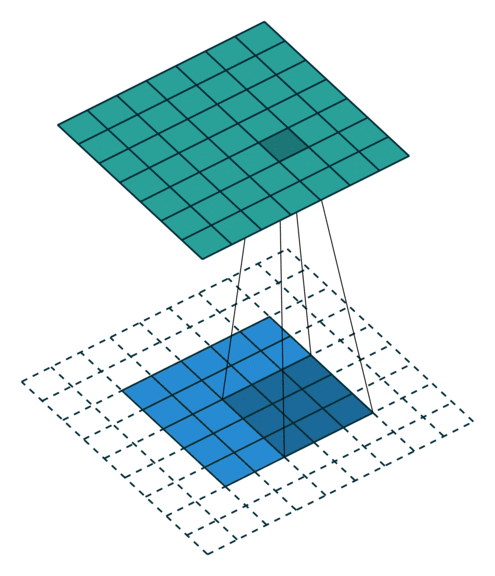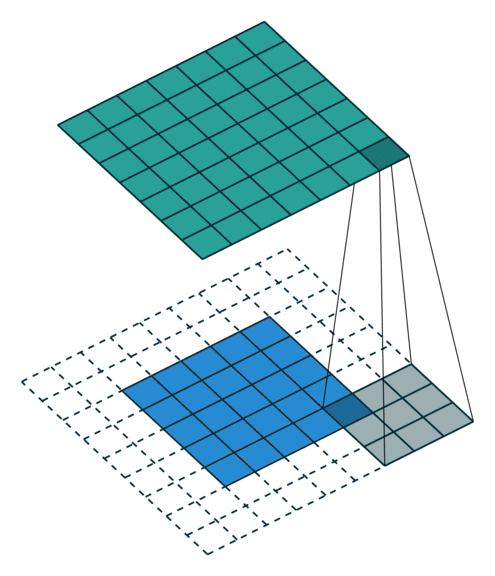
在这里插入图片描述

当 $p = k - 1$ 时就达到了 Full Padding。为什么这么说呢？可以观察上图， $k = 3$ ， $p = 2$ ，此时在第一格卷积的时候，只有一个输入单位参与了卷积。假设 $p = 3$ 了，那么就会存在一些卷积操作根本没有输入单位参与，最终导致值为0，那跟没做一个样。

我们可以用pytorch做个验证，首先我们来一个Full Padding：

inputs = torch.rand(1, 1, 2, 2)
outputs = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=2, bias=False)(inputs)
outputs

tensor([[[[-0.0302, -0.0356, -0.0145, -0.0203],[-0.0515, -0.2749, -0.0265, -0.1281],[ 0.0076, -0.1857, -0.1314, -0.0838],[ 0.0187,  0.2207,  0.1328, -0.2150]]]],grad_fn=<SlowConv2DBackward0>)

可以看到此时的输出都是正常的，我们将padding再增大，变为3：

inputs = torch.rand(1, 1, 2, 2)
outputs = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=3, bias=False)(inputs)
outputs

tensor([[[[ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000],[ 0.0000,  0.1262,  0.2506,  0.1761,  0.3091,  0.0000],[ 0.0000,  0.3192,  0.6019,  0.5570,  0.3143,  0.0000],[ 0.0000,  0.1465,  0.0853, -0.1829, -0.1264,  0.0000],[ 0.0000, -0.0703, -0.2774, -0.3261, -0.1201,  0.0000],[ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000]]]],grad_fn=<SlowConv2DBackward0>)

可以看到最终输出图像周围多了一圈 0，这就是部分卷积没有输入图片参与，导致无效了计算。

反卷积

反卷积其实和卷积是一样的，只不是参数对应关系有点变化。例如：

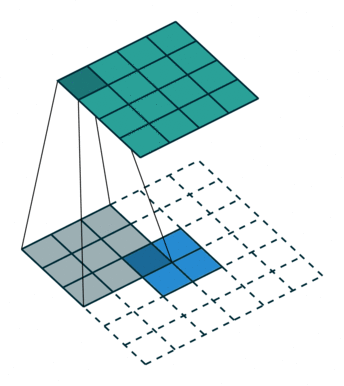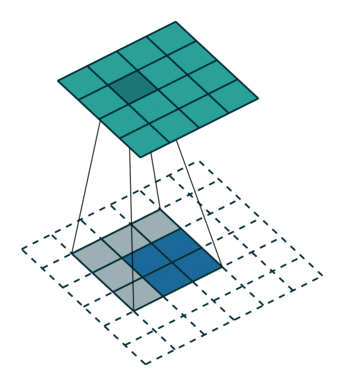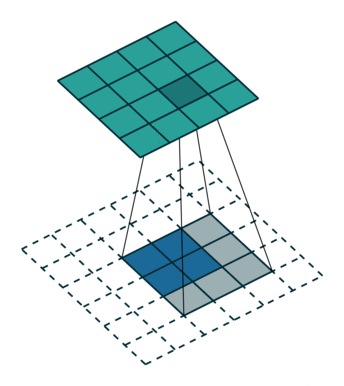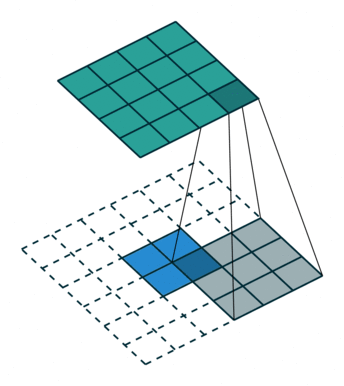
在这里插入图片描述
这是一个padding=0的反卷积，这时候你肯定要问了，这padding分明是2嘛，你怎么说是0呢？请看下面

反卷积中的Padding参数

在传统卷积中，我们的 padding 范围为 $[0, k - 1]$ ， $p = 0$ 被称为 No padding， $p = k - 1$ 被称为 Full Padding。

而在反卷积中的 $p^{'}$ 刚好相反，也就是 $p^{'} = k - 1 - p$ 。也就是当我们传 $p^{'} = 0$ 时，相当于在传统卷积中传了 $p = k - 1$ ，而传 $p^{'} = k - 1$ 时，相当于在传统卷积中传了 $p = 0$ 。

我们可以用如下实验进行验证：

inputs = torch.rand(1, 1, 32, 32)
# 定义反卷积，这里 p'=2, 为反卷积中的Full Padding
transposed_conv = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=3, padding=2, bias=False)
# 定义卷积，这里p=0，为卷积中的No Padding
conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=0, bias=False)
# 让反卷积与卷积kernel参数保持一致，这里其实是将卷积核参数的转置赋给了反卷积
transposed_conv.load_state_dict(OrderedDict([('weight', torch.Tensor(np.array(conv.state_dict().get('weight'))[:, :, ::-1, ::-1].copy()))]))
# 进行前向传递
transposed_conv_outputs = transposed_conv(inputs)
conv_outputs = conv(inputs)# 打印卷积输出和反卷积输出的size
print("transposed_conv_outputs.size", transposed_conv_outputs.size())
print("conv_outputs.size", conv_outputs.size())# 查看它们输出的值是否一致。
#（因为上面将参数转为numpy，又转了回来，所以其实卷积和反卷积的参数是有误差的，
# 所以不能直接使用==，采用了这种方式，其实等价于==）
(transposed_conv_outputs - conv_outputs) < 0.01

transposed_conv_outputs.size:  torch.Size([1, 1, 30, 30])
conv_outputs.size:  torch.Size([1, 1, 30, 30])tensor([[[[True, True, True, True, True, True, True, True, True, True, True,.... //略

从上面例子可以看出来，反卷积和卷积其实是一样的，区别就几点：

反卷积进行卷积时，使用的参数是kernel的转置，但这项其实我们不需要关心
反卷积的padding参数 $p^{'}$ 和传统卷积的参数 $p$ 的对应关系为 $p^{'} = k - 1 - p$ 。换句话说，卷积中的no padding对应反卷积的full padding；卷积中的full padding对应反卷积中的no padding。
从2中还可以看到一个事情，在反卷积中 $p^{'}$ 不能无限大，最大值为 $k - 1 - p$ 。（其实也不是哦）

题外话，不感兴趣去可以跳过，在上面第三点我们说了 $p^{'}$ 的最大值为 $k - 1 - p$ ，但实际你用pytorch实验会发现， $p^{'}$ 是可以大于这个值的。而这背后，相当于是对原始图像做了裁剪。

在pytorch的nn.Conv2d中，padding是不能为负数的，会报错，但有时可能你需要让padding为负数（应该没这种需求吧），此时就可以用反卷积来实现，例如：

inputs = torch.ones(1, 1, 3, 3)
transposed_conv = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=1, padding=1, bias=False)
print(transposed_conv.state_dict())
outputs = transposed_conv(inputs)
print(outputs)

OrderedDict([('weight', tensor([[[[0.7700]]]]))])
tensor([[[[0.7700]]]], grad_fn=<SlowConvTranspose2DBackward0>)

上述例子中，我们传给网络的是图片：

$\begin{bmatrix} 1 & 1 &1 \\ 1 & 1 &1 \\ 1 & 1 &1 \end{bmatrix}$

但是我们传的 $p^{'} = 1, k = 1$ ，这样在传统卷积中相当于 $p = k - 1 - p^{'} = - 1$ ，相当于 Conv2d(padding=-1)，这样在做卷积时，其实是对图片 $[1]$ 在做卷积（因为把周围裁掉了一圈），所以最后输出的尺寸为 $(1, 1, 1, 1)$

这个题外话好像没啥实际用途，就当是更加理解反卷积中的padding参数吧。

反卷积的stride参数

反卷积的stride这个名字有些歧义，感觉起的不怎么好，具体什么意思可以看下图：

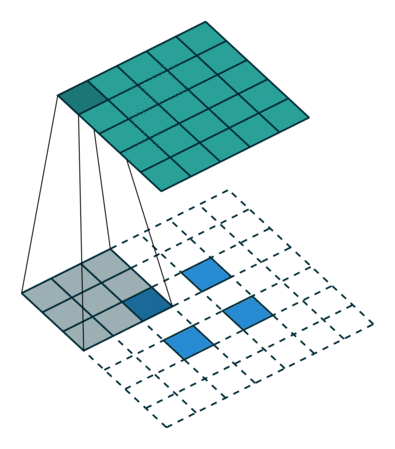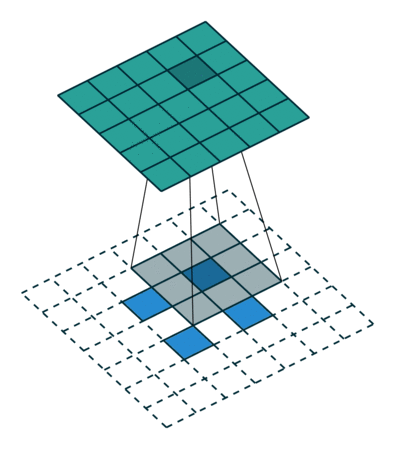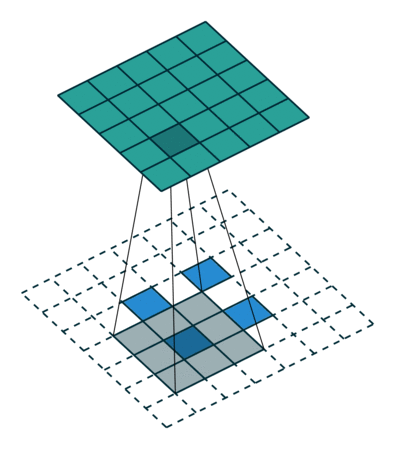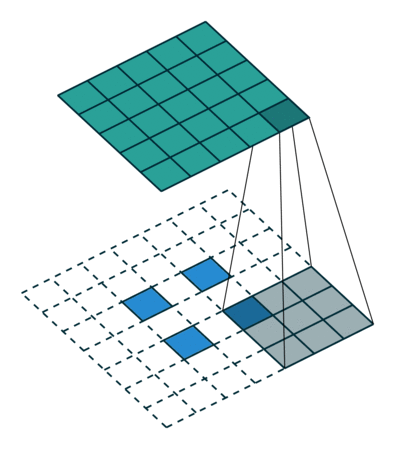
在这里插入图片描述

左边是stride=1（称为No Stride）的反卷积，右边是stride=2 的反卷积。可以看到，他们的区别就是在原始图片的像素点中间填充了0。没错，在反卷积中，stride参数就是表示往输入图片每两个像素点中间填充0，而填充的数量就是 stride - 1。

例如，我们对32x32的图片进行反卷积，stride=3，那么它就会在每两个像素点中间填充两个0，原始图片的大小就会变成 $32+31\times 2=94$ 。用代码实验一下：

inputs = torch.ones(1, 1, 32, 32)
transposed_conv = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=3, padding=2, stride=3, bias=False)
outputs = transposed_conv(inputs)
print(outputs.size())

torch.Size([1, 1, 92, 92])

我们来算一下，这里我使用了反卷积的Full Padding（相当于没有对原始图像的边缘进行padding），然后stride传了3，相当于在每两个像素点之间填充两个0，那么原始图像就会变成 94x94 的，然后kernal是3，所以最终的输出图片大小为 $94 - 3 + 1 = 92$ .

反卷积的output_padding参数

不知道你有没有发现，如果卷积和反卷积的参数一致，卷积会让 $A$ 尺寸变为 $B$ 尺寸，那么反卷积就会将 $B$ 尺寸变为 $A$ 尺寸。

举个例子：

inputs = torch.rand(1, 1, 32, 32)
outputs = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=18, padding=3, stride=1)(inputs)
outputs.size()

torch.Size([1, 1, 21, 21])

我们这里将32x32的图片通过卷积变为了 21x21。此时我们将卷积变为反卷积（参数不变），输入图片大小变为 21x21：

inputs = torch.rand(1, 1, 21, 21)
outputs = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=18, padding=3, stride=1)(inputs)
outputs.size()

torch.Size([1, 1, 32, 32])

看，反卷积将 21x21 的图片又变回了 32x32，这也就是为什么要叫反卷积。

但。。，真的是这样嘛，我们再看一个例子：

inputs = torch.rand(1, 1, 7, 7)
outputs = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=0, stride=2)(inputs)
outputs.size()

torch.Size([1, 1, 3, 3])

inputs = torch.rand(1, 1, 8, 8)
outputs = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=0, stride=2)(inputs)
outputs.size()

torch.Size([1, 1, 3, 3])

inputs = torch.rand(1, 1, 3, 3)
outputs = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=3, padding=0, stride=2)(inputs)
outputs.size()

torch.Size([1, 1, 7, 7])

上面我们对7x7和8x8的图片都使用卷积操作，他们最后结果都是3x3，这样反卷积就会存在歧义，而反卷积默认选择了转换为7x7。原因可以见下图：

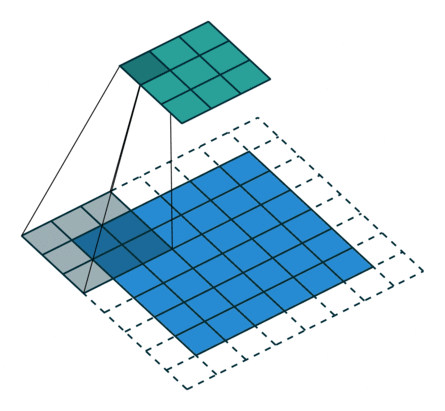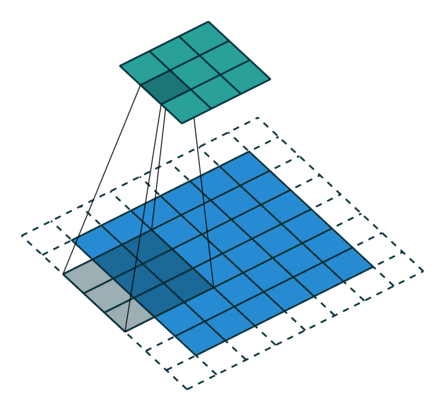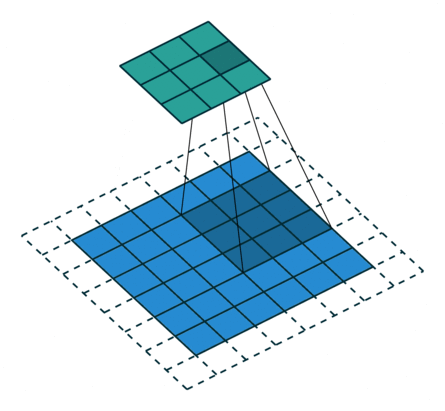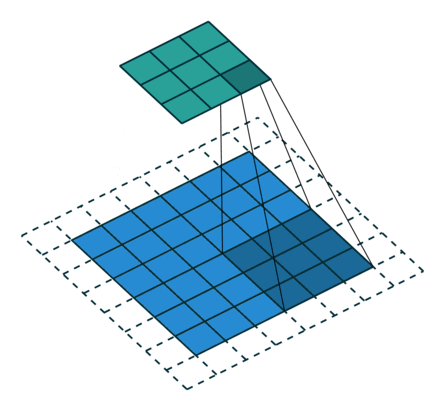
在这里插入图片描述

从这张图可以看到，8x8的图片其实最右边和最下边的一行是没有参与卷积运算的，这是因为stride为2，再走2步就超出图片范围了。所以7x7和8x8最终的结果都为3x3。

那么如果我们想让3x3的反卷积得8x8而不是7x7，那么我们就需要在输出图片边缘补充数据，具体补几行就是output_padding指定的。所以output_padding的作用就是：在输出图像右侧和下侧补值，用于弥补stride大于1带来的缺失。其中output_stadding必须小于stride

例如：

inputs = torch.rand(1, 1, 3, 3)
outputs = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=3, padding=0, stride=2, output_padding=1)(inputs)
outputs

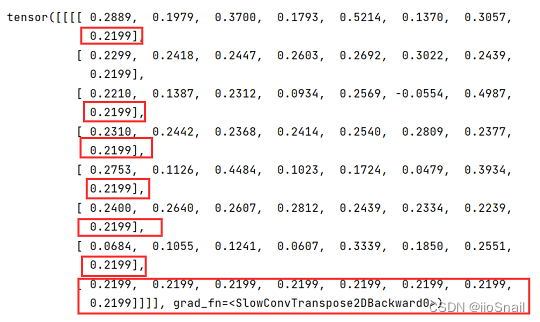
在这里插入图片描述

具体这个 0.2199 是什么我也不太清楚，我测试了发现并不是平均值

反卷积总结

反卷积的作用是将原始图像进行扩大
反卷积与传统卷积的区别不大，主要区别有：

2.1 padding的对应关系变了，反卷积的padding参数 $p^{'} = k - 1 - p$ 。其中 $k$ 是kernel_size, p为传统卷积的padding值；
2.2 stride参数的含义不一样，在反卷积中stride表示在输入图像中间填充0，每两个像素点之间填充的数量为 stride-1
2.3 除了上述的俩参数外，其他参数没啥区别
如果卷积和反卷积的参数一致，卷积会让 AA 尺寸变为 BB 尺寸，那么反卷积就会将 BB 尺寸变为 AA 尺寸
output_padding的作用就是：在输出图像右侧和下侧补值，用于弥补stride大于1带来的缺失。其中output_stadding必须小于stride