1.理解

计算属性:

1.定义:要用的属性不存在，要通过已有属性计算得来

2.原理:底层接住了Object.defineproperty方法提供的getter和setter

3.get函数什么时候执行？

• 初次读取会执行一次

• 当以来的数据发生变化时会被再次调用

  .

4.优势:与methods相比，内部有缓存机制(复用).效率更高

5.备注:

​ 1.计算属性最终会出现在vm上，直接读取即可

​ 2.如果计算属性要被修改，那必须写set函数去响应修改，且set中要引起计算时以来的数据发生变化

2.案例

假设1我们需要实现一个“填入姓和名,自动生成姓名”的效果,如下图

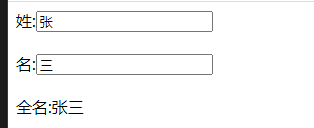
我们可以用修饰符**{{}}、methods、和计算属性computed**三种方式来实现这个案例

1.修饰符{{}}

优点:简单方便

缺点:对于复杂的表示式，会造成代码不简洁

​

<div id="app">姓:<input type="text" v-model="firstName"><br><br>名:<input type="text" v-model="lastName"><br><br>全名:{{firstName}}+{{lastName}}</div>

 const vm = new Vue({el:'#app',data:{firstName:'',lastName:'',}})

通过v-model双向绑定，我们可以在姓名输入框输入相应的值，全名使用通配符+表达式，实现全名的渲染

2.methods函数

优点:可以处理复杂的逻辑判断，代码量不会繁琐

缺点:与计算属性相比，函数可能会不必要的执行

<div id="app">姓:<input type="text" v-model="firstName"><br><br>名:<input type="text" v-model="lastName"><br><br>全名:{{showFullName()}}</div>

 const vm = new Vue({el:'#app',data:{firstName:'',lastName:'',},methods:{showFullName(){return this.firstName+'-'+this.lastName}}})

通过修饰符+函数，我们可以实现复杂的逻辑判断，函数内可以进行很多的操作

3.计算属性computed

优点:精准高效，可以准确的观测到数据的变化

 <div id="app">姓:<input type="text" v-model="firstName"><br><br>名:<input type="text" v-model="lastName"><br><br>全名:{{fullName}}</div>

const vm = new Vue({el:'#app',data:{firstName:'',lastName:'',},computed:{fullName:{get(){console.log('get被调用了');return this.firstName+'-'+this.lastName},set(value){const arr = value.split('-')this.firstName =arr[0]this.lastName = arr[1]}}}})

以上案例也可以实现，但是我们使用计算属性的优点是什么呢，我们为什么要选择用似乎更加麻烦的计算属性呢，我们先来看它的get函数

 get(){console.log('get被调用了');return this.firstName+'-'+this.lastName},

我们在之前就说到，计算属性含有缓存机制，也就是说，get函数只在初次读取fullName时或者所依赖的数据发生变化时，才进行调用

比方说

 <div id="app">姓:<input type="text" v-model="firstName"><br><br>名:<input type="text" v-model="lastName"><br><br>全名:{{fullName}}全名:{{fullName}}全名:{{fullName}}全名:{{fullName}}</div>

当我们多次调用fullName，那么我们的get函数会不会多次调用呢?

我们可以发现，当我们修改姓名的值时，get函数只执行了一次，这就是计算属性特有的缓存机制，即只有以下情况get才会调用,这样可以大大的提高执行效率

1.初次读取fullName

2.依赖的数据发生变化

我们再来看看set函数

当我们需要修改fullName的值时，我们需要set函数

set(value){console.log("set被调用了");const arr = value.split('-')this.firstName =arr[0]this.lastName = arr[1]}

我们先不使用set函数，看看我们是否可以修改fullName

当我们在控制台修改fullName的值时

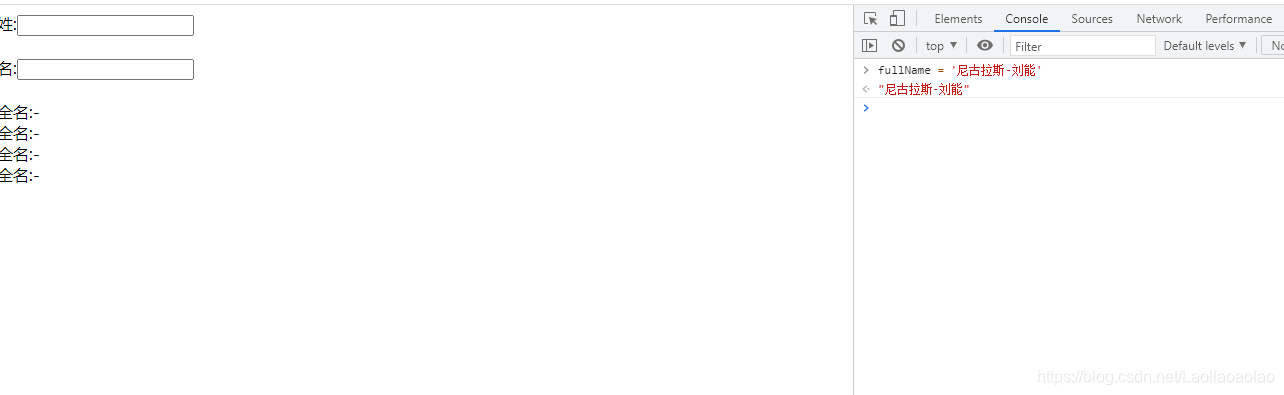
页面没有任何变化,这是为什么呢？

因为fullName其实是由firstName和lastName组合而成的，我们要想修改fullName，就必须修改firstName和lastName，而修改它们我们就要用到set函数

我们现在使用set函数并修改fullName的值

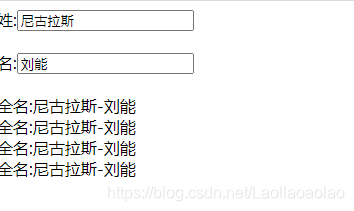
我们发现页面也响应的改变了，这就是计算属性中的set的用法

set什么时候调用呢？

当修改计算属性时，set函数就会被调用