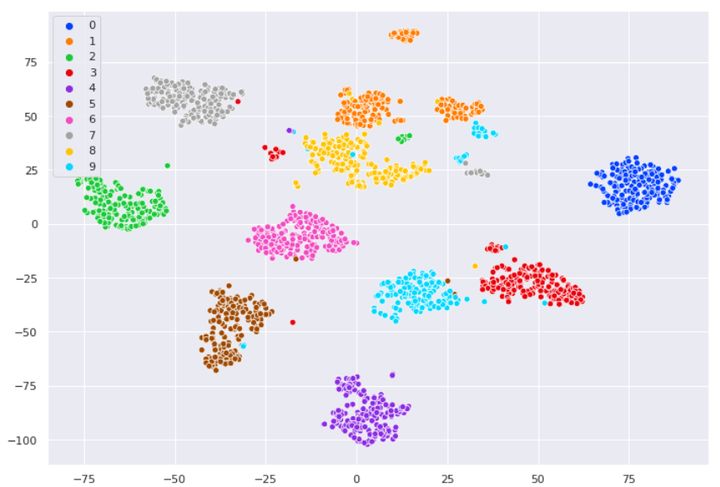
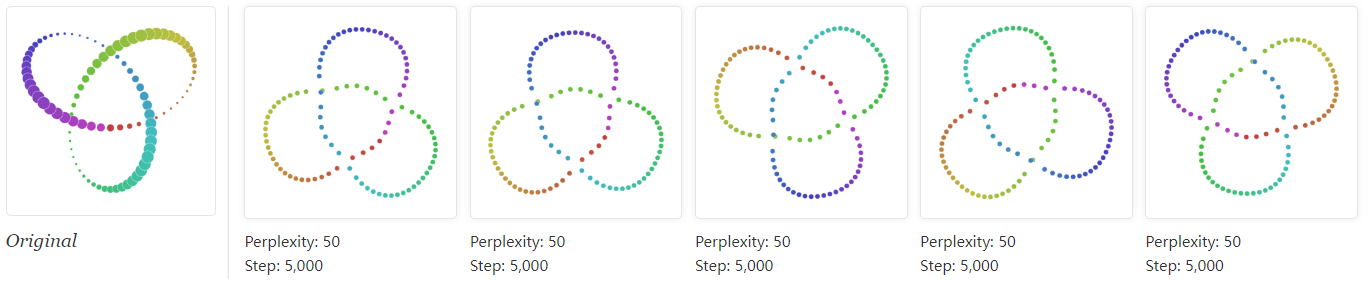
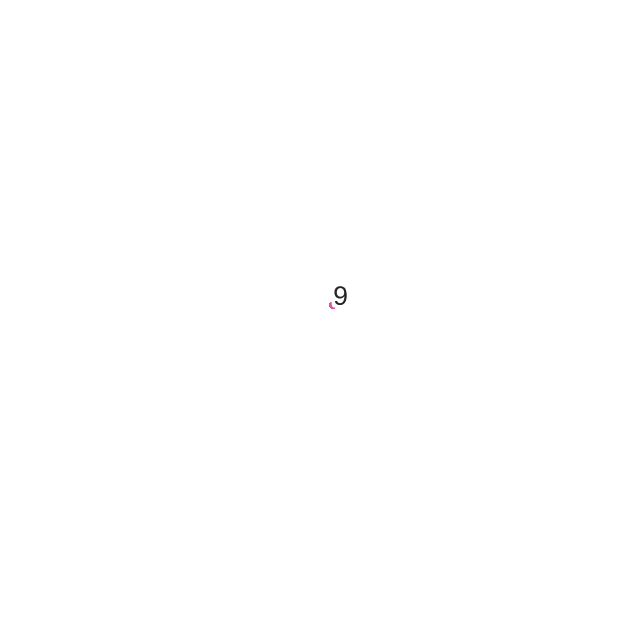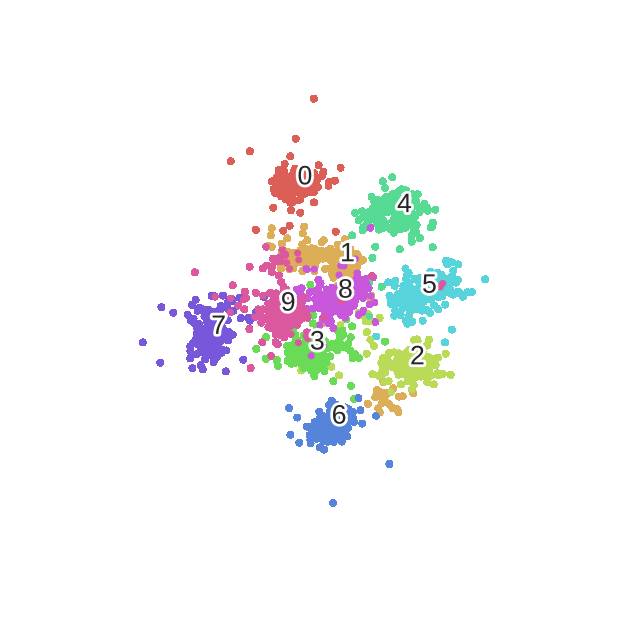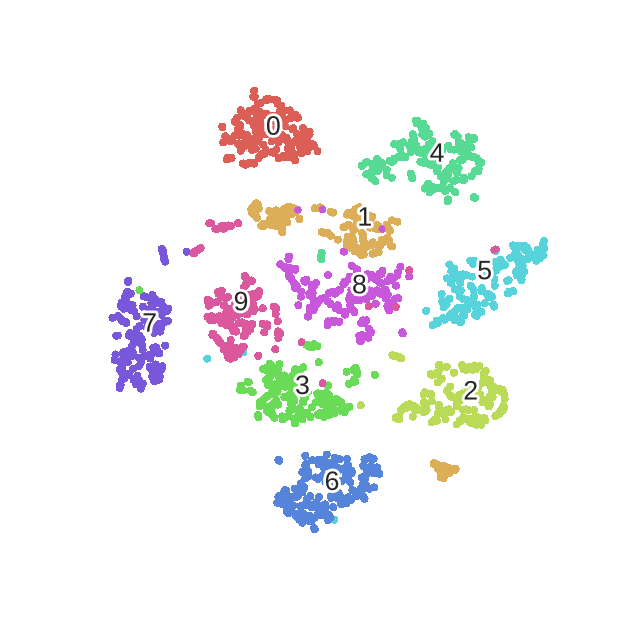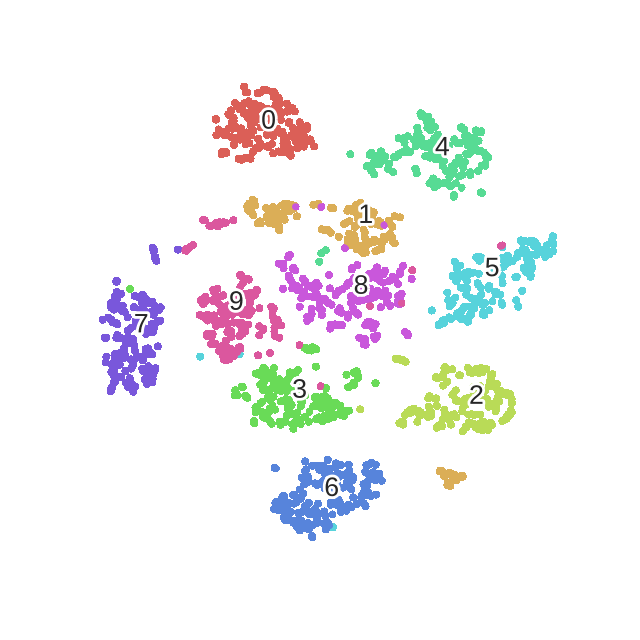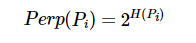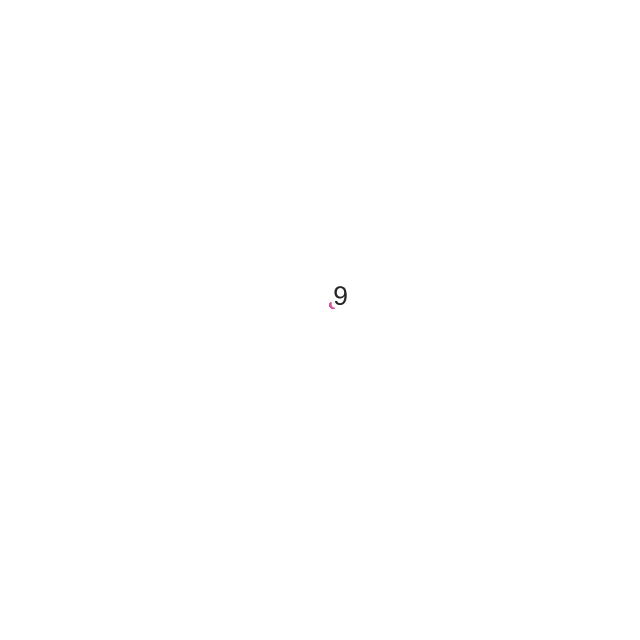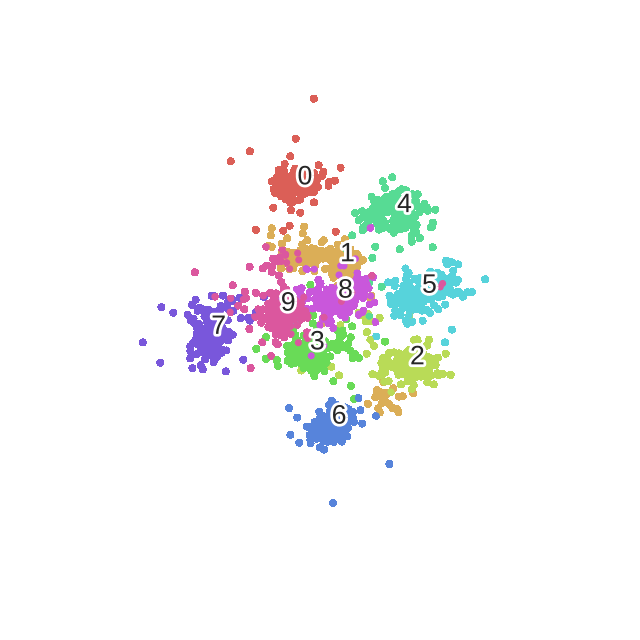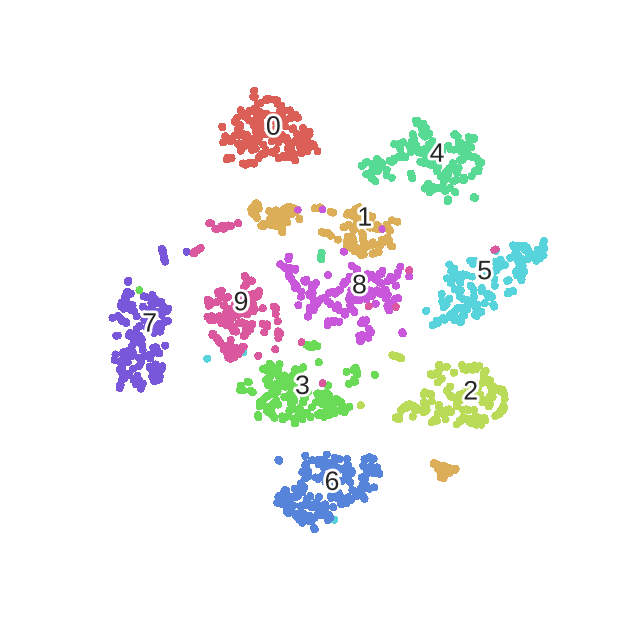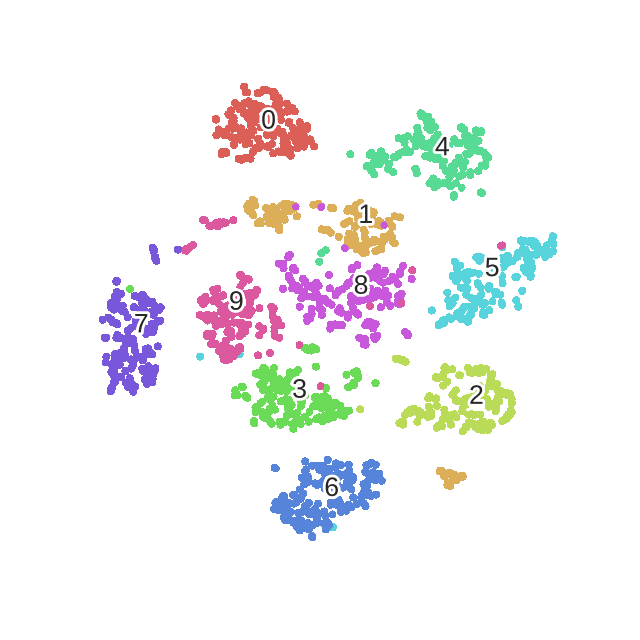本篇主要介绍很好的降维方法t-SNE的原理

详细介绍了困惑度perplexity对有效点的影响
首先介绍了SNE
然后在SNE的基础上进行改进：1.使用对称式。2.低维空间概率计算使用t分布

t-SNE（t分布和SNE的组合）

以前的方法有个问题：只考虑相近的点在降维后应该接近，但没有考虑不相近的点在降维后应该比较远
t-SNE主要原理为：

其中 $S(x^i , x^j)$ 代表 $x^i$ 与 $x^j$ 之间的相似度

SNE

原理：

在这里插入图片描述

这里可以看做高斯函数， ${||x_i - x_j||}^2$ 是自变量，也就是横坐标，高斯函数的值是纵坐标。方差越大，高斯函数越平滑，概率高的点就比较多。方差越小，函数越尖锐，概率大的点就比较少。可以认为，当我们在寻找一个点的邻近点时，方差可以调节我们寻找的主要邻近点的个数

在这里插入图片描述

特点

考虑计算原始空间中，其他所有点 j 与点 i 之间的距离，并转换为概率，代表相似程度
用指数，距离一拉开，相似度会迅速下降
我们的目标就是在目标空间中找其他所有点 j 与点 i 之间的距离，并转换为概率，且这个概率和原始空间的概率越接近越好
- 接近就代表着分布类似
- 保证了离得近的点还离得近，离得远的点还离得远
  - 这是该算法的很重要的优点
  - 以前的算法要么只考虑距离远的点还要距离远，要么只考虑距离近的点还要距离近
- 计算量很大，因为每个点都要算 P 和 Q

困惑度（perplexity）：

在这里插入图片描述

困惑度可以解释为有效邻居（其他点也考虑，只不过占比重太小了，不是有效邻居）的平滑方法
$H(P_i)$ 是 Shannon Entropy 。
- 用来解释混乱度，怎么理解混乱度呢？
  - 比如一个分类任务，将一个物体分为两个类
  - $-\sum(p_i)\log(p_i)$
  - 如果分为第一个类的概率 $p_1 = 1$ , 显然 $p_2 = 0$ , 这时的 $H = 0 + 0 = 0$ , 这时H小，意味着混乱度低，因为我们可以明确如何进行分类，所以不混乱
  - 如果分为第一个类的概率 $p_1 = 0.5$ , 显然 $p_2 = 0.5$ , 这时 $-(0.5\log0.5 \quad + \quad0.5\log0.5 = -\log0.5 )$ 这时， H的值达到最大。意味着混乱度高，因为我们无法确定如何分类
  - 对应到混乱度函数的图像中，就是 $p$ 的值越接近中间，混乱度越大，越接近两边，混乱度越小。
  - 上面我们讨论的是两个 $p$ 的情况，扩展到多个 $p$ 也一样。各个 $p$ 越靠近中间，混乱度越大（也就是 H 大）
- 如图，当 $p$ 分布在两端时，函数的值比较小。如果 $H$ 的值增大，则意味着，有更多的 $p$ 往中间分布了（左边的往右移动，右边的往左移动），也就是我们在大 $p$ 和小 $p$ 之间做了一个均衡，小的 $p$ 变大了，大的 $p$ 变小了，各个 $p$ 更接近了。这时候就代表着，我们在寻找一个点的邻近点时，考虑了更多的有效点（以前有些离得太远的点没有认定为有效点）
- 将 $p$ 的值放到下面的高斯函数图像中观察，这就对应 $\sigma$ 更大。也就是高斯分布更平滑了。因为，高斯分布越平滑，能获得比较大的值的点越多，也就是距离稍远的点也有不错的高斯函数值。这些点对应的 $p$ 也就变大了，对loss的影响也变大，成为有效点。

在这里插入图片描述
也就是说，我们可以通过调节困惑度 perplexity 来调节 H ，进而调节 $\sigma$

困惑度越大， H就越大， $\sigma$ 就越大，我们在寻找一个点的邻近点的时候就会考率更多的有效点
困惑度越大，越考虑全局（考虑的点更多，更远），困惑度越小，越考虑局部（考虑的点更少，更近）

评价标准：K-L散度

$C=\sum_{i} K L\left(P_{i} \| Q_{i}\right)=\sum_{i} \sum_{j} p_{j \mid i} \log \frac{p_{j \mid i}}{q_{j \mid i}}$

$p_{j|i}$ 越大， $q_{j|i}$ 越小时，此时的Cost越高。即高维空间的点越接近，映射到低维空间时反而越远，此时的惩罚是很大的，这是正确的情况。
$p_{j|i}$ 越小， $q_{j|i}$ 越大时，此时的Cost越小。即高维空间的点距离远时，映射到低维空间的点接近时，此时的惩罚却很小，这时跟我们想要的结果正好相反。
这个问题也是t-SNE的一个缺点。

因此SNE倾向于保留局部特征，即让高维离得近的点尽可能在低维时聚在一起，但是不考虑不同类间的间隔，直观理解为：整个降维后的图像会比较“拥挤”（原因就是上面这个，导致长程斥力不够）

t-SNE

优化：相较于SNE，有两方面优化：

优化了 p 和 q 的对称性
使用 t 分布优化了 q

对称性：

注意到，概率函数具有不对称性，即 $P_{i|j} \ne P_{j|i}$ 且 $Q_{i|j} \ne Q_{j|i}$ ，因为分母不一样。这与我们的直觉不符，无论 $x_i$ 和 $x_j$ 谁作为中心，其出现在对方附近的概率应该是相同的

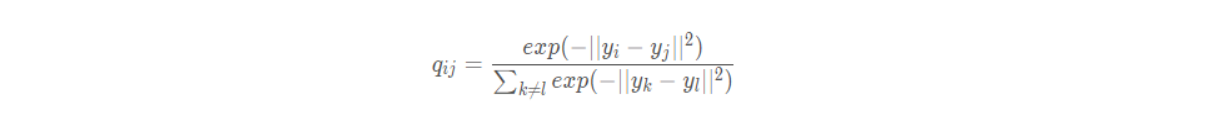
在这里插入图片描述

当然我们也可以在原空间（高维空间）中定义
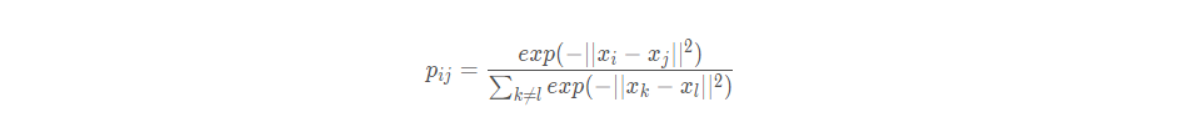
在这里插入图片描述

但是这样会带来问题：假设点 $x_i$ 是一个噪声点，那么 $x_i - x_j|$ 的平方会很大，那么对于所有的 j， $p_{ij}$ 的值都会很小，导致在低维映射下的 $y_i$ 对整个损失函数的影响很小，但对于异常值，我们显然需要得到一个更大的惩罚

于是我们定义： $p_{ij} = \frac{p_{i|j} + p_{j|i}}{2n}$

这样既保证了对称，又不会导致概率值像上面一样小(因为如果 $i$ 是噪声，那么 $P_{i|j}$ 就会比 $P_{j|i}$ 大得多)

t分布优化q

t分布优化后的q
$q_{i j}=\frac{\left(1+\left\|y_{i}-y_{j}\right\|^{2}\right)^{-1}}{\sum_{k \neq l}\left(1+\left\|y_{i}-y_{j}\right\|^{2}\right)^{-1}}$
梯度
$\frac{\delta C}{\delta y_{i}}=4 \sum_{j}\left(p_{i j}-q_{i j}\right)\left(y_{i}-y_{j}\right)\left(1+\left\|y_{i}-y_{j}\right\|^{2}\right)^{-1}$

当 $q_{ij}$ 太大或者太小时，也就是 $y_i - y_j)$ 太大或者太小，都会导致梯度趋近于0 ，这不利于更新点 $i$ 的坐标，这是目前的一个问题。不过一般情况下，这种情况出现比较少，而且其他点的的更新也会影响点 $i$ 的梯度
映射后的样本相似度采用 t-分布的一种，是对SNE的改进，这里改变的是 q ，且 q 已经经过对称优化了

在这里插入图片描述
横轴表示距离，纵轴表示相似度, 可以看到，对于较大相似度的点，t分布在低维空间中的距离需要稍小一点；而对于低相似度的点，t分布在低维空间中的距离需要更远。这恰好满足了我们的需求，即同一簇内的点(距离较近)聚合的更紧密，不同簇之间的点(距离较远)更加疏远。
一句话来说：因为我们的目的是令 $q_{ij}$ 与 $p_{ij}$ 相等。若达成这个目标，在低维空间中，近的点会更近，远的点会更远