普通莫队

莫队可以说是一个算法，但更多是一种思想。

我们先来看看普通莫队解决的问题：

有一个长度为 $n$ 的数列 $a$。
$q$ 个询问：$a$ 在 $[l_i,r_i]$ 中有多少个不同的数。
不强制在线。$1\le n,q\le 5\times 10^5$

遇到这种区间问题，第一个想法是前缀和，但很快会发现不可行。于是你搬出了树状数组，切了这道题（

但总有一些人觉得树状数组太难写了。

于是考虑其他做法。

如果目前知道了 $[l,r]$ 这个区间内的答案，你可以在 $O(1)$ 时间内求出 $[l-1,r],[l+1,r],[l,r-1],[l,r+1]$ 这些区间的答案。

具体操作是：

用一个数组 $b_i$ 记录当前区间 $[l,r]$ 中每个数字出现个数。
端点左移或右移后，区间会添加或减少一个数 $x$，让 $b_x$ 对应更改，判断 $b_x$ 是否从 $0$ 变成非 $0$ 或者从非 $0$ 变成 $0$。
如果有，就将这个区间内的答案对应加 $1$ 或减 $1$。

这样，通过若干次移动，我们可以从上一个询问 $[l_{i-1},r_{i-1}]$ 的答案，推出下一个询问 $[l_i,r_i]$ 的答案。但每次需要一定时间。

于是尝试能否通过前面询问答案快速推出后面询问答案。

将所有询问按照二元组 $(l,r)$ 排序，可能可以实现上面的要求。

但是时间复杂度是 $O(n^2)$ 的。

那么需要换一种排序方法：

先将询问按照左端点 $l$ 排序。
将数组分成 $\sqrt{n}$ 块，
最后对于 $l$ 在同一块内的询问，对于 $r$ 再重新排序。

其实这种排序方法简化就是：

将 $n$ 个询问分块。
对询问按以 $l$ 所属块编号升序为第一关键字，$r$ 升序为第二关键字的方式排序。

这时候可以证明当 $n,q$ 同阶时，时间复杂度是 $O(n\sqrt{n})$ 的。

块内，左端点每询问移动不超过 $\sqrt{n}$ 次。共有 $q$ 个询问。所以时间复杂度为 $O(n\sqrt{q})$
每块，计算一开始的答案时间复杂度 $O(n)$。共有 $\sqrt{n}$ 个块。所以时间复杂度为 $O(n\sqrt{n})$
每块，右端点移动不超过 $n$ 次。共有 $\sqrt{n}$ 个块。所以时间复杂度为 $O(n\sqrt{n})$

以上是普通莫队，莫队的最基础用法。

当然莫队还有各种变化和优化。

反复横跳奇偶优化

当我们在块间移动左右端点时，会发现需要移动很多次，导致时间暴增。

其中一部分原因是由于每块中右端点 $r$ 都是按照增序排序的。会导致每次需要从最右端移到最左端。

所以，理所当然的，对于第奇数个块，让右端点 $r$ 按照增序排序，对于第偶数个块，让右端点 $r$ 按照降序排序。

别看优化简单，但是作用非常大。

带修莫队

顾名思义，带修改的莫队。

例题：

有一个长度为 $n$ 的数组 $a$。
$q$ 个操作：

• 询问 $a$ 在 $[l,r]$ 中有多少个不同的数。
• 将 $a_i$ 替换成 $v$。

不强制在线。$1\le n,q\le 5\times 10^5$

这时只需加入一个时间戳，将询问变成 $(l,r,t)$ 即可

移动操作自然变成了六种。

排序方法则是

把数组分成 $\sqrt[4]{n^{3}t}$ 块
以左端点所在块为第一关键字，右端点所在块为第二关键字，时间戳为第三关键字，升序排序。

为什么不是 $\sqrt{n}$ 呢？有一位大佬证明过这种情况下 $\sqrt[4]{n^{3}t}$ 是最优的。

然后每次就按顺序移动左右端点和时间戳计算答案即可。

树上莫队

数组上的莫队我知道，但树上莫队是干啥的？

路径问题

有一棵 $n$ 个节点树，每个节点有一个值 $a$。
$q$ 个询问，每次询问节点 $u$ 到节点 $v$ 之间路径上有多少不同值。
不强制在线。$1\le n,q\le 10^5$

可以想到，如果我们把每个询问表示成 $(u,v)$，那么是可以从一个询问的答案 $O(1)$ 推到另一个询问的答案的。

但是，问题来了，怎么排序？我们并不知道如何排序才能保证时间复杂度。

所以最终还是需要回归数组。

尝试将这棵树的信息用数组储存，并且这个数组满足一个区间的答案可以 $O(1)$ 推到另一个区间的答案。

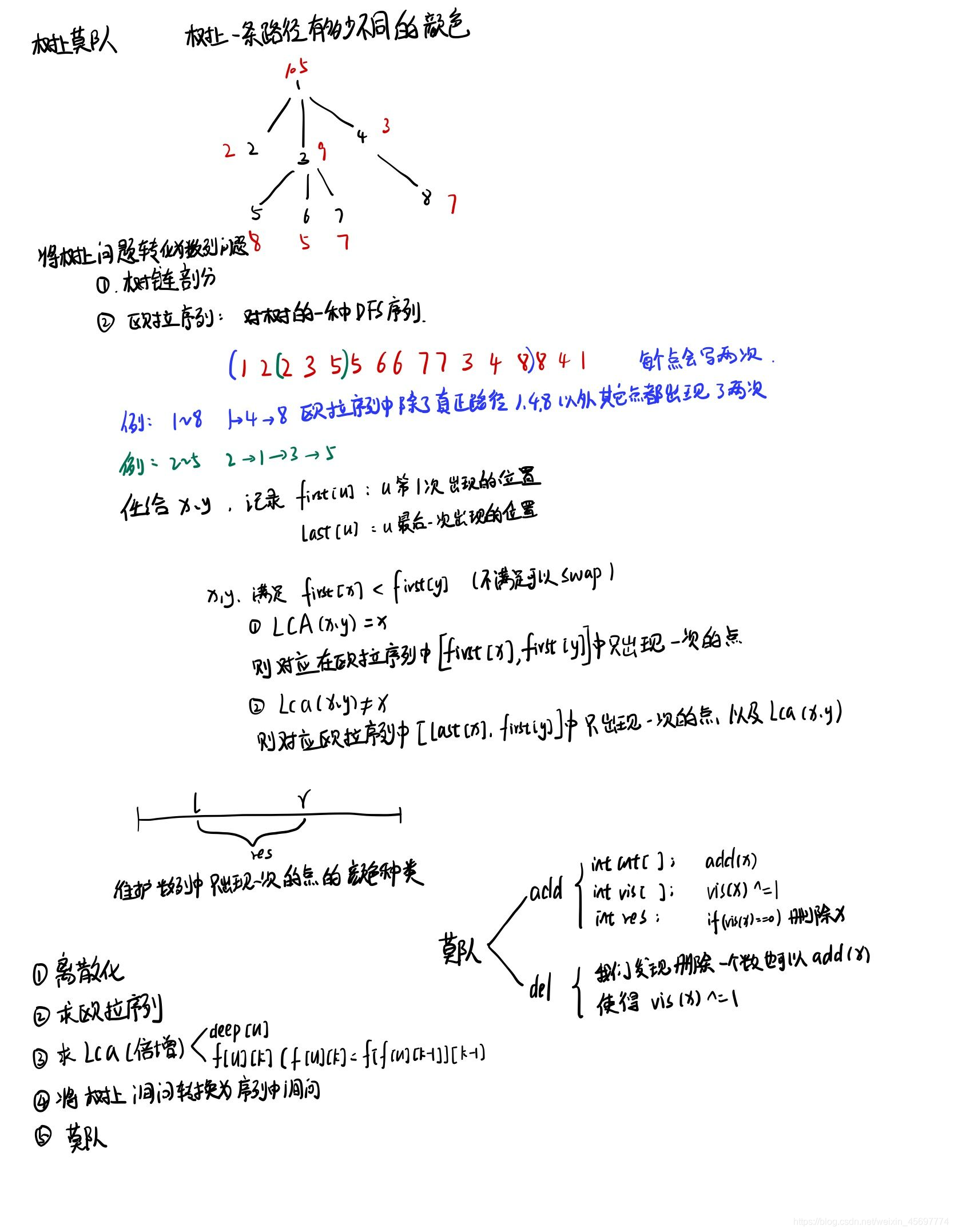
这时就需要用到欧拉序了。（欧拉序就是在 $dfs$ 的时候进入和离开一个节点都将节点记录后形成的序列）

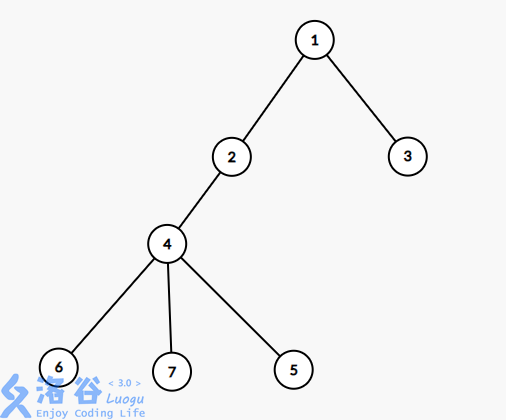
首先将这棵树的欧拉序用 $dfs$ 跑出来。

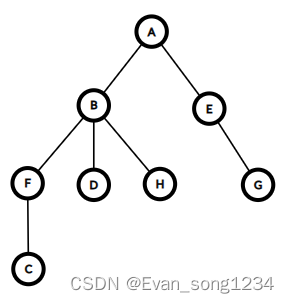
如图，这棵树的欧拉序为 $ABFCCFDDHHBEGGEA$，我们记录下每个节点前后两次出现的位置 $L_i$ 和 $R_i$。

现在要做的就是把每个询问的 $[u,v]$ 转到欧拉序上的一个区间 $[l,r]$。

可以发现，如果把欧拉序上一个区间 $[l,r]$ 内所有出现两次的点删除，则剩余的点可以组成一个路径。

尝试从路径推出区间，分成路径两种情况：

1. 路径首尾节点为祖先关系。则相当于区间 $[L_u,L_v]$ 或 $[R_v,R_u]$。
2. 路径首尾节点不为祖先关系。则相当于区间 $[R_u,L_v]+lca(u,v)$ 或 $[R_v,L_u]+lca(u,v)$。

将所有路径转换为区间，就可以使用普通莫队解决问题了。

子树问题

有一棵 $n$ 个节点树，每个节点有一个值 $a$。
$q$ 个询问，每次询问节点 $u$ 的子树上有多少不同值。
不强制在线。$1\le n,q\le 10^5$

同样，还是考虑如何把树上问题转换成区间问题。

显然，我们只需要用 $dfs$ 序标记节点，即可使每个子树节点编号连续。

而且这还不需要分类讨论。

回滚莫队

有一个长度为 $n$ 的数组 $a$。设 $cn{t}_{i,l,r}$ 为在 $[l,r]$ 区间内 $i$ 的出现次数。
$q$ 次询问，询问 $[l_i,r_i]$ 区间内最大的 $cn{t}_{j,l_i,r_i}\times j$。
不强制在线。$1\le n,q\le 10^5$

我们先按照普通莫队的思路来思考。

首先，考虑区间端点能否快速移动。

若 $[l,r]$ 区间右端点 $r$ 向右移动或左端点 $l$ 向左移动，我们只需把新增的数的出现次数乘上自己后与最大值取 $max$ 即可。

但如果是左端点 $l$ 右移，右端点 $r$ 左移呢？我们发现难以 $O(1)$ 解决。

怎么办？

我们干脆不左端点不左移，右端点也不右移了。

排序还是按照原来的方法：

将 $n$ 个询问分块。
对询问按以 $l$ 所属块编号升序为第一关键字，$r$ 升序为第二关键字的方式排序。

然后过程有所改变：

设当前询问所在块左端点为 $s_i$，右端点为 $t_i$。
每块初始化：

1. 我们将莫队区间 $[l,r]$ 的左端点 $l$ 重置到 $t_i+1$，右端点重置到 $t_i$，此时莫队区间为空。

回答块内询问：

1. 如果莫队区间右端点在询问右端点右边，则代表询问左端点和右端点处于同一块内，直接暴力计算。
2. 将莫队区间右端点 $r$ 移动到询问右端点。
3. 记录下当前莫队区间答案。
4. 将莫队区间左端点 $l$ 移动到询问左端点。
5. 回答询问。
6. 使用先前记录的答案重置莫队区间，使左端点 $l$ 回到 $t_i+1$。