随机变量
随机变量定义:
样本空间为Ω,随机变量X表示样本空间Ω中的一个样本点(样本空间和随机变量的关系类似于实数轴上的x轴和自变量x的区别)。如随机抛掷一枚骰子,X就是表示骰子的点数。
分布函数
分布函数定义:
F(X)=P(X<=x)
离散型随机变量的分布函数:
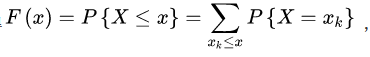
连续性随机变量的分布函数:
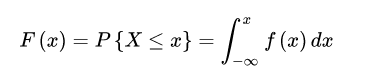
分布函数的性质:
1.非降性
F(x)是一个非递减函数
2.归一性
在x趋向于+∞时,F(x)趋向于1
3右连续性
因为 F(x)是单调有界非减函数,所以其任一点x0的右极限F(x0+0)必存在。
数学期望
在概率论和统计学中,数学期望(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
离散型随机变量的期望:
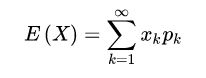
连续型随机变量的期望:
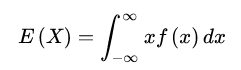
性质:
1.E©=C
2.E(CX)=CE(X)
3.E(X+Y)=E(X)+E(Y)
4.当X和Y相互独立时,E(XY)=E(x)E(y)
方差
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
D(x)=E ( ( X-E( X ) )2)
离散型变量的方差:
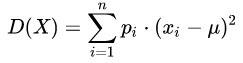
随机型变量的方差:
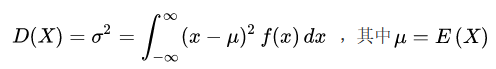
展开上式可得:
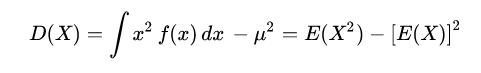
性质L:
D©=0
D(CX)=C2D(X)
D(X±Y)=D(X)+D(Y)±2E( (X-E(X))*(Y-E(Y)) )
若X,Y相互独立,则D(X±Y)=D(X)+D(Y)
离散型随机变量三大常见分布:
1.两点分布(伯努利分布)
定义:
一个非常简单只有两个可能结果的试验,比如正面或反面,成功或失败,有缺陷或没有缺陷,病人康复或未康复。记为X~(0,1)
分布律:
| X | 0 | 1 |
|---|---|---|
| P | (1-p) | p |
性质:
期望E(X)=p
方差D(X)=p(1-p)
2.二项分布
定义:
在n次独立重复的伯努利试验中,设每次试验中事件A发生的概率为p。用X表示n重伯努利试验中事件A发生的次数,则X的可能取值为0,1,…,n,且对每一个k(0≤k≤n),事件{X=k}即为“n次试验中事件A恰好发生k次”,随机变量X的离散概率分布即为二项分布。
可以简单理解为多次抛硬币事件的概率分布。
记做X~b(n,p)
分布律:
| X | 0 | 1 | 。。。 | k |
|---|---|---|---|---|
| P | C0p0(1-p)(n) | C1p1(1-p)(n-1) | 。。。 | Ckpk(1-p)(n-k) |
性质:
期望E(X)=np
方差D(X)=np(1-p)
就是在两点分布的基础上乘以一个n
泊松分布:
定义:
二项分布的近似解,当n非常大,p非常小,计算十分复杂时,可以用泊松公式求近似解。(n>200,p<0.05) 记做X~P(λ)
概率函数:
λ表示数学期望,即np
k表示事件发生的次数
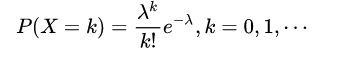
性质:
期望E(X)=λ=np
方差D(X)=λ
均匀分布
定义:
均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数a和b定义,它们是数轴上的最小值和最大值,通常缩写为X~U(a,b)。
概率密度函数:
a表示区间上界,b表示区间下界
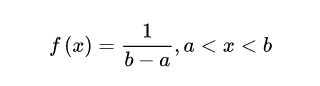
性质:
期望E(X)=(a+b)/2
方差D(X)=(b-a)2/12
指数分布:
定义:
指数分布(也称为负指数分布)是描述泊松过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况。 它是几何分布的连续模拟,它具有无记忆的关键性质。 除了用于分析泊松过程外,还可以在其他各种环境中找到。记做X~ E(λ)
概率密度函数:
λ表示期望的倒数
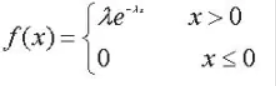
性质
期望E(X)=1/λ
方差D(X)=1/λ2
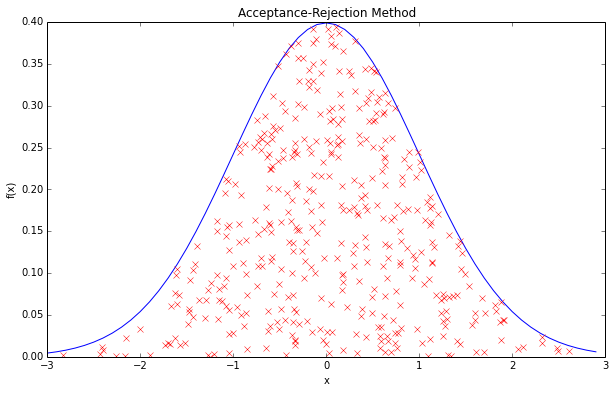
正态分布(高斯分布)
定义:
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为X~N(μ,σ2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
概率密度函数:
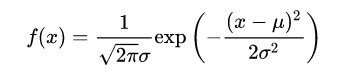
标准化:
将Y化为x的形式,转换为标准正态分布,方便查表计算。也可以用来算μ和σ。
F((96-0.5)/σ)=0.05,查表的到(96-0.5)/σ=2,可以求得σ。
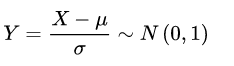
性质
期望E(X)=μ
方差D(X)=σ2
到这里概率论的基础就完结了,开始上数理统计部分了。概率论对深度学习帮助挺大的,主要是帮助理解概念,方便搭建更优化的神经网络。