生成随机数是程序设计里常见的需求。一般的编程语言都会自带一个随机数生成函数，用于生成服从均匀分布的随机数。不过有时需要生成服从其它分布的随机数，例如高斯分布或指数分布等。有些编程语言已经有比较完善的实现，例如Python的NumPy。这篇文章介绍如何通过均匀分布随机数生成函数生成符合特定概率分布的随机数，主要介绍Inverse Ttransform和Acceptance-Rejection两种基础算法以及一些相关的衍生方法。下文我们均假设已经拥有一个可以生成0到1之间均匀分布的随机数生成函数，关于如何生成均匀分布等更底层的随机数生成理论，请参考其它资料，本文不做讨论。

• 基础算法
  • Inverse Transform Method
    • ITM算法描述
    • ITM算法说明
    • ITM实现示例
  • Acceptance-Rejection Method
    • ARM算法描述
    • ARM算法说明
    • ARM实现示例
• 衍生算法
  • 组合算法
  • 生成具有相关性的随机数
• 更多参考

基础算法

Inverse Transform Method

最简单的生成算法是Inverse Transform Method（下文简称ITM）。如果我们可以给出概率分布的累积分布函数（下文简称CDF）及其逆函数的解析表达式，则可以非常简单便捷的生成指定分布随机数。

ITM算法描述

1. 生成一个服从均匀分布的随机数U∼Uni(0,1)
2. 设F(X)为指定分布的CDF，F−1(Y)是其逆函数。返回X=F−1(U)作为结果

ITM算法说明

这是一个非常简洁高效的算法，下面说明其原理及正确性。

我们通过图示可以更直观的明白算法的原理。下图是某概率分布的CDF：

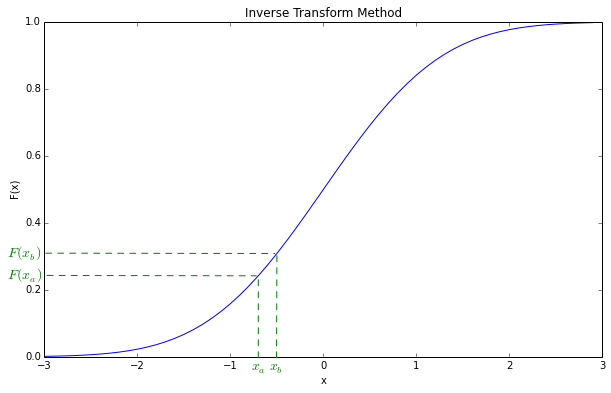
我们从横轴上标注两点xa和xb，其CDF值分别为F(xa)和F(xb)。

由于U服从0到1之间的均匀分布，因此对于一次U的取样，U落入F(xa)和F(xb)之间的概率为:

P(U∈(F(xa),F(xb)))=F(xb)−F(xa)

而由于CDF都是单调非减函数，因此这个概率同时等于X落入xa和xb之间的概率，即：

P(U∈(F(xa),F(xb)))=P(F−1(U)∈(F−1(F(xa)),F−1(F(xb))))=P(X∈(xa,xb))=F(xb)−F(xa)

而根据CDF的定义，这刚好说明X服从以F(x)为CDF的分布，因此我们的生成算法是正确的。

ITM实现示例

下面以指数分布为例说明如何应用ITM。

首先我们需要求解CDF的逆函数。我们知道指数分布的CDF为

F(X)=1−e−λX

通过简单的代数运算，可以得到其逆函数为

F−1(Y)=−1λln(1−Y)

由于U服从从0到1的均匀分布蕴含着1−U服从同样的分布，因此在实际实现时可以用Y代替1−Y，得到：

F−1(Y)=−1λln(Y)

下面给出一个Python的实现示例程序。

import random
import math
def exponential_rand(lam):
    if lam <= 0:
        return -1
    U = random.uniform(0.0, 1.0)
    return (-1.0 / lam) * math.log(U)

Acceptance-Rejection Method

一般来说ITM是一种很好的算法，简单且高效，如果可以使用的话，是第一选择。但是ITM有自身的局限性，就是要求必须能给出CDF逆函数的解析表达式，有些时候要做到这点比较困难，这限制了ITM的适用范围。

当无法给出CDF逆函数的解析表达式时，Acceptance-Rejection Method（下文简称ARM）是另外的选择。ARM的适用范围比ITM要大，只要给出概率密度函数（下文简称PDF）的解析表达式即可，而大多数常用分布的PDF是可以查到的。

ARM算法描述

1. 设PDF为f(x)。首先生成一个均匀分布随机数X∼Uni(xmin,xmax)
2. 独立的生成另一个均匀分布随机数Y∼Uni(ymin,ymax)
3. 如果Y≤f(X)，则返回X，否则回到第1步

ARM算法说明

通过一幅图可以清楚的看到ARM的工作原理。

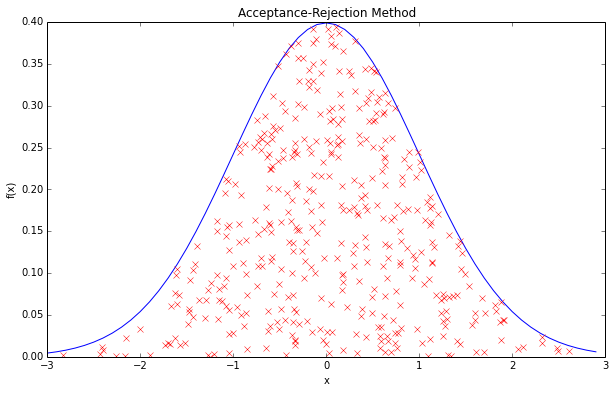
ARM本质上是一种模拟方法，而非直接数学方法。它每次生成新的随机数后，通过另一个随机数来保证其被接受概率服从指定的PDF。

显然ARM从效率上不如ITM，但是其适应性更广，在无法得到CDF的逆函数时，ARM是不错的选择。

ARM实现示例

下面使用ARM实现一个能产生标准正态分布的随机数生成函数。

首先我们要得到标准正态分布的PDF，其数学表示为：

f(x)=1√2πe−x22

为了方便，这里我会直接使用SciPy来计算其PDF。

程序如下。

import random
import scipy.stats as ss
 
def standard_normal_rand():
    while True:
        X = random.uniform(-3.0,3.0)
        Y = random.uniform(0.0, 0.5)
        if Y < ss.norm.pdf(X):
            return X

注意：标准正态分布的x取值范围从理论上说是(−∞,∞)，但是当离开均值点很远后，其概率密度可忽略不计。这里只取(−3.0,3.0)，实际使用时可以根据具体需要扩大这个取值范围。

衍生算法

组合算法

当目标分布可以用其它分布经过四则运算表示时，可以使用组合算法生成对应随机数。

最常见的就是某分布可以表示成多个独立同分布（下文简称IID）随机变量之和。例如二项分布可以表示成多个0-1分布之和，Erlang分布可以由多个IID的指数分布得出。

以Erlang分布为例说明如何生成这类随机数。

设X1,X2,⋯,Xk为服从0到1均匀分布的IID随机数，则−1λlnX1,−1λlnX2,⋯,−1λlnXk为服从指数分布的IID随机数，因此

X=−1λlnX1−1λlnX2−⋯−1λlnXk=−1λlnk∏i=1Xi∼Erl(k,λ)

所以生成Erlang分布随机数的算法如下：

1. 生成X1,X2,⋯,Xk∼Uni(0,1)
2. 返回−1λln∏ki=1Xi

这类分布的随机数生成算法很直观，就是先生成相关的n个IID随机数，然后带入简单求和公式或其它四则公式得出最终随机数。其数学理论基础是卷积理论，稍微有些复杂，这里不再讨论，有兴趣的同学可以查阅相关资料。

生成具有相关性的随机数

现在考虑生成多维随机数，以最简单的二维随机数为例。

如果两个维度的随机数是相互独立的，那么只要分别生成两个列就可以了。但是如果要求两列具有一定的相关系数，则需要做一些特殊处理。

下列算法可以生成两列具有相关系数ρ的随机数。

1. 生成IID随机变量X和Y
2. 计算X′=ρX+√1−ρ2Y
3. 返回(X,X′)

可以这样验证其正确性：

corr(X,X′)=ρcorr(X,X)+√1−ρ2corr(X,Y)=ρ

注意：corr(X,X)=1，corr(X,Y)=0。

因此X和X′确实具有相关系数ρ。

更多参考

这篇文章讨论了生成指定分布随机数的基本方法。这篇文章只打算讨论基础方法，所以还有很多有趣的内容，本文没有深入的探讨。这里给出一些扩展阅读资料，供有兴趣的朋友深入学习。首先是一篇非常好的文档，这篇文章来自美国陆军实验室，对计算机生成指定分布随机数的方方面面进行了全面深入描述，是不可多得的好资料。

在实现方面，可以参考NumPy中关于random的实现以及我开发的JavaScript实现。另外我做过一个不同概率分布的可视化页面，可以帮助你直观理解不同分布及PDF参数对分布的影响。