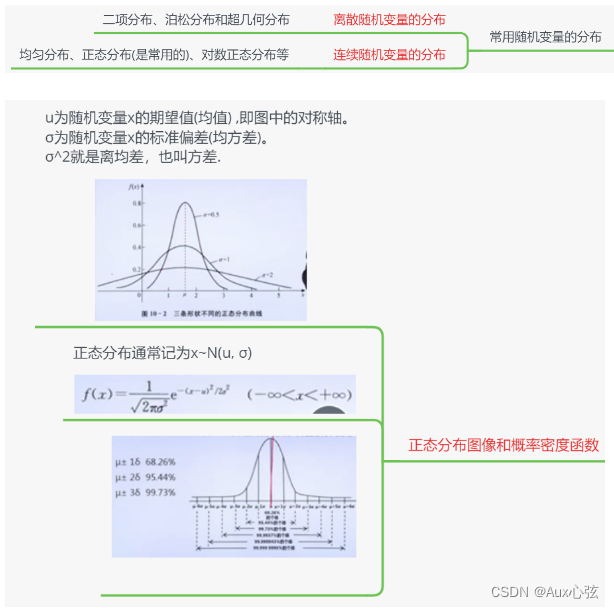
N.1 随机变量分布
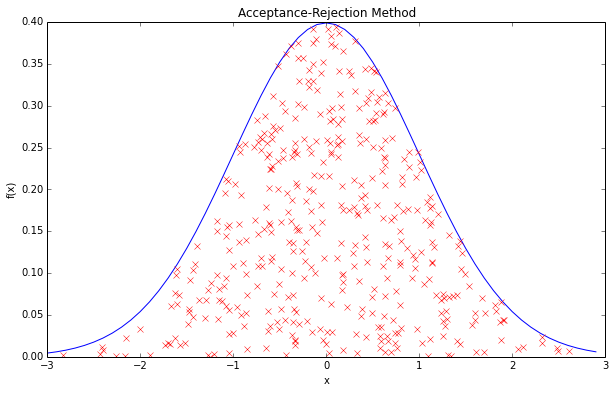
| 1)正态分布(高斯分布,用的比较多) 这里句一个例子,小明有一枚筛子,但它不是六个面的,而是数不清多的面(即每一面都有个点对应点数),但塞子的外形不均匀的,所以扔筛子有些点数的概率可能会大点。于是小明最中测试无数次,发现存在如下的公式关系。 |
————————————————————————

————————————————————————
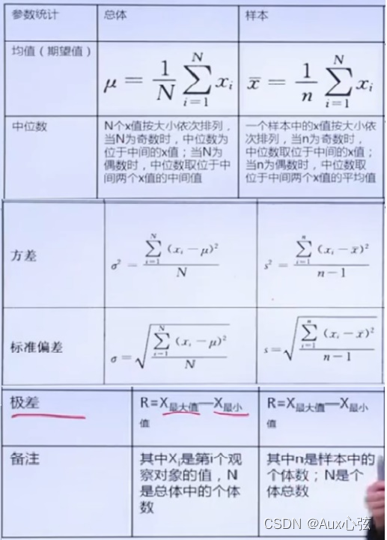
| 发现u出现做的点数(即概率最大的点数)。当然如果概率图不是左右对称的函数,那么u就可能“不是中位点数”。如果图形左右对称,那就说明是”中位点数”。 |
————————————————————————
————————————————————————
————————————————————————
| 2)指数分布 |
————————————————————————

————————————————————————
N.2 重要概率公式
| 1)条件概率公式 指A发生的情况前提下,B发生发概率,即AB同时发生。 |
————————————————————————
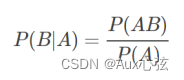
————————————————————————
| 2)全概率公式 这个是分类又分步计算。 |
————————————————————————
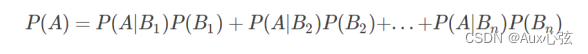
————————————————————————
| 3)贝叶斯公式 这个和条件概率公式一样,只是反过来计算。 |
————————————————————————
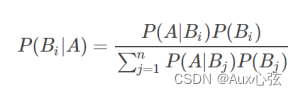
————————————————————————