常见的概率分布并生成随机数

article/2025/11/10 19:25:28

一、均匀分布（Uniform Distribution）

在相同长度间隔的分布概率是等可能的。

1.概率密度函数：

$f(x)=\left\{ \begin{matrix} \frac{1}{b-a} & a\le x\le b \\ 0 & else \\ \end{matrix} \right\}$

2.分布函数：

$F(x)=\left\{ \begin{matrix} 0 & x<a \\ \frac{x-a}{b-a} & a\le x\le b \\ 1 & x>b \\ \end{matrix} \right\}$

3.期望和方差：

$E(x)=\frac{a+b}{2};D(x)=\frac{{{(a-b)}^{2}}}{12}$

4.生成随机数

import numpy as np
#生成从0-1的均匀分布
np.random.rand(10)#生成十个均匀分布的随机数
np.random.rand(2，4)#生成八个均匀分布的随机数，维度2*4
#均匀分布
np.random.uniform(low=1, high=2,size=(2,4))#生成从1-2的均匀分布，维度2*4

二、正态分布（Normal Distribution）

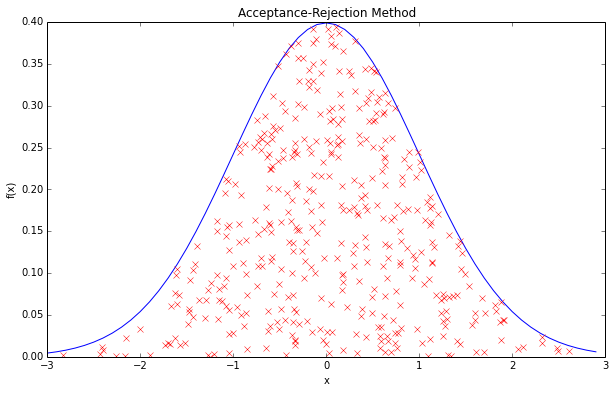
正态分布是具有两个参数μ和σ2的连续型随机变量的分布

1.概率密度函数：

$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{{e}^{-\frac{{{(x-\mu )}^{2}}}{2{{\sigma }^{2}}}}}$

2.分布函数：

是概率密度函数的积分

3.期望和方差：

$E(x)=\mu;D(x)=\sigma ^2$

4.生成随机数

import numpy as np
#标准正态分布
np.random.randn(10)#生成十个标准正态分布的随机数
np.random.randn(2，4)#生成十个均匀分布的随机数，维度2*4
#正态分布
np.random.normal(loc=0, scale=1, size=(2,4))#均值loc，方差是scale，维度是size

三、泊松分布（Poisson Distribution）

是一种典型的离散概率分布，参数λ表示单位时间（面积）内（随机事件的平均发生次数。当 $\lambda>20$ ,可以近似为正态分布

1.概率密度函数：

$P(X=k)=\frac{{{\lambda }^{k}}}{k!}{{e}^{-\lambda }},k=0,1,...$

2.期望和方差：

$E(x)=\lambda;D(x)=\lambda$

3.生成随机数

import numpy as np
#生成lambda = 10的泊松分布，维度为2*4
np.random.poisson(lam=10, size=(2,4))

四、贝塔分布（Beta Distribution)

作为伯努利分布和二项式分布的共轭先验分布的密度函数。通俗来说可以吧贝塔分布看作一个概率的概率分布，也就是当你不知道一个东西的具体概率是多少时，它可以给出所有概率出现的可能性大小。

1.概率密度函数

$f(x;\alpha ,\beta )=\frac{1}{B(\alpha ,\beta )}{{x}^{\alpha -1}}{{(1-x)}^{\beta -1}}$

2.分布函数：

$F(x;\alpha ,\beta )=\frac{{{B}_{x}}(\alpha ,\beta )}{B\left( \alpha ,\beta \right)}={{I}_{x}}(\alpha ,\beta )$

3.期望和方差：

$E(X)=\frac{\alpha }{\alpha +\beta };D(X)=\frac{\alpha \beta }{{{(\alpha +\beta )}^{2}}(\alpha +\beta +1)}$

4.生成随机数

import numpy as npnp.random.beta(a=3,b=5,size=(2,4))

五、指数分布（Beta Distribution)

描述泊松过程中的事件之间时间的概率分布

1.概率密度函数

$f(x)=\left\{ \begin{matrix} \lambda {{e}^{-\lambda x}} & x>0 \\ 0 & x\le 0 \\ \end{matrix} \right\}$

2.分布函数：

$F(x;\lambda )=\left\{ \begin{matrix} 1-{{e}^{-\lambda x}} & x\ge 0 \\ 0 & x<0 \\ \end{matrix} \right\}$

3.期望和方差：

$E(x)=\frac{1}{\lambda };D(x)=\frac{1}{{{\lambda }^{2}}}$

4.生成随机数

import numpy as npnp.random.exponential(scale = 2,size=(2,4))

六、瑞利分布（Rayleigh Distribution)

用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型

1.概率密度函数

$f(z)=\frac{z}{{{\sigma }^{2}}}{{e}^{-\frac{{{z}^{2}}}{2{{\sigma }^{2}}}}},z\ge 0$

2.期望和方差：

$E(x)=\sigma \sqrt{\frac{\pi }{2}}\approx 1.25\sigma ;D(x)=\frac{4-\pi }{2}{{\sigma }^{2}}\approx 0.43{{\sigma }^{2}}$

3.生成随机数

import numpy as np
#rayleigh([scale, size])
np.random.rayleigh(scale = 2,size=(2,4))