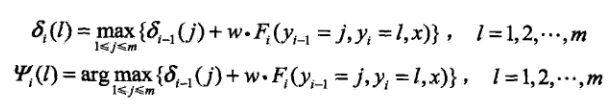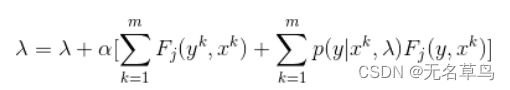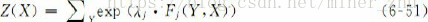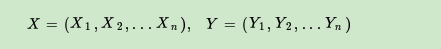1. 引言
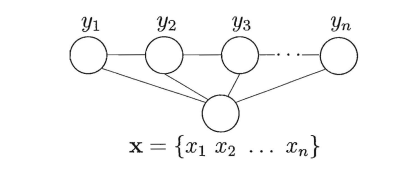
条件随机场,conditional random field,CRF,是给定一组输入随机变量的条件下,输出随机变量的条件概率分布模型。
条件随机场和隐马尔可夫模型的联系:
可以看到,条件随机场是一种无向图。
2. 概率无向图
概率无向图模型,又称马尔科夫随机场,是一个由无向图表示的联合概率分布。
- 成对马尔可夫性
设 u , v u,v u,v是无向图G中没有边连接的结点,对应的随机变量为 Y u , Y v Y_u, Y_v Yu,Yv. 其他结点为 Y O Y_O YO.
P ( Y u , Y v ∣ Y o ) = P ( Y u ∣ Y O ) P ( Y v ∣ Y o ) P\left(Y_{u}, Y_{v} | Y_{o}\right)=P\left(Y_{u} | Y_{O}\right) P\left(Y_{v} | Y_{o}\right) P(Yu,Yv∣Yo)=P(Yu∣YO)P(Yv∣Yo)
- 局部马尔可夫性
设 W W W是与 v v v有边连接的所有结点。
P ( Y v , Y o ∣ Y W ) = P ( Y v ∣ Y W ) P ( Y O ∣ Y W ) P\left(Y_{v}, Y_{o} | Y_{W}\right)=P\left(Y_{v} | Y_{W}\right) P\left(Y_{O} | Y_{W}\right) P(Yv,Yo∣YW)=P(Yv∣YW)P(YO∣YW)
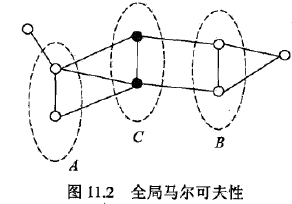
- 全局马尔科夫性
设结点集合 A , B A,B A,B是在无向图G中被结点集合 C C C分开的任意结点集合。
P ( Y A , Y B ∣ Y C ) = P ( Y A ∣ Y C ) P ( Y B ∣ Y C ) P\left(Y_{A}, Y_{B} | Y_{C}\right)=P\left(Y_{A} | Y_{C}\right) P\left(Y_{B} | Y_{C}\right) P(YA,YB∣YC)=P(YA∣YC)P(YB∣YC)
-
团:任意两结点均有边连接的结点子集。
-
最大团:不能再加入任一结点组成更大的团。
-
势函数, Ψ C Ψ_C ΨC函数
Ψ c ( Y c ) = exp { − E ( Y c ) } \Psi_{c}\left(Y_{c}\right)=\exp \left\{-E\left(Y_{c}\right)\right\} Ψc(Yc)=exp{−E(Yc)}
3. 条件随机场CRF
条件随机场是给定随机变量 X 下,随机变量Y的马尔科夫随机场。
P ( Y v ∣ X , Y n , w ≠ v ) = P ( Y v ∣ X , Y w , w ∼ v ) P\left(Y_{v} | X, Y_{n}, w \neq v\right)=P\left(Y_{v} | X, Y_{w}, w \sim v\right) P(Yv∣X,Yn,w=v)=P(Yv∣X,Yw,w∼v)
其中, w ∼ v w \sim v w∼v代表与结点 v v v有边连接的所有结点 w w w; w ≠ v w \neq v w=v代表结点 v v v以外的所有结点。
条件随机场的简单形式:
f k ( y i − 1 , y i , x , i ) = { t k ( y i − 1 , y i , x , i ) , k = 1 , 2 , ⋯ , K 1 s i ( y i , x , i ) , k = K 1 + l ; l = 1 , 2 , ⋯ , K 2 f_{k}\left(y_{i-1}, y_{i}, x, i\right)=\left\{\begin{array}{ll} t_{k}\left(y_{i-1}, y_{i}, x, i\right), & k=1,2, \cdots, K_{1} \\ s_{i}\left(y_{i}, x, i\right), & k=K_{1}+l ; l=1,2, \cdots, K_{2} \end{array}\right. fk(yi−1,yi,x,i)={tk(yi−1,yi,x,i),si(yi,x,i),k=1,2,⋯,K1k=K1+l;l=1,2,⋯,K2
f k ( y , x ) = ∑ i = 1 n f k ( y i − 1 , y i , x , i ) , k = 1 , 2 , ⋯ , K f_{k}(y, x)=\sum_{i=1}^{n} f_{k}\left(y_{i-1}, y_{i}, x, i\right), \quad k=1,2, \cdots, K fk(y,x)=i=1∑nfk(yi−1,yi,x,i),k=1,2,⋯,K
P ( y ∣ x ) = 1 Z ( x ) exp ∑ k = 1 K w k f k ( y , x ) Z ( x ) = ∑ y exp ∑ k = 1 K w k f k ( y , x ) \begin{aligned} P(y | x) &=\frac{1}{Z(x)} \exp \sum_{k=1}^{K} w_{k} f_{k}(y, x) \\ Z(x) &=\sum_{y} \exp \sum_{k=1}^{K} w_{k} f_{k}(y, x) \end{aligned} P(y∣x)Z(x)=Z(x)1expk=1∑Kwkfk(y,x)=y∑expk=1∑Kwkfk(y,x)
t k t_k tk代表转移特征, s l s_l sl代表状态特征, f k ( y , x ) f_k(y,x) fk(y,x)代表在该点的全局特征, w k w_k wk代表特征 f k ( y , x ) f_k(y,x) fk(y,x)的权值, Z ( x ) Z(x) Z(x)是归一化因子。
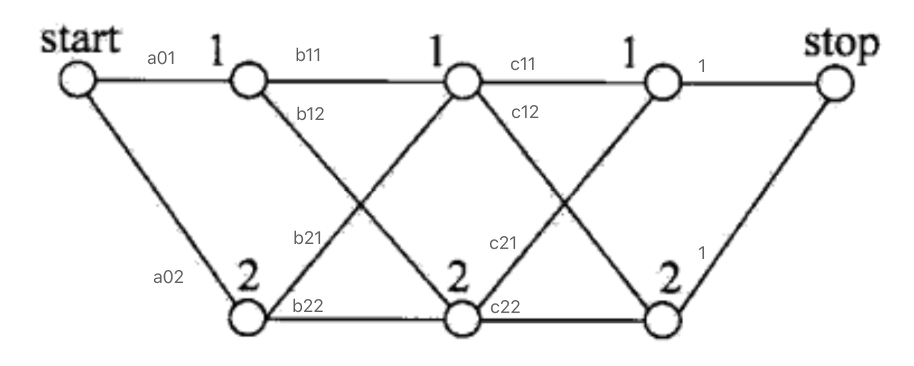
条件随机场的矩阵形式:
M i ( x ) = [ M i ( y i − 1 , y i ∣ x ) ] M i ( y i − 1 , y i ∣ x ) = exp ( W i ( y i − 1 , y i ∣ x ) ) W i ( y i − 1 , y i ∣ x ) = ∑ k = 1 K w k f k ( y i − 1 , y i , x , i ) \begin{array}{c} M_{i}(x)=\left[M_{i}\left(y_{i-1}, y_{i} | x\right)\right] \\ M_{i}\left(y_{i-1}, y_{i} | x\right)=\exp \left(W_{i}\left(y_{i-1}, y_{i} | x\right)\right) \\ W_{i}\left(y_{i-1}, y_{i} | x\right)=\sum\limits_{k=1}^{K} w_{k} f_{k}\left(y_{i-1}, y_{i}, x, i\right) \end{array} Mi(x)=[Mi(yi−1,yi∣x)]Mi(yi−1,yi∣x)=exp(Wi(yi−1,yi∣x))Wi(yi−1,yi∣x)=k=1∑Kwkfk(yi−1,yi,x,i)
条件概率:
P w ( y ∣ x ) = 1 Z w ( x ) ∏ i = 1 n + 1 M i ( y i − 1 , y i ∣ x ) P_{w}(y | x)=\frac{1}{Z_{w}(x)} \prod_{i=1}^{n+1} M_{i}\left(y_{i-1}, y_{i} | x\right) Pw(y∣x)=Zw(x)1i=1∏n+1Mi(yi−1,yi∣x)
3.1 概率计算问题
前向-后向算法;
1、概率计算:
α i T ( y i ∣ x ) = α i − 1 T ( y i − 1 ∣ x ) [ M i ( y i − 1 , y i ∣ x ) ] , i = 1 , 2 , ⋯ , n + 1 \alpha_{i}^{T}\left(y_{i} | x\right)=\alpha_{i-1}^{T}\left(y_{i-1} | x\right)\left[M_{i}\left(y_{i-1}, y_{i} | x\right)\right], i=1,2, \cdots, n+1 αiT(yi∣x)=αi−1T(yi−1∣x)[Mi(yi−1,yi∣x)],i=1,2,⋯,n+1
β i ( y i ∣ x ) = [ M i ( y i , y i + 1 ∣ x ) ] β i + 1 ( y i + 1 ∣ x ) \beta_{i}\left(y_{i} | x\right)=\left[M_{i}\left(y_{i}, y_{i+1} | x\right)\right] \beta_{i+1}\left(y_{i+1} | x\right) βi(yi∣x)=[Mi(yi,yi+1∣x)]βi+1(yi+1∣x)
即,
α i T ( x ) = α i − 1 T ( x ) M i ( x ) \alpha_{i}^{\mathrm{T}}(x)=\alpha_{i-1}^{\mathrm{T}}(x) M_{i}(x) αiT(x)=αi−1T(x)Mi(x)
β i ( x ) = M i + 1 ( x ) β i + 1 ( x ) \beta_{i}(x)=M_{i+1}(x) \beta_{i+1}(x) βi(x)=Mi+1(x)βi+1(x)
因此,条件概率:
P ( Y i = y i ∣ x ) = α i ⊤ ( y i ∣ x ) β i ( y i ∣ x ) Z ( x ) \begin{array}{c} P\left(Y_{i}=y_{i} | x\right)=\frac{\alpha_{i}^{\top}\left(y_{i} | x\right) \beta_{i}\left(y_{i} | x\right)}{Z(x)} \end{array} P(Yi=yi∣x)=Z(x)αi⊤(yi∣x)βi(yi∣x)
P ( Y i − 1 = y i − 1 , Y i = y i ∣ x ) = α i − 1 T ( y i − 1 ∣ x ) M i ( y i − 1 , y i ∣ x ) β i ( y i ∣ x ) Z ( x ) \begin{array}{c} P\left(Y_{i-1}=y_{i-1}, Y_{i}=y_{i} | x\right)=\frac{\alpha_{i-1}^{\mathrm{T}}\left(y_{i-1} | x\right) M_{i}\left(y_{i-1}, y_{i} | x\right) \beta_{i}\left(y_{i} | x\right)}{Z(x)} \end{array} P(Yi−1=yi−1,Yi=yi∣x)=Z(x)αi−1T(yi−1∣x)Mi(yi−1,yi∣x)βi(yi∣x)
3.2 条件随机场的学习算法
改进的迭代尺度法
拟牛顿法
3.3 条件随机场的预测算法
给定条件随机场P(Y|X),和输入序列x,求条件概率最大的输出序列y。
参考:
1、条件随机场_刘建平
2、IIS算法