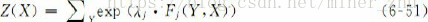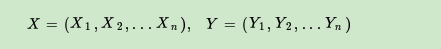转自：原文链接

条件随机场是一种判别模型，用于预测序列。他们使用来自先前标签的上下文信息，从而增加了模型做出良好预测所需的信息量。在这篇文章中，我将讨论一些将介绍 CRF 的主题。我会过去：

1. 什么是判别分类器（以及它们与生成分类器的比较）
2. 条件随机场的数学概述
3. CRF 与隐马尔可夫模型有何不同
4. CRF的应用

什么是判别分类器

机器学习模型有两个常见的分类，生成式和判别式。条件随机场是一种判别分类器，因此，它们对不同类之间的决策边界进行建模. 另一方面，生成模型对数据的生成方式进行建模，在学习之后，可用于进行分类任务。举个简单的例子，朴素贝叶斯是一种非常简单且流行的概率分类器，是一种生成算法，而逻辑回归是一种基于最大似然估计的分类器，是一种判别模型。让我们看看如何使用这些模型来计算标签预测：
朴素贝叶斯分类器基于贝叶斯公式：
$$p(y|x)=\frac{p(y)p(x|y)}{p(x)}$$
换成分类任务的表达式：
$$p(类别|特征)=\frac{p(特征|类别)p(类别)}{p(特征)}$$
通常特征$X$会包含很多元素$x_i$，类别$Y$也会包含很多类别$y_k$，所以
$$p(特征|类别)\to p(X|Y=y_k)$$
然后我们假设所有特征之间都是相互独立的，因此公式可以转换为：
$$\begin{gathered} p(X|Y=y_k)=\prod _i^{n}p(X=x_i|Y=y_k) \\ p(X)=p(x_1{x}_2\dots x_n) \end{gathered}$$
比如，我们想求 $p(皮薄,红,脆,水分多|苹果甜)$，则可以通过$p(皮薄|苹果甜)\ast p(红|苹果甜)\ast p(脆|苹果甜)\ast p(水分多|苹果甜)$得到。
带入到 $p(类别|特征)$可以得到：
$$p(Y=y_k|X)=\frac{p(Y=y_k){\prod }_i^{n}p(X=x_i|Y=y_k)}{p(x_1{x}_2\dots x_n)}$$
由于分母是常数，所以可以直接省略，因为朴素贝叶斯分类器的目的是为了找到使$p(Y=y_k|X)$最大的$y_k$。
$$p(y_k|X)\approx p(y_k)\prod _i^{n}p(x_i|y_k)$$
所以朴素贝叶斯分类器的公式如下：
$${\hat{y}}_k=argma{x}_{y_k}p(y_k)\prod _i^{n}p(x_i|y_k)$$

逻辑回归分类器是基于Logistic函数的，已知如下：
$$f(x)=\frac{1}{1+e^{-x}}=\frac{e^x}{1+e^x}$$
上述也是逻辑分布在$\mu =0,\gamma =1$的分布函数。回想一下朴素贝叶斯是通过贝叶斯公式从$p(X|y_k)$推出的$p(y_k|X)$，然而我们可以利用逻辑回归直接建模$p(y_k|X)$，同时也避免了线性回归的输出不在0-1之间（通过对线性输出进行对数odds）。
为了学习逻辑回归中两个类之间的决策边界，分类器学习与每个数据点相关的权重（θ值），写法如下：
$$\begin{gathered} 二元分类时，p(y_k|X;\theta )=\frac{1}{1+exp(-({\theta }_0+{\sum }_{f=1}^F{\theta }_f{x}_f))}=\frac{1}{1+exp({\theta }^{T}X)} \\ 多元分类时，使用softmax：p(y_k|X;\theta )=\frac{exp({\theta }_c^{T}X)}{{\sum }_{f}exp({\theta }_f^{T}X)} \end{gathered}$$
此时我们最后得到的分类$y_k$也是通过寻找最大概率得到的。
$$\hat{y}=argma{x}_{y_k}p(y_k|X)$$
如果把 $p(y_k|X)$又通过贝叶斯转换得到$p(X|y_k)p(y_k)$，就又得到了先前的朴素贝叶斯生成分类器。然而$p(X|y_k)p(y_k)$又等于$p(X|y_k)$，即$X,y_k$的联合分布。这一观察结果支持了生成分类器的早期定义。通过对类之间的联合概率分布进行建模，在给定标签 Y 和联合概率分布的情况下，生成模型可用于获取和“生成”输入点 X。类似地，判别模型通过学习条件概率分布，学习了分隔数据点的决策边界。因此，给定一个输入点，它可以使用条件概率分布来计算它的类别。

这些定义如何应用于条件随机场（Conditional Random Field, CRF）？条件随机场是一种判别模型，其基本原理是将逻辑回归应用于序列输入。如果熟悉隐马尔可夫模型（HMM），就会发现它们与 CRF 有一些相似之处，其中之一是它们也用于序列输入。HMM 使用状态转移矩阵和输入向量来学习发射（观测）矩阵，并且在概念上类似于朴素贝叶斯。HMM 是一种生成模型。

条件随机场的数学概述

讨论了上述定义后，我们现在将讨论条件随机场，以及如何使用它们来学习序列数据。
正如我们在上一节中所展示的，我们对条件分布建模如下：
$$\hat{y}=argma{x}_{y}p(y|x)$$
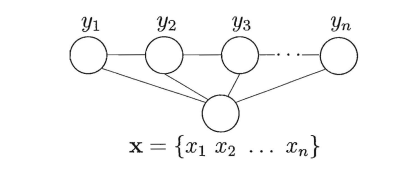
在 CRF 中，我们的输入数据是连续的，在对数据点进行预测时，我们必须考虑先前的上下文。为了建模这种行为，我们将使用特征函数，它有多个输入值，它们将是：

1. 输入向量集合 X
2. 我们正在预测的数据点的位置 i
3. X中数据点i-1的标签
4. X中数据点i的标签

我们将特征函数定义为：
$$f(X,i,l_{i-1},l_i)$$
特征函数的目的是表达数据点所代表的序列的某种特征。例如，如果我们使用 CRF 进行词性标注，那么：
如果 $l_{i-1}$ 是名词，$l_i$ 是动词，那我们认为$f(X,i,l_{i-1},l_i)=1$，也可以理解为这种顺序是合理的。否则为 0 。
类似地，如果 $l_{i-1}$ 是动词且$l_i$是副词，则$f(X,i,l_{i-1},l_i)=1$ 。否则为 0 。

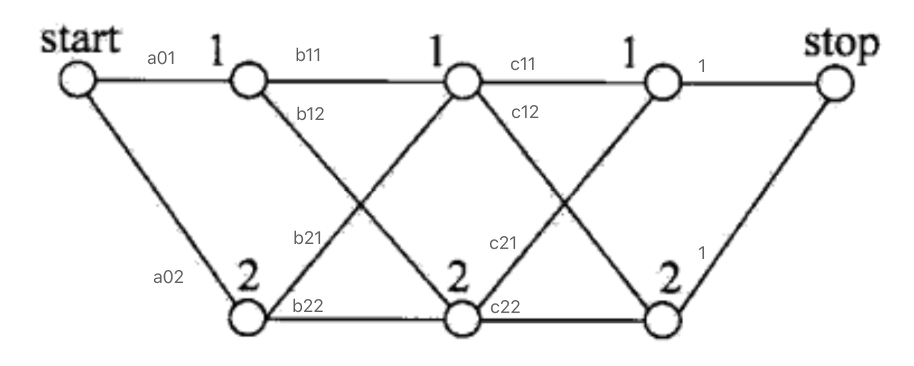
每个特征函数都基于前一个词和当前词的标签，并且是 0 或 1。为了构建条件字段，我们接下来为每个特征函数分配一组权重（λ值），公式如下（回想一下逻辑回归，记得CRF基本原理是将逻辑回归应用于序列输入）：
$$\begin{gathered} P(y|X,\lambda )=\frac{1}{Z(X)}exp\sum _{i=1}^n\sum _j{\lambda }_j{f}_i(X,i,y_{i-1},y_i) \\ 其中：Z(X)=\sum _{y^{\prime }\in y}\sum _{i=1}^n\sum _j{\lambda }_j{f}_i(X,i,y_{i-1}^{\prime },y_i^{\prime }) \end{gathered}$$
为了估计参数 (λ)，我们将使用最大似然估计。我们首先取分布的负对数(softmax通常和它搭配)，以使偏导数更易于计算：

为了在负对数函数上应用最大似然，我们将采用argmin（因为最小化负数将产生最大值）。为了找到最小值，我们可以对 lambda 进行偏导，并得到：

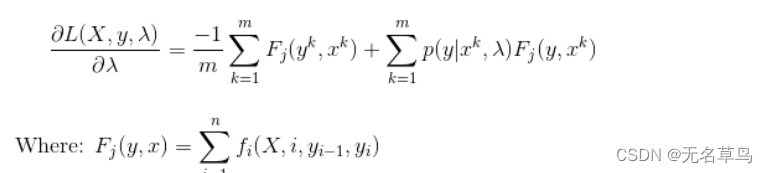
我们使用偏导作为梯度下降的一个步骤。梯度下降迭代地更新参数值，步长很小，直到值收敛。我们最终的 CRF 梯度下降更新方程是：

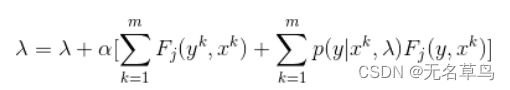
总而言之，我们使用条件随机场首先定义所需的特征函数，将权重初始化为随机值，然后迭代地应用梯度下降，直到参数值（在本例中为 lambda）收敛。我们可以看到 CRF 类似于 Logistic 回归，因为它们使用条件概率分布，但是我们通过将特征函数作为我们的顺序输入来扩展算法。

CRF 与隐马尔可夫模型有何不同

从前面的部分可以看出，条件随机场与隐马尔可夫模型有何不同。尽管两者都用于对顺序数据进行建模，但它们是不同的算法。

隐马尔可夫模型是生成的，并通过对联合概率分布建模来给出输出。另一方面，条件随机场具有判别性，并对条件概率分布进行建模。CRF 不依赖独立性假设（标签相互独立），并避免标签偏差。一种看待它的方法是，隐马尔可夫模型是条件随机场的一种非常特殊的情况，而是使用恒定的转移概率。HMMs 基于朴素贝叶斯，我们说它可以从逻辑回归中推导出来，而 CRF 就是从其中推导出来的。

CRF的应用

鉴于 CRF 能够对序列数据进行建模，CRF 通常用于自然语言处理，并且在该领域有很多应用。我们讨论的一个这样的应用是词性标注。句子的词性依赖于先前的单词，通过使用利用这一点的特征函数，我们可以使用 CRF 来学习如何区分句子中的哪些词对应于哪个 POS。另一个类似的应用是命名实体识别，或从句子中提取专有名词。条件随机场可用于预测多个变量相互依赖的任何序列。其他应用包括图像中的部分识别和基因预测。