二叉树的节点个数以及高度

---

---

前言

本文介绍二叉树的节点个数以及高度，每道题都附有源码+图解

---

NO.1 定义链式二叉树

代码如下（示例）：

typedef char BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType data;
}BTNode;

---

NO.2 创建二叉树

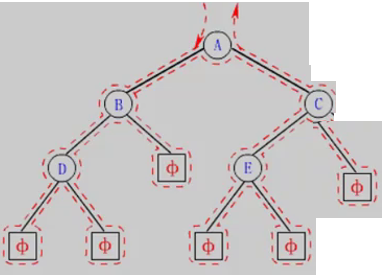
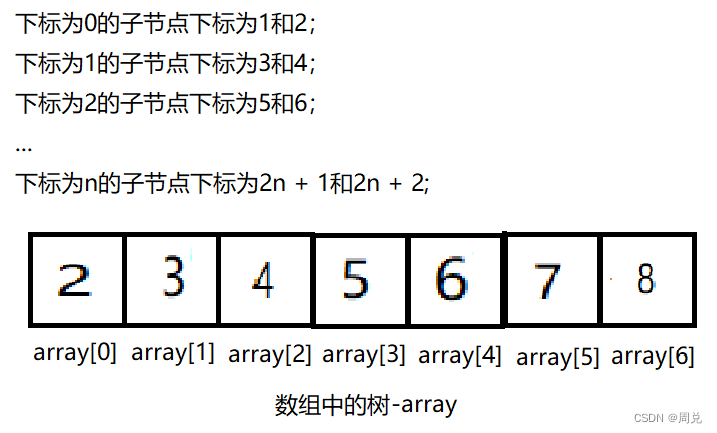
我们想要实现如图所示的链式二叉树，代码实现如下(把每一个节点都一一链接起来)

代码如下（示例）：

BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){printf("malloc fail\n");exit(-1);}node->data = x;node->left = node->right = NULL;return node;
}
BTNode* CreatBinaryTree()
{BTNode* nodeA = BuyNode('A');BTNode* nodeB = BuyNode('B');BTNode* nodeC = BuyNode('C');BTNode* nodeD = BuyNode('D');BTNode* nodeE = BuyNode('E');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeC->left = nodeE;return nodeA;
}

---

一、二叉树节点个数

我们刚创建完的二叉树中，节点个数有：5 个，下面是代码展示 + 递归图解！

1.代码展示

代码如下（示例）：

int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 :BinaryTreeSize(root->left)+ BinaryTreeSize(root->right)+ 1;
}

---

2.递归图解

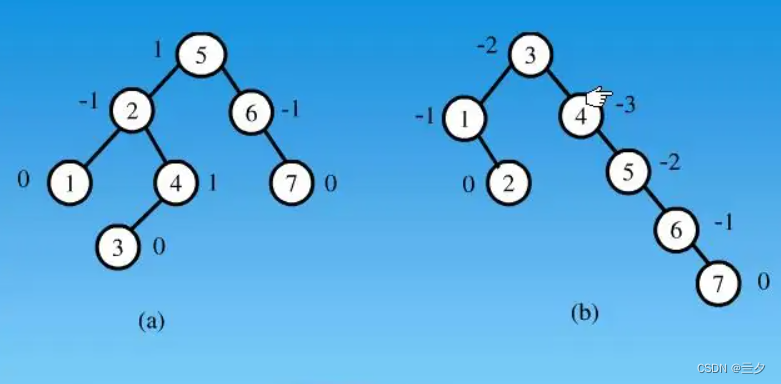
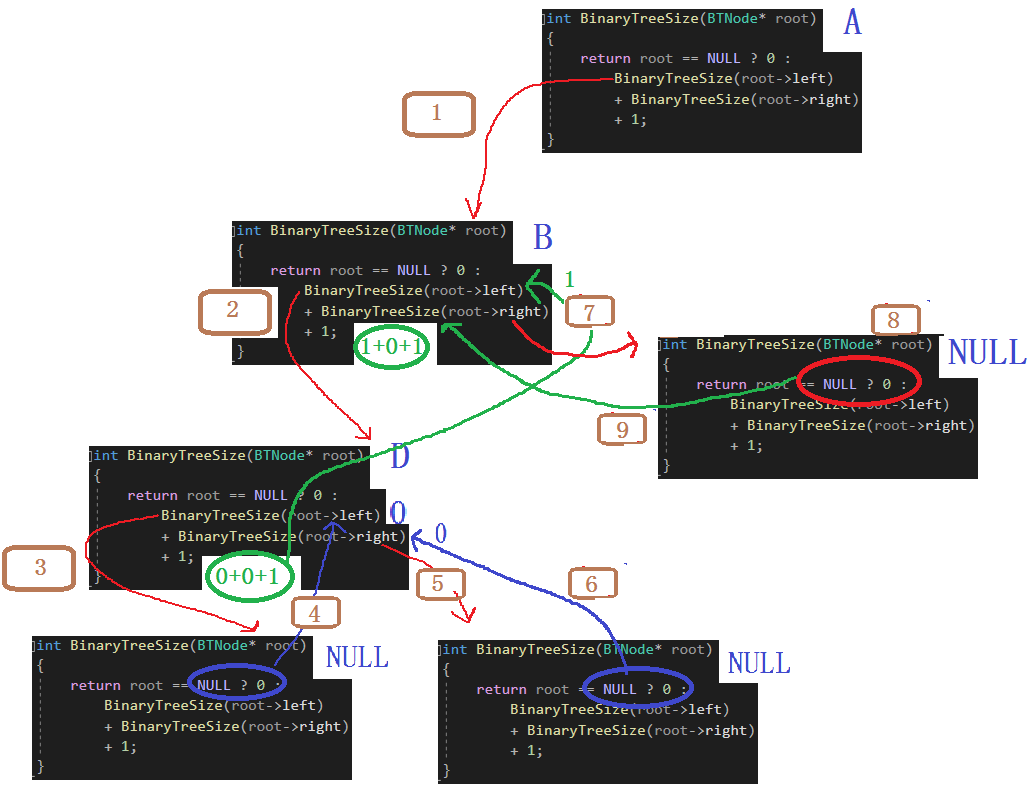
这里这画出了A左节点的递归展开图，右节点递归展开图和下面差不多，感兴趣的可以自行画图！

---

---

二、二叉树叶子节点个数

叶子节点：度为0的节点被称为叶节点，比如我们双肩的二叉树中的D和E两个节点！

1.代码展示

代码如下（示例）：

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

---

2.递归图解

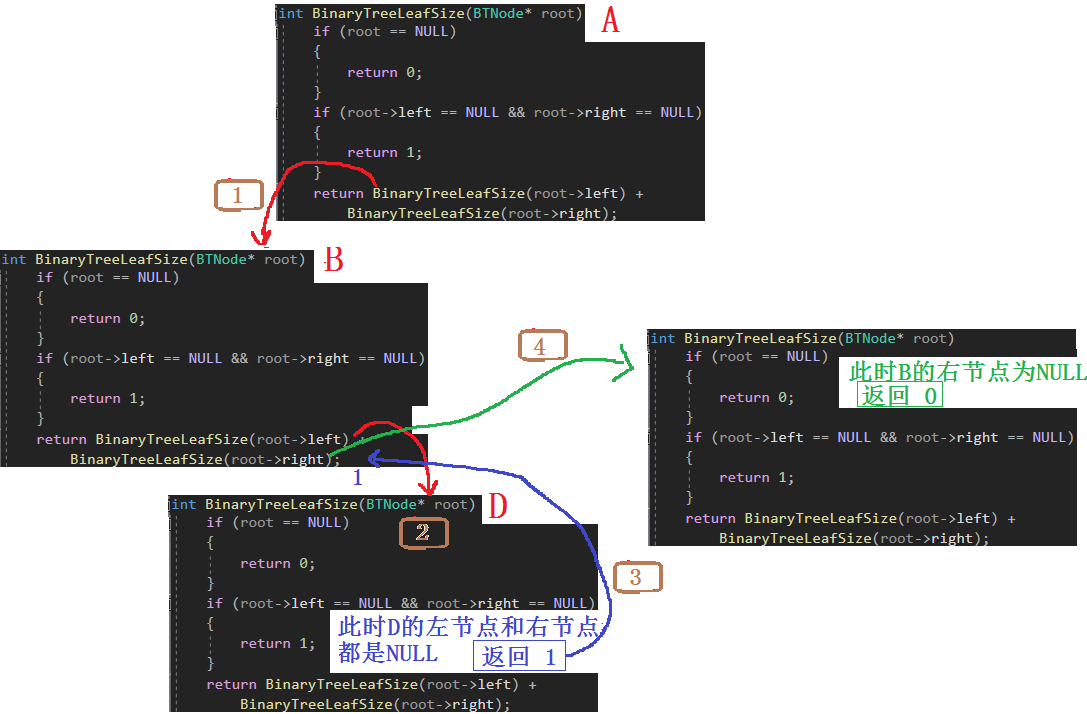
这里这画出了A左节点的递归展开图，右节点递归展开图和下面差不多，感兴趣的可以自行画图！

---

---

三、二叉树第k层节点个数

1.代码展示

代码如下（示例）：

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

---

2.递归图解

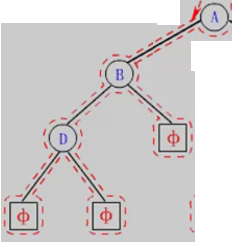
这里这画出了A左节点的递归展开图，右节点递归展开图和下面差不多，感兴趣的可以自行画图！

---

---

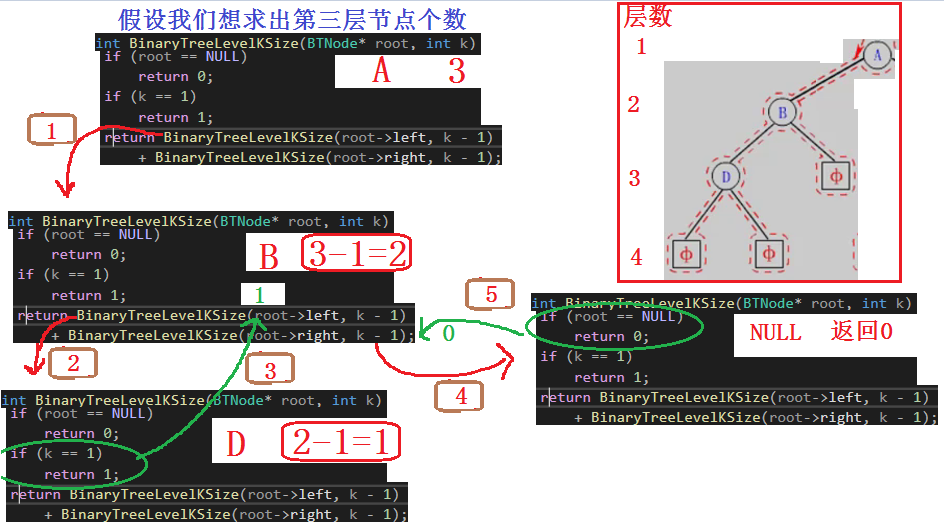
四、二叉树高度和深度

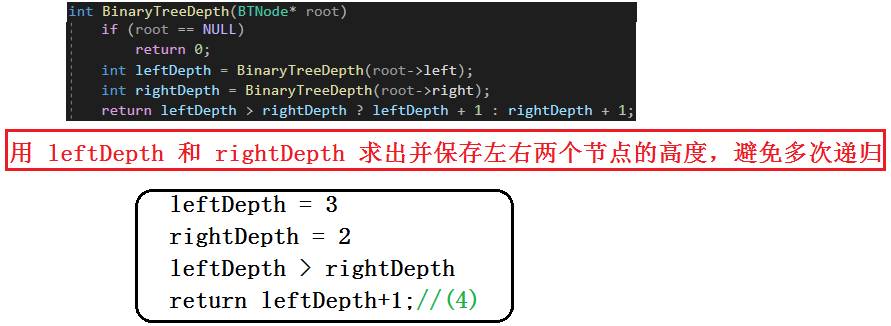
树的高度或深度：树中节点的最大层次。我们构建的二叉树的高度或深度为 4

1.代码展示

代码如下（示例）：

// 二叉树深度/高度
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}//return BinaryTreeDepth(root->left) > BinaryTreeDepth(root->right) /*? BinaryTreeDepth(root->left) + 1 : BinaryTreeDepth(root->right) + 1;*/int leftDepth = BinaryTreeDepth(root->left);int rightDepth = BinaryTreeDepth(root->right);return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

---

2.递归图解

这里这画出了A左节点的递归展开图，右节点递归展开图和下面差不多，感兴趣的可以自行画图！

---

---

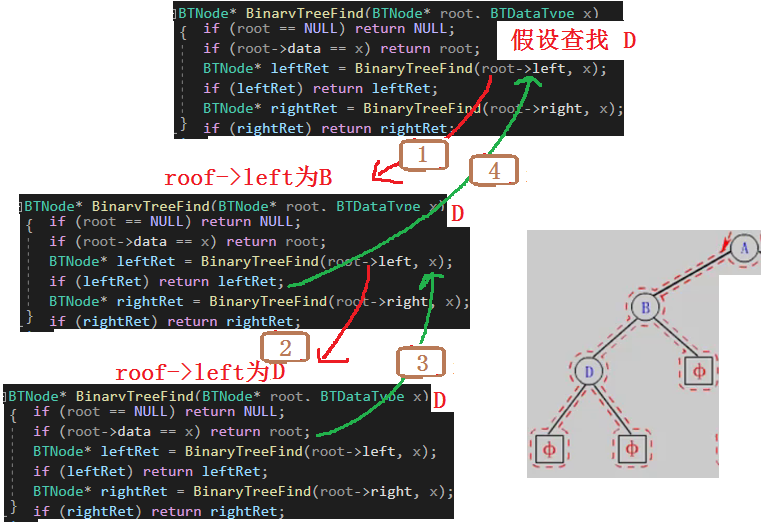
五、二叉树查找值为x的节点

1.代码展示

代码如下（示例）：

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* leftRet = BinaryTreeFind(root->left, x);if (leftRet)return leftRet;BTNode* rightRet = BinaryTreeFind(root->right, x);if (rightRet)return rightRet;return NULL;//return BinaryTreeFind(root->right, x);
}

---

2.递归图解

这里这画出了A左节点的递归展开图，右节点递归展开图和下面差不多，感兴趣的可以自行画图！

---

---

总结

以上就是今天要讲的内容，本文介绍二叉树的节点个数以及高度以及各自的递归展开图！
如果我的博客对你有所帮助记得三连支持一下，感谢大家的支持！