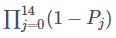机器学习：朴素贝叶斯的应用之垃圾邮件过滤

1.相关概念

1.条件概率：

条件概率是指某一事件A发生的可能性，表示P(A)。而条件概率指的是某一事件A已经发生了条件下，另一事件B发生的可能性，表示为P(B|A)。
怎么计算条件概率呢？设A,B是两个独立事件，且P(A)>0，称P(B|A)=P(AB)/P(A)为在事件A发生的条件下，事件B发生的条件概率。P(AB)表示事件A和B同时发生的概率。

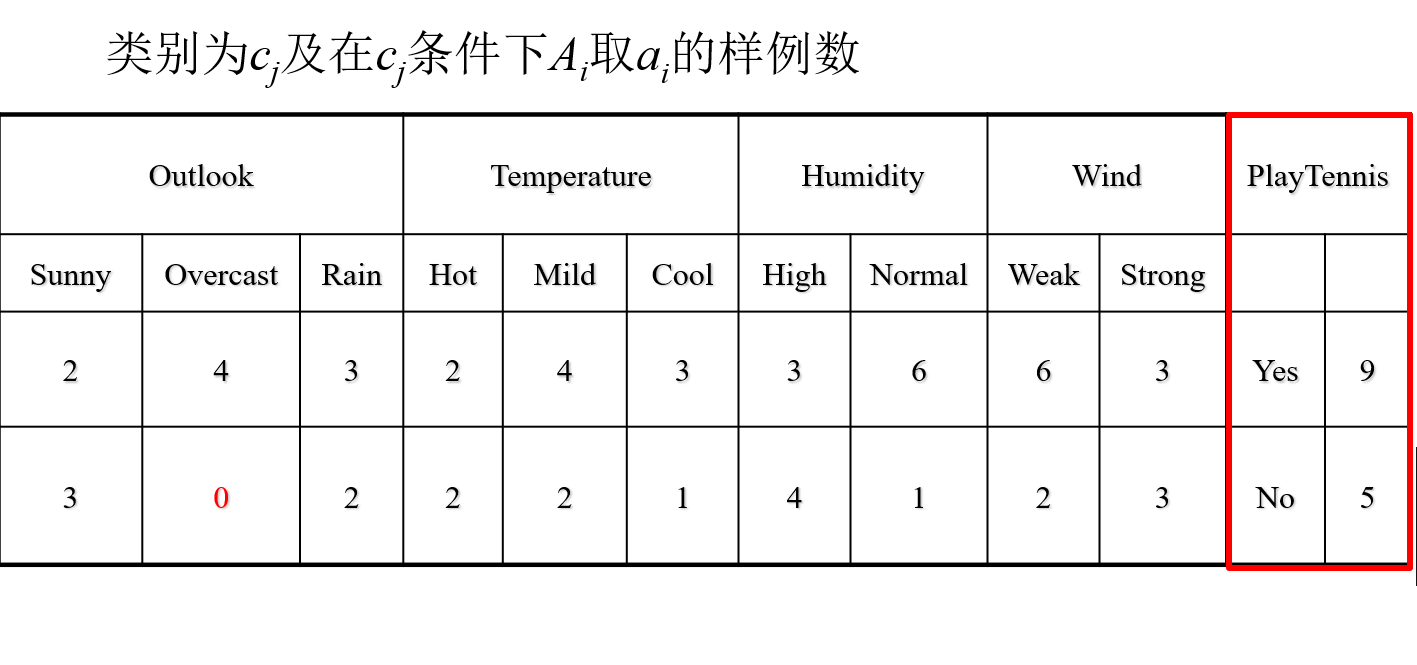
例如在上述数据中，要计算在已知Play Tennis成立时Outlook是Sunny的概率，这个时候其实就是在算条件概率。

假设事件A为Play Tennis成立，事件B为Outlook是Sunny，则根据表中数据可知P(AB)=2/14,P(A)=9/14 则P(B|A)=P(AB)/P(A)=2/9

2.贝叶斯公式：

当已知引发事件发生的各种原因的概率，想要算该事件发生的概率时，我们可以用全概率公式。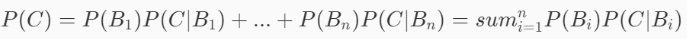

但是如若现在反过来，已知事件已经发生了，但是想要计算引发该事件的各种原因的概率时，我们就需要用到贝叶斯公式。

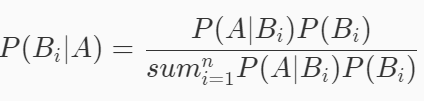
简单变换可得

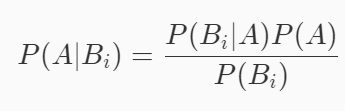
3.拉普拉斯平滑：

零概率：在计算事件的概率时，如果某个事件在观察样本库（训练集）中没有出现过，会导致该事件的概率结果是0。但是对于实际情况来说这是不合理的，不能因为一个事件没有观察到，就被认为该事件一定不可能发生（即该事件的概率为0）。这时就需要我们的拉普拉斯平滑(Laplacian smoothing) 。
拉普拉斯平滑指的是，假设N表示训练数据集总共有多少种类别，Ni表示训练数据集中第i总共有多少种取值。则训练过程种在算类别的概率时分子加1，分母加N，算条件概率时分子加1，分母加Ni。

2.朴素贝叶斯分类器

由贝叶斯公式可以推断朴素贝叶斯分类器是一个生成式模型（建立条件概率模型用于求解最大化后验模型）

以上述天气与是否打球数据为例，分析贝叶斯分类器的步骤

假设要求已知样例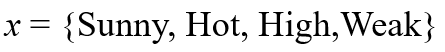的类别

将其归类在Play Tennis=Yes或Play Tennis=No上

1.根据已知数据计算先验概率以及条件概率

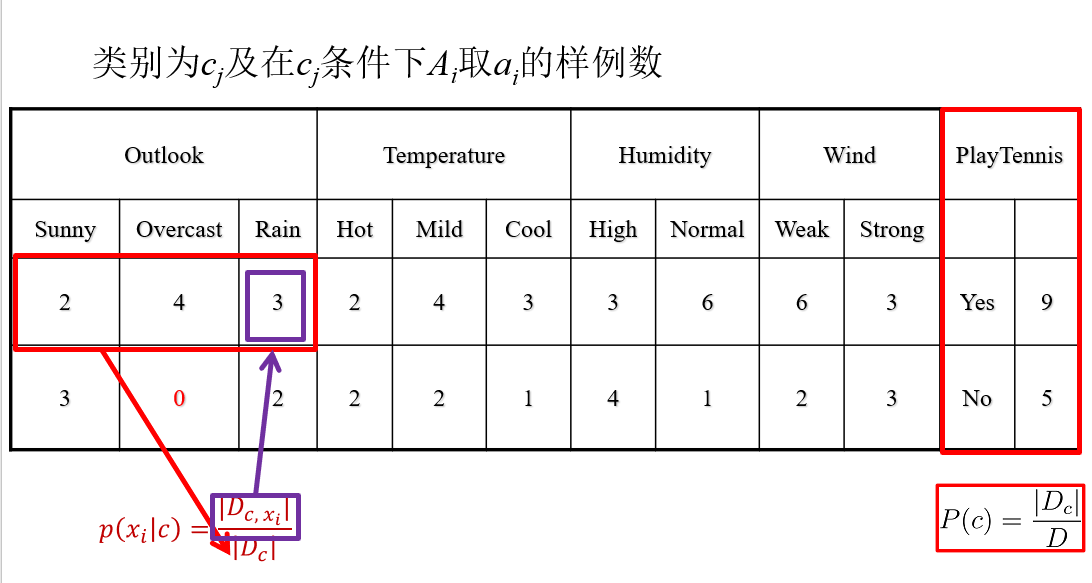
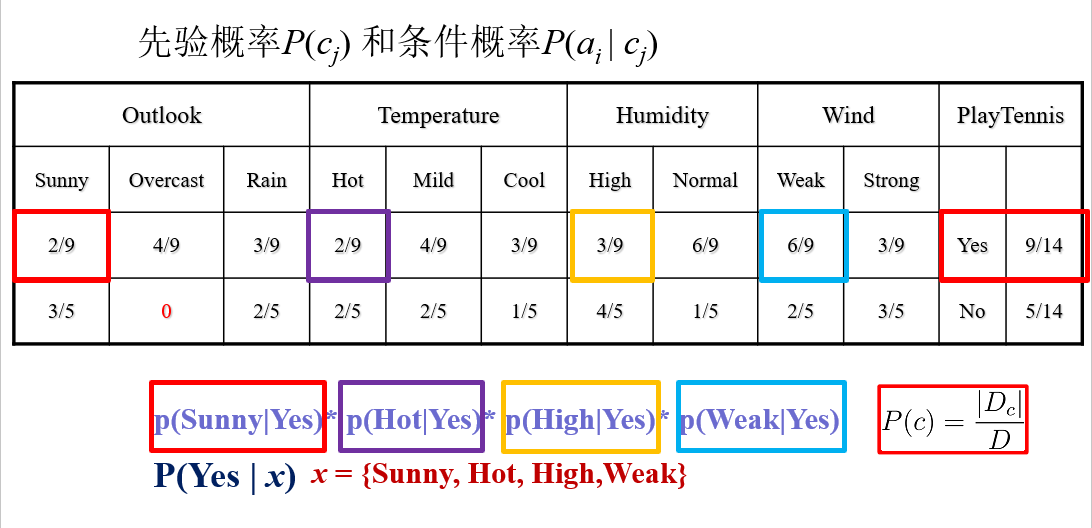
2.根据MAP分类准则与贝叶斯准则判定样例

注意点：

当遇到连续型数据时通过高斯分布计算

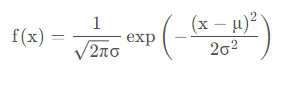
训练集中属性值未出现的情况下要进行“拉普拉斯修正”

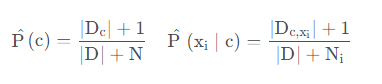
当属性数量多的情况下，导致累乘结果下溢。采用防溢出策略（累乘变累加）

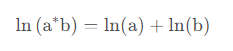
3.垃圾邮件的过滤（python实现）

1.数据集介绍

此数据集包含训练集train与测试集test ，训练集里包含24个以txt格式存储的普通邮件文本与24个以txt格式存储的垃圾邮件文本，测试集里包含普通邮件与垃圾邮件文本各一个，结构树如下

├─ Emails

│ ├─ test

│ │ ├─ normal.txt

│ │ └─ spam.txt

│ └─ Training

│ ├─ normal

│ │ ├─ 1.txt

│ │ ├─ 10.txt

│ │ ├─ 11.txt

│ │ ├─ …

│ └─ spam

│ ├─ 1.txt

│ ├─ 14.txt

│ ├─ 15.txt

│ ├─ …

2.数据预处理

邮件的具体内容基本类似：

需要对每一封邮件进行切割处理，得到包含所有词语的列表

具体的分割方法参考Python读取有空行的txt文件+将内容分割保存到列表中

def load_file(path):cab = []for i in range(1,25):data = open(path % i)for line in data.readlines():cab.append(line.strip().split(','))cab_f = []for i in range(len(cab)):for j in range(len(cab[i])):if cab[i][j] != '':cab_f.append(cab[i][j].strip())cab_final = []for i in cab_f:for j in i.split(' '):cab_final.append(j)return cab_final

3.构造朴素贝叶斯分类器

def bayes(sample):path1 = './Emails/Training/normal/%d.txt'path2 = './Emails/Training/spam/%d.txt'normal_data = load_file(path1)spam_data = load_file(path2)# 计算p(x|C1)=p1与p(x|C2)=p2p1 = 1.0p2 = 1.0for i in range(len(sample)):x = 0.0for j in normal_data:if sample[i] == j:x = x + 1.0p1 = p1 * ((x + 1.0) / (len(normal_data) + 2.0))  # 拉普拉斯平滑for i in range(len(sample)):x = 0.0for j in spam_data:if sample[i] == j:x = x + 1.0p2 = p2 * ((x + 1.0) / (len(spam_data) + 2.0))  # 拉普拉斯平滑pc1 = len(normal_data) / (len(normal_data) + len(spam_data))pc2 = 1 - pc1if p1 * pc1 > p2 * pc2:return 'normal'else:return 'spam'

4.测试并获得测试结果

def test(path):data = open(path)cab = []for line in data.readlines():cab.append(line.strip().split(','))cab_f = []for i in range(len(cab)):for j in range(len(cab[i])):if cab[i][j] != '':cab_f.append(cab[i][j].strip())cab_final = []for i in cab_f:for j in i.split(' '):cab_final.append(j)return bayes(cab_final)print(test('Emails/test/normal.txt'))
print(test('Emails/test/spam.txt'))

输出结果：

算法对于测试集中的邮件分类是正确的。

查看算法在训练集上多个邮件分类时的准确率

if __name__ == '__main__':sum1 = 0sum2 = 0# 再试试训练集for i in range(1, 25):if test('Emails/Training/normal/%d.txt' % i) == 'normal':sum1 = sum1 + 1for i in range(1, 25):if test('Emails/Training/spam/%d.txt' % i) == 'spam':sum2 = sum2 + 1print('normal分类正确率：', sum1 / 24)print('spam分类正确率：', sum2 / 24)

输出结果：

算法在训练集上的分类正确率很高，分类效果很好。

完整代码

import osdef load_file(path):cab = []for i in range(1,25):data = open(path % i)for line in data.readlines():cab.append(line.strip().split(','))cab_f = []for i in range(len(cab)):for j in range(len(cab[i])):if cab[i][j] != '':cab_f.append(cab[i][j].strip())cab_final = []for i in cab_f:for j in i.split(' '):cab_final.append(j)return cab_final# 朴素贝叶斯分类器
def bayes(sample):path1 = './Emails/Training/normal/%d.txt'path2 = './Emails/Training/spam/%d.txt'normal_data = load_file(path1)spam_data = load_file(path2)# 计算p(x|C1)=p1与p(x|C2)=p2p1 = 1.0p2 = 1.0for i in range(len(sample)):x = 0.0for j in normal_data:if sample[i] == j:x = x + 1.0p1 = p1 * ((x + 1.0) / (len(normal_data) + 2.0))  # 拉普拉斯平滑for i in range(len(sample)):x = 0.0for j in spam_data:if sample[i] == j:x = x + 1.0p2 = p2 * ((x + 1.0) / (len(spam_data) + 2.0))  # 拉普拉斯平滑pc1 = len(normal_data) / (len(normal_data) + len(spam_data))pc2 = 1 - pc1if p1 * pc1 > p2 * pc2:return 'normal'else:return 'spam'# 测试
def test(path):data = open(path)cab = []for line in data.readlines():cab.append(line.strip().split(','))cab_f = []for i in range(len(cab)):for j in range(len(cab[i])):if cab[i][j] != '':cab_f.append(cab[i][j].strip())cab_final = []for i in cab_f:for j in i.split(' '):cab_final.append(j)return bayes(cab_final)if __name__ == '__main__':# print(test('Emails/test/normal.txt'))# print(test('Emails/test/spam.txt'))sum1 = 0sum2 = 0# 再试试训练集for i in range(1, 25):if test('Emails/Training/normal/%d.txt' % i) == 'normal':sum1 = sum1 + 1for i in range(1, 25):if test('Emails/Training/spam/%d.txt' % i) == 'spam':sum2 = sum2 + 1print('normal分类正确率：', sum1 / 24)print('spam分类正确率：', sum2 / 24)