倾向值分析（协变量选择）

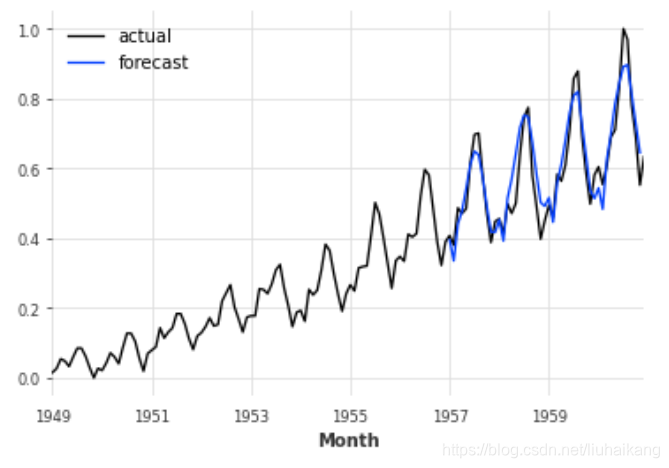
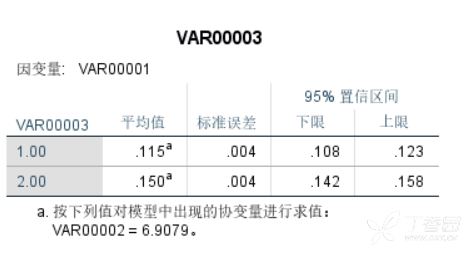
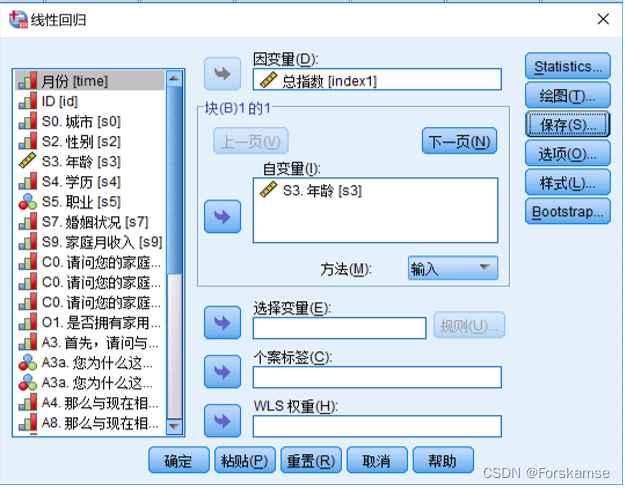
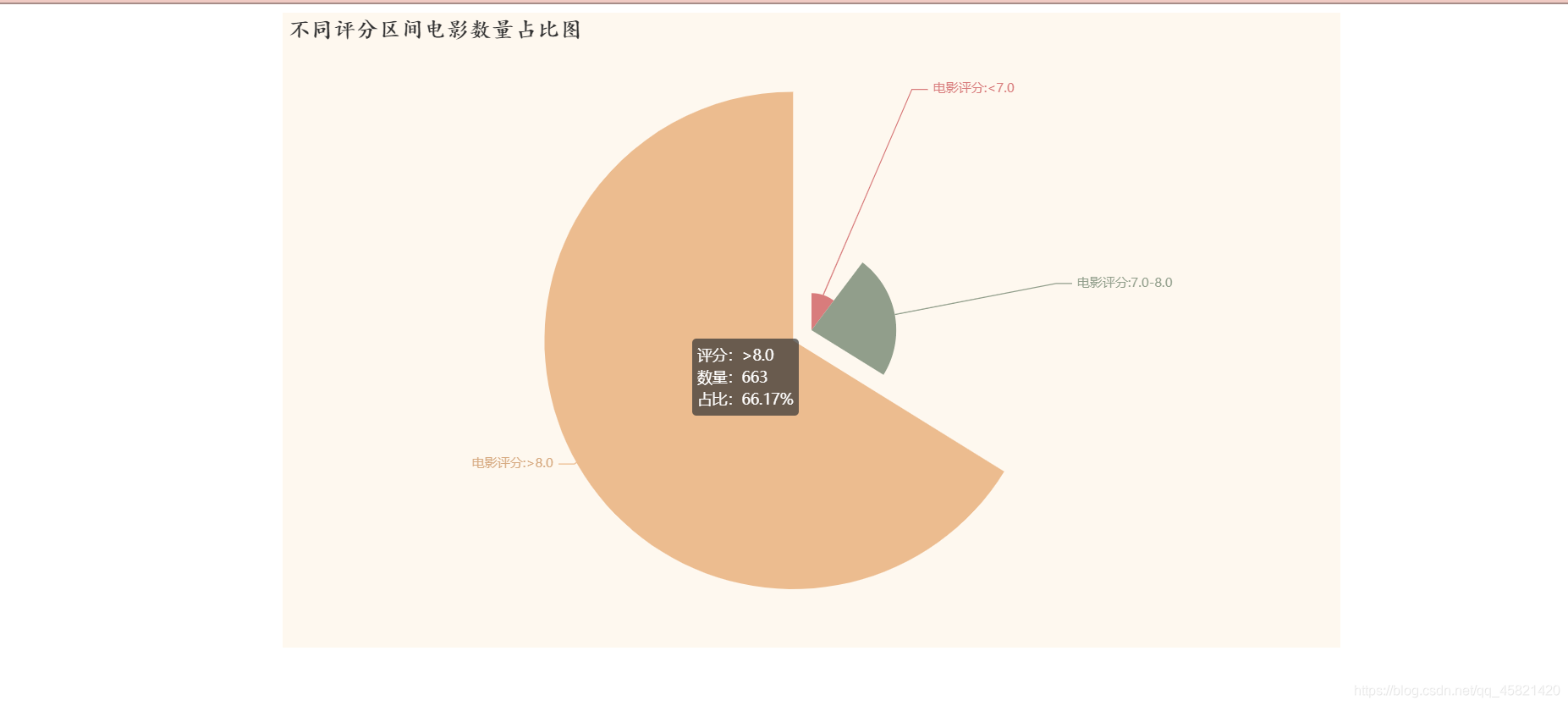
Hirano 和 Imbens 基于预设的临界t值来设定预测变量的方法

逻辑回归：逻辑回归虽然带有回归字样，但是逻辑回归属于分类算法。逻辑回归可以进行多分类操作，但由逻辑回归算法本身性质决定其更常用于二分类。
a.逻辑回归公式如下：

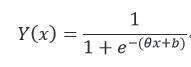
其中，Y为决策值，x为特征值，e为自然对数。Y(x)的图形如下：

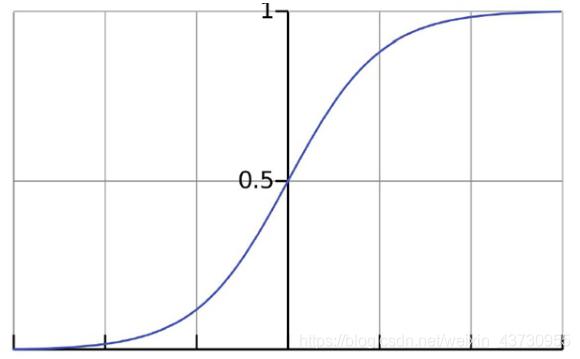
对于常见二分类，逻辑回归通过一个区间分布进行划分，即如果Y值大于等于0.5,则属于正样本，如果Y值小于0.5，则属于负样本，这样就可以得到逻辑回归模型，判别函数如下：

在模型参数w与b没有确定的情况下，模型是无法工作的，因此接下来就是在实际应用期间最重要的是模型参数w和b的估计。其代价函数如下：

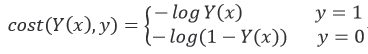
给定y值为1时，代价函数曲线横坐标为决策函数Y(x)的值越接近1，则代价越小,反之越大。当决策函数Y(x)的值为1时，代价为0。类似的，当给定y值为0时有同样的性质。
b.Logistic回归虽然名字叫”回归” ，但却是一种分类学习方法。使用场景大概有两个：第一用来预测，第二寻找因变量的影响因素。
c.odds: 称为几率、比值、比数，是指某事件发生的可能性(概率)与不发生的可能性（概率）之比。用p表示事件发生的概率，则：odds = p/(1-p)。
OR：比值比，为实验组的事件发生几率(odds1)/对照组的事件发生几率(odds2)。
d.最大似然法是要解决这样一个问题：给定一组数据和一个参数待定的模型，如何确定模型的参数，使得这个确定参数后的模型在所有模型中产生已知数据的概率最大。
e.可以通过逻辑回归系数衡量自变量对分类因变量的影响。详见链接中包含一个连续变量的模型部分
http://blog.sina.com.cn/s/blog_44befaf60102vznn.html
f.关于逻辑回归的代码分析见链接
https://baijiahao.baidu.com/s?id=1628902000717534995&wfr=spider&for=pc
利用python实现一元线性回归https://blog.csdn.net/LULEI1217/article/details/49385531
T检验
a.T检验是假设检验的一种，又叫student t检验（Student’s t test），主要用于样本含量较小（例如n<30），总体标准差σ未知的正态分布资料。
b. T检验用于检验两个总体的均值差异是否显著。
c. T检验使用了样本方差估计总体方差。
两样本均数比较
两独立样本均数 T 检验用于比较两样本所分别代表的总体均数是否有统计学差异。理论上，即使样本量很小时，也可以进行 T 检验, 如样本量为 10。一些学者声称甚至更小的样本也行，只要每组中变量呈正态分布，两组方差不是明显不同。正态分布假设可以通过观察数据的分布（如直方图、箱体图、Q-Q图）或进行正态性检验来测量。方差齐性的假设可进行 F 检验，或进行更有效的 Levene’s 检验。如果不满足这些条件，使用非参数检验代替 T 检验进行两组间均值的比较。如果呈正态分布，但方差不齐，可采用 Welch’s t test 方法。
配对 t 检验的基本原理是计算每对的差值（X= X1-X2），然后采用单样本 T 检验方法，检验差值是否等于 0，以此推断配对样本间是否有显著差异。
两独立样本t检验：
第一步：零假设：H0 μ1=μ2
第二步：判断两总体方差是否相等。（F检验，如果F对应的p值小于0.05，则方差不等；若果F对应的p值大于0.05，则方差相等）
第三步：构造t统计量并计算t和p值
第四步：判断，若p<0.05,则两总体均值存在显著差异，反之则不存在。
两独立样本及两配对样本t检验：http://blog.sina.com.cn/s/blog_5d188bc40101p6xu.html
T检验的原理：在原假设成立的基础上，求出”取得样本均值或者更极端的均值”的概率，如果概率很大，就倾向于认为原假设H0是正确的，如果概率很小，就倾向于认为原假设H0是错误的，从而接受备择假设H1。
https://blog.csdn.net/m0_37777649/article/details/74937242
http://blog.sina.com.cn/s/blog_5d188bc40101p6xu.html
T检验、F检验及统计学意义
https://wenku.baidu.com/view/0ff60f5def06eff9aef8941ea76e58fafab045cb.html
由于样本的随机性，回归系数估计出的结果肯定和真实值β之间有误差, 而且这一误差的分布会服从一定的规律，回归系数的标准差就是用来描述这个误差的波动的。
t检验是对单一系数的假设检验，F检验是对多个系数的joint hypothesis test，所以可以说t检验是F检验的一种特例。t检验也不一定要在多元线性回归中啦,一元线性也可以。
线性回归系数方差的计算：
回归：通过显著性检验判断因变量对结果变量的影响（假设真实回归系数为0后得到通过样本计算所得到回归系数出现的概率很小，则拒绝原假设）
多元线性回归中的 T 检验怎样理解？其 p 值为什么划定在 0.05？
https://www.zhihu.com/question/30753175
T值检验回归系数是否等于某一特定值，在回归方程中这一特定值为0，因此T值=回归系数/回归系数的标准误差，因此T值的正负应该与回归系数的正负一致，回归系数的标准误差越大，T值越小，回归系数的估计值越不可靠，越接近于0。另外，回归系数的绝对值越大，T值的绝对值越大。
回归分析中15个统计量解释 http://www.sohu.com/a/278722118_556897
我们在估计的时候都是用样本估计的，抽取一个样本就可以得到一个估计系数，再抽取一个还可以得到一个不同的估计系数，所以估计系数本身就是随机变量。而这种随机变量（由于是通过抽样获得的）的标准差就叫做标准误差。

逐步回归法

一个好的回归模型并不是考虑的自变量越多越好。在建立回归模型时选择自变量的指导思想是“少而精”。
无偏估计：估计量的数学期望等于被估计参数的真实值，则称此此估计量为被估计参数的无偏估计，即具有无偏性，是一种用于评价估计量优良性的准则。无偏估计的意义是：在多次重复下，它们的平均数接近所估计的参数真值。
关于自变量选取的几个准则（abc适用于自变量个数较少的情况,d适用于自变量个数较多的情况）：
a. 自由度调整复相关系数达到最大
b. 赤池信息量AIC达到最小
c. C_p统计量达到最小
d. 前进法，后退法，逐步回归法
Pearson相关系数的适用范围：
a. 两个变量之间是线性关系，都是连续数据；
b. 两个变量的总体是正态分布，或接近正态分布；
c. 两个变量的观测值是成对的，每对观测值之间相互独立。
为什么进行显著性检验：
要从样本系数判断总体中是否也有这样的关系，则需要对相关系数进行统计检验后才能得出结论。
T检验与F检验的由来：一般为确定从样本统计结果推至总体时所犯错的几率，我们会利用统计学家开发的统计方法（F检验，T检验）进行统计检定。F值和T值就是对应的统计检定值，与他们相对应的分布就是F分布和T分布。统计显著性（sig）就是目前出现样本这结果的几率。
F检定的作用：均数差别的显著性检验，分离各有关因素并估计其对总变异的作用，分析因素之间的交互作用。
逐步回归法：逐步回归的基本思想是“有进有出”。具体做法是将变量一个个引入，当每引入一个变量后，对已选入的变量进行逐个检验，当原引入的变量由于后面变量的引入而变得不显著时，样将其剔除。这个过程反复进行，直到既无显著的自变量选入回归方程，也无不显著的变量从回归方程中剔除为止。
自变量的选择与逐步回归分析
https://wenku.baidu.com/view/561ec3e4793e0912a21614791711cc7931b778e6.html

OLS线性回归法

正态分布与T分布的关系：t分布的自由度趋于无穷时，t分布就服从正态分布所以，正态分布可以看做t分布的一个特例。
假设检验
a. 基本思想是概率性质的反证法，即小概率事件原理：该原理认为小概率事件在一次实验中是不可能发生的。那么，在假定原假设是正确的条件下构造的一个检验统计量是小概率事件，如果小概率事件发生了，说明原假设是错误的，因为不该出现的小概率事件出现了，应该拒绝原假设。
b. 假设检验包含两种方法：
①置信区间检验法
②t检验（单个变量系数的显著性检验）或F检验（多个变量系数的联合性显著检验）

最小二乘线性（OLS）回归模型
http://blog.sina.com.cn/s/blog_17bf54ea20102x70y.html

使用 psestimate 这一命令来选择能最好拟合处理变量 (treat) 的协变量的一阶及二阶形式

https://blog.csdn.net/arlionn/article/details/90108138

逻辑回归计算特征重要度

变量贡献率，反应各自变量对因变量影响程度的相对大小，计算步骤如下：

对所有自变量标准化；
对标准化后的自变量建逻辑回归模型，取各变量回归系数的绝对值；
计算各变量回归系数绝对值的占比即为特征贡献率。
注：虚拟变量，也叫哑变量，可用来表示分类变量、非数量因素可能产生的影响。在计量经济学模型，需要经常考虑属性因素的影响。例如，职业、文化程度、季节等属性因素往往很难直接度量它们的大小。只能给出它们的“Yes—D=1”或”No—D=0”，或者它们的程度或等级。为了反映属性因素和提高模型的精度，必须将属性因素“量化”。通过构造0-1型的人工变量来量化属性因素。
Python实现逻辑回归：https://blog.csdn.net/t15600624671/article/details/77992969

随机森林输出特征重要度

用随机森林进行特征重要性评估的思想其实很简单，通俗来讲就是看每个特征在随机森林中的每颗树上做了多大的贡献，取平均值，然后比较特征之间的贡献大小。
常见的计算方法有两种，一种是平均不纯度的减少（mean decrease impurity），常用gini /entropy /information gain测量，现在sklearn中用的就是这种方法；另一种是平均准确率的减少（mean decrease accuracy），常用袋外误差率去衡量。
平均准确率的减少（mean decrease accuracy）即对每个特征加躁，看对结果的准确率的影响。影响小说明这个特征不重要，反之重要。
风险：随机森林的变量重要性衡量的并不完全是变量对目标变量预测的贡献能力，而是在这个模型中对目标变量预测的贡献能力，所以单纯用来评价变量的重要性值得探究。例如：我们有A和B两个变量，且A和B之间有较强的相关性，如果A对模型贡献度较大，由于B很像A，所以B也应该对模型贡献较大，但实际上若在随机森林中输出A的特征重要度得分高，B得分往往会很低。
特征重要度整理 - 随机森林、逻辑回归：
https://blog.csdn.net/weixin_39795364/article/details/82956118