基于 Python（gma） 的 克里金（Kriging）法插值的主要过程

article/2025/5/22 4:40:42

  由于克里金插值的复杂性，本文不再对其原理进行介绍。详情可自行百度。

  • 本算法基于 Python 的开源克里金插值包 pykrige。
  • 但本算法已对其进行改造，以使其符合 gma 的整体逻辑。
  • 本算法已不包含任何 pykrige 的原始代码。

原始代码构建

from gma.algorithm.spmis.interpolate import *class Kriging(IPolate):'''克里金法插值'''# 继承 gma 的标准插值类 IPolate。本处不再做详细说明。def __init__(self, Points, Values, Boundary = None, Resolution = None, InProjection = 'WGS84', VariogramModel = 'Linear',VariogramParameters = None,**kwargs):IPolate.__init__(self, Points, Values, Boundary, Resolution, InProjection)self.eps = eps# 初始化半变异函数及参数self.VariogramModel, self.VParametersList = GetVariogramParameters(VariogramModel, VariogramParameters)self.VariogramFUN = getattr(variogram, self.VariogramModel)if self.VParametersList is None:self.VParametersList = self._INITVariogramModel(**kwargs)# 调整输入数据if self.GType == 'PROJCS':self.Center = (self.Points.min(axis = 0) + self.Points.max(axis = 0)) * 0.5self.AnisotropyScaling = AnisotropyScalingself.AnisotropyAngle = AnisotropyAngleself.DistanceMethod = cdistelse:# 方便后期优化self.Center = np.array([0,0])self.AnisotropyScaling = 1.0self.AnisotropyAngle = 0.0self.DistanceMethod = GreatCircleDistanceself.AdjustPoints = AdjustAnisotropy(self.Points, self.Center, [self.AnisotropyScaling], [self.AnisotropyAngle])self.XYs = AdjustAnisotropy(self.XYs, self.Center,[self.AnisotropyScaling], [self.AnisotropyAngle])def _INITVariogramModel(self, **kwargs):'''初始化参数'''if 'NLags' in kwargs:NLags = kwargs['NLags']initialize.ValueType(NLags, 'pint')else:NLags = 6if 'Weight' in kwargs:Weight = ToNumericArray(kwargs['Weight']).flatten().astype(bool)[0]else:Weight = FalseLags, SEMI = INITVariogramModel(self.Points, self.Values, NLags, self.GType)# 为求解自动参数准备if self.VariogramModel == "Linear":X0 = [np.ptp(SEMI) / np.ptp(Lags), np.min(SEMI)]BNDS = ([0.0, 0.0], [np.inf, np.max(SEMI)])elif self.VariogramModel == "Power":X0 = [np.ptp(SEMI) / np.ptp(Lags), 1.1, np.min(SEMI)]BNDS = ([0.0, 0.001, 0.0], [np.inf, 1.999, np.max(SEMI)])else:X0 = [np.ptp(SEMI), 0.25 * np.max(Lags),  np.min(SEMI)]BNDS = ([0.0, 0.0, 0.0], [10.0 * np.max(SEMI), np.max(Lags), np.max(SEMI)])# 最小二乘法求解默认参数def _VariogramResiduals(Params, X, Y, Weight):if Weight:Weight = 1.0 / (1.0 + np.exp(-2.1972 / (0.1 * np.ptp(X)) * (0.7 * np.ptp(X) + np.min(X) - x))) + 1 else:Weight = 1return (self.VariogramFUN(X, *Params) - Y) * WeightRES = least_squares(_VariogramResiduals, X0, bounds = BNDS, loss = "soft_l1",args = (Lags, SEMI, Weight))return RES.xdef _GetKrigingMatrix(self):"""获取克里金矩阵"""LDs = self.DistanceMethod(self.AdjustPoints, self.AdjustPoints)A = -self.VariogramFUN(LDs, *self.VParametersList)A = np.pad(A, (0, 1), constant_values = 1)# 填充主对角线np.fill_diagonal(A, 0.0)return  Adef _UKExec(self, A, LDs, SearchRadius):"""泛克里金求解"""Args = LDs.argsort(axis = 1)[:,:SearchRadius]Values = self.Values[Args.T].T# A 的逆矩阵AInv = inv(A)B = -self.VariogramFUN(LDs, *self.VParametersList)B[np.abs(LDs) <= self.eps] = 0.0B = np.pad(B, ((0,0),(0,1)), constant_values = 1)X = np.dot(B, AInv)B = B[np.ogrid[:len(B)], Args.T].TX = X[np.ogrid[:len(X)], Args.T].TX = X / X.sum(axis = 1, keepdims = True)UKResults = np.sum(X * Values, axis = 1), np.sum((X * -B), axis = 1)return UKResultsdef _OKExec(self, A, LDs, SearchRadius):"""普通克里金求解"""Args = LDs.argsort(axis = 1)[:,:SearchRadius]LDs = LDs[np.ogrid[:len(LDs)], Args.T].TB = -self.VariogramFUN(LDs, *self.VParametersList)B[np.abs(LDs) <= self.eps] = 0.0B = np.pad(B, ((0,0),(0,1)), constant_values = 1)OKResults = np.zeros([2, len(LDs)])for i, b in enumerate(B):BSelector = Args[i] ASelector = np.append(BSelector, len(self.AdjustPoints))a = A[ASelector[:, None], ASelector]  x = solve(a, b)OKResults[:, i] = x[:SearchRadius].dot(self.Values[BSelector]), -x.dot(b)return OKResultsdef Execute(self, SearchRadius = 12, KMethod = 'Ordinary'):'''克里金插值'''initialize.ValueType(SearchRadius, 'pint')SearchRadius = np.min([SearchRadius, len(self.AdjustPoints)])A = self._GetKrigingMatrix()LDs = self.DistanceMethod(self.XYs, self.AdjustPoints)if KMethod not in ['Universal', 'Ordinary']:raise ValueError("Undefined Kriging method. Please select 'Universal' or 'Ordinary'!")elif KMethod == 'Universal':KResults = self._UKExec(A, LDs, SearchRadius)else:KResults = self._OKExec(A, LDs, SearchRadius)NT = namedtuple('Kriging', ['Data', 'SigmaSQ', 'Transform'])return NT(KResults[0].reshape(self.YLAT, self.XLON),KResults[1].reshape(self.YLAT, self.XLON), self.Transform)

插值应用

在 gma 1.0.13.15 之后的版本可以直接引用。

import gma
import pandas as pdData = pd.read_excel("Interpolate.xlsx")
Points = Data.loc[:, ['经度','纬度']].values
Values = Data.loc[:, ['值']].values# 普通克里金（球面函数模型）插值
KD = Kriging(Points, Values,Resolution = 0.05, VariogramModel = 'Spherical', VariogramParameters = None,InProjection = 'EPSG:4326').Execute(KMethod = 'Ordinary')# 泛克里金类似，这里不做示例gma.rasp.WriteRaster(r'.\gma_OKriging.tif',KD.Data,Projection = 'WGS84',Transform = KD.Transform, DataType = 'Float32')

结果对比

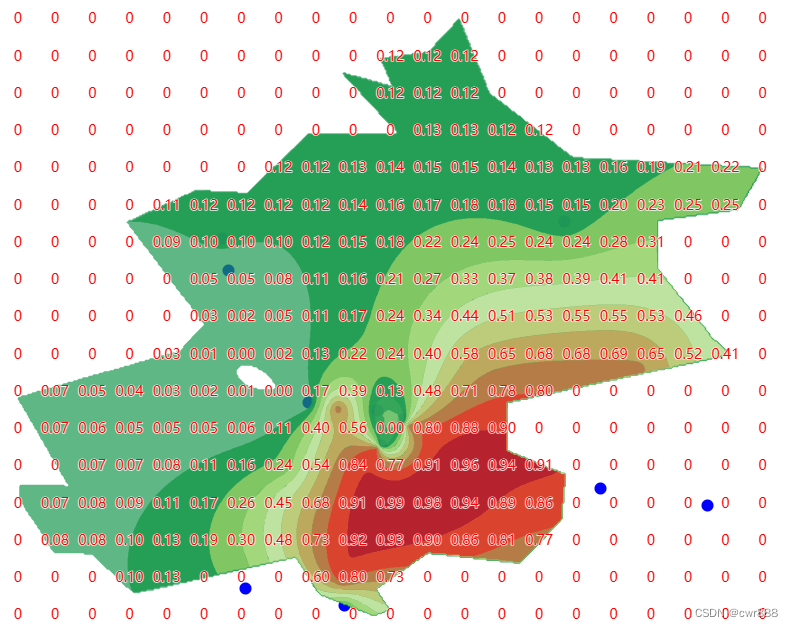
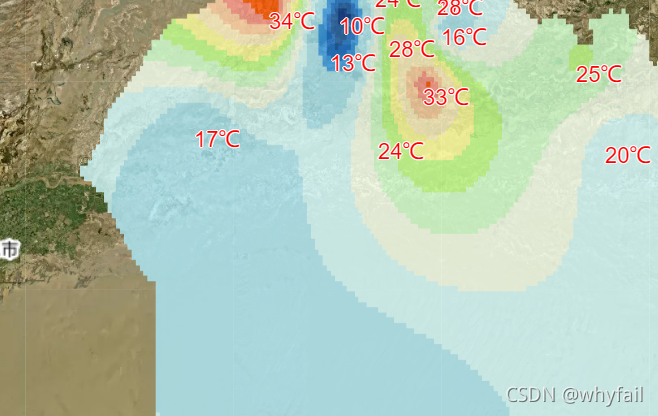
   与 ArcGIS Ordinary Kriging 插值结果（重分类后）对比：

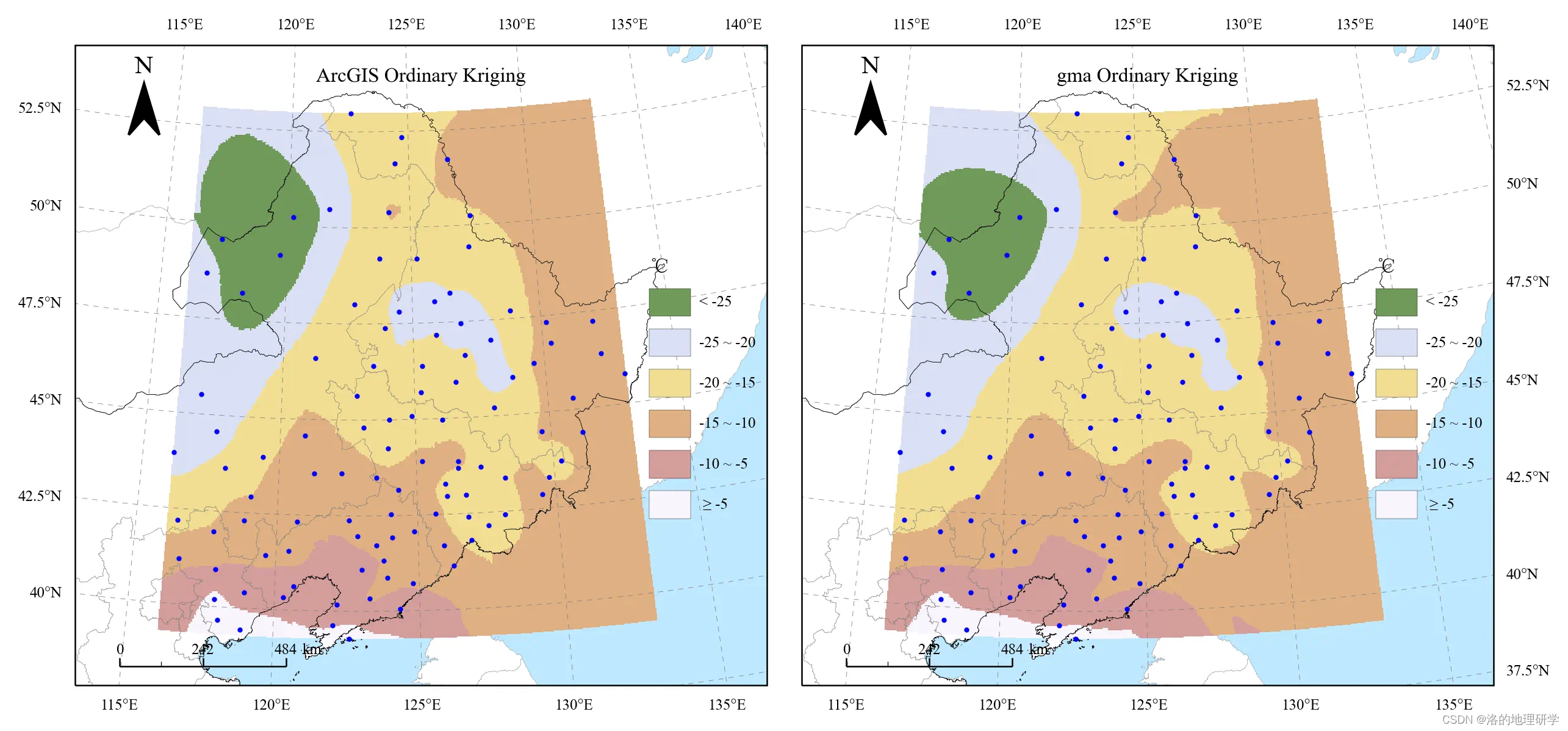
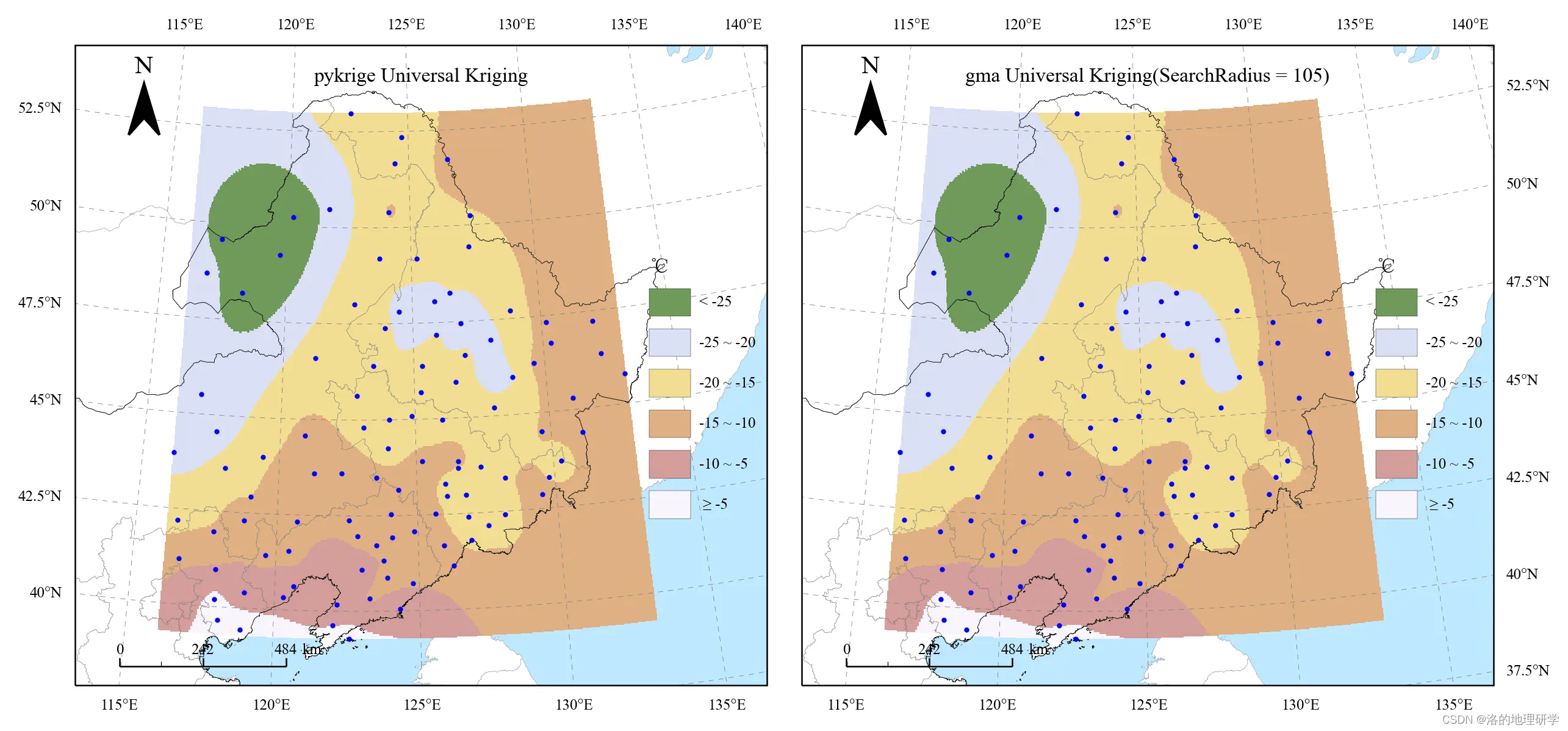
在这里插入图片描述
   与 pykrige 包 Universal Kriging 插值结果（重分类后）对比：
在这里插入图片描述


http://chatgpt.dhexx.cn/article/FmNtx2Ha.shtml

相关文章

AAAI2021论文: 时空Kriging的归纳式图神经网络

AAAI2021论文: 时空Kriging的归纳式图神经网络

1、文章信息 《Inductive Graph Neural Networks for Spatiotemporal Kriging》。麦吉尔大学发表在AAAI 2021上的一篇文章。 原文和代码链接&#xff1a; https://github.com/Kaimaoge/IGNNK 2、摘要 时间序列预测和时空Kriging是时空数据分析中最重要的两项任务。近年来&#…
阅读更多...
Cesium结合kriging.js制作降雨等值面

Cesium结合kriging.js制作降雨等值面

Cesium结合kriging.js制作降雨等值面 前因实现效果图使用克里金插值kriging.js使用方法解析 前因 因工作需要使用cesium制作降雨等值面&#xff0c;所以在参考众多博客后。终于是成功实现了降雨等值面。 参考博客&#xff1a; https://blog.csdn.net/weixin_44265800/article/…
阅读更多...
kriging及其加点准则学习

kriging及其加点准则学习

什么是加点&#xff1f; 所谓加点&#xff0c;就是给数据集增添数据点对模型进行训练。添加数据点&#xff0c;意思就是获得这个想要的数据点的真实响应&#xff0c;可以是实验的结果&#xff0c;也可以精细仿真的结果。但不管怎样&#xff0c;每增加一个数据点&#xff0c;都…
阅读更多...
openlayers加kriging出等值线图

openlayers加kriging出等值线图

openlayers加kriging出等值线图 方法一 效果图 代码 <!DOCTYPE html> <html> <head><meta charset"utf-8" /><title>前端空间插值</title><style>html, body, #map {height: 100%;width: 100%;}</style><link…
阅读更多...
leflet使用kriging.js构建气象图层

leflet使用kriging.js构建气象图层

一、克里金法 kriging.js kriging.js是一个 Javascript 库&#xff0c;通过普通克里金算法提供空间预测和映射功能。 克里金法是一种高斯过程&#xff0c;其中使用核回归将二维坐标映射到某个目标变量。该算法经过专门设计&#xff0c;可通过为变异函数参数分配先验参数来准确…
阅读更多...
Kriging(克里金模型)介绍

Kriging(克里金模型)介绍

克里金模型最早出现在地质学文献中&#xff0c;用来估计有价值矿物的分布。萨克斯艾尔1989年将这种方法应用于近似的计算机实验。此后&#xff0c;克里格法被广泛研究并应用于工程领域。 克里格模型也称为高斯过程模型&#xff0c;因为它将目标函数建模为高斯过程的实现。定义…
阅读更多...
克里金(kriging)模型的推导详解

克里金(kriging)模型的推导详解

Kriging模型理论推导 1、前言2、条件3、基础知识3.1、方差的理解3.2、概率密度函数3.3、多元正态分布 4、理论推导4.1 模型建立4.2 模型预测 1、前言 简介&#xff1a;Kriging模型是一种通过已知试验点信息来预测未知试验点上响应的无偏估计模型&#xff0c;其最早是由南非矿业…
阅读更多...
c语言函数库----＜ctype.h＞

c语言函数库----＜ctype.h＞

<ctype.h>是c标准函数库中的头文件&#xff0c;定义了一批c语言字符分类函数&#xff0c;下面将介绍<ctype.h>中的一些函数。 1、isascii()函数 isascii()函数是c语言中字符检测函数。通常用于检查参数c是否为ASCII 码字符&#xff0c;也就是判断c 的范围是否在0…
阅读更多...
C语言——标准函数库

C语言——标准函数库

<stdlib.h> 算数&#xff1a; 1、函数abs和labs返回参数的绝对值 int abs( int value ); long int labs( long int value ); 2、函数div和ldiv做除法运算 div_t div( int numerator, int denominator ); ldiv_t ldiv( long int numer, long int denom ); 函数第一个参数…
阅读更多...
Qt中调用C语言函数库

Qt中调用C语言函数库

接着上一篇文章&#xff0c;试图画出速度模型时&#xff0c;中间会有用到调用C库函数--gsl库&#xff1b;记一下怎么使用的&#xff1a; 和C语言中类似&#xff0c;但要使用到条件编译&#xff1a; #ifdef __cplusplus extern "C" { #endif #include <gsl/gsl_…
阅读更多...
c语言标准函数库怎么建立教程,C语言-基础教程-C语言函数库和文件

c语言标准函数库怎么建立教程,C语言-基础教程-C语言函数库和文件

一个函数设计完后&#xff0c;我们可以用三种方法处理它&#xff1a;1)把它放在main()函数的同一个文件中&#xff1b;2)把它和写好的其它函数一起放在另一个文件中&#xff1b;3)把它放在函数库中。下面分别讨论这三种方法。 4.6.1程序文件的大小 因为C语言允许分别编译&#…
阅读更多...
C语言字符串处理函数库

C语言字符串处理函数库

C语言的字符串处理函数库包括复制函数、拼接函数、比较函数、搜索函数等&#xff0c;这些函数的声明都位于头文件<string.h>。使用这些函数时&#xff0c;需要使用#include<string.h>指令将头文件包含到文件中。 复制函数 复制函数的功能是将字符&#xff08;节&…
阅读更多...
C语言数学函数库

C语言数学函数库

数学函数库 几乎所有语言都会提供数学函数库&#xff0c;数学函数库起码包含幂&#xff0c;对数、三角函数等最基本的运算&#xff0c;C对于基本数学函数还算全面&#xff0c;如下表&#xff1a; 使用数学函数库需要导入math.h&#xff0c;表中所有参数和返回值都是double&am…
阅读更多...
c语言常用库函数

c语言常用库函数

c语言常用库函数 1、数学函数 abs 原型&#xff1a;extern int abs(int x); 功能&#xff1a;求整数x的绝对值 说明&#xff1a;计算|x|, 当x不为负时返回x&#xff0c;否则返回-xfabs 原型&#xff1a;extern float fabs(float x); 功能&#xff1a;求浮点数x的绝对值 说明&…
阅读更多...
简单实现破解Root密码

简单实现破解Root密码

破解步骤&#xff1a; 在系统启动时进入grub选项菜单 在grub选项菜单按e进入编辑模式 编辑kernel那行 添加 /init 1 &#xff0c;相当于告诉linux下次启动启用单用户模式这个特殊模式启动。 按b重启 进入系统后&#xff0c;将root密码设置为空密码。 #vim /etc/passwd …
阅读更多...
vue-admin-beautiful-pro源码、vue admin pro、vue admin plus 基于element-plus的vue3.0 admin前端框架

vue-admin-beautiful-pro源码、vue admin pro、vue admin plus 基于element-plus的vue3.0 admin前端框架

Vue Admin Plus已拥有四种布局&#xff08;画廊布局、综合布局、纵向布局、横向布局&#xff09;四种主题&#xff08;默认、海洋之心、绿茵草场&#xff0c;荣耀典藏&#xff09;&#xff0c;共计16布局主题种组合&#xff0c;满足所有项目场景&#xff0c;已支持常规bug自动修…
阅读更多...
【Mockplus教程】安装Mockplus

【Mockplus教程】安装Mockplus

MAC上安装Mockplus 1 下载 进入摩客官网桌面端下载页面&#xff0c;选择MAC版本下载&#xff1b; 2 安装 下载完成后&#xff0c;打开dmg包&#xff0c;将Mockplus图标拖动到Applications快捷图标上面即可完成安装。 整个过程见下方视频&#xff1a; 进入摩客官网桌面端下载页面…
阅读更多...
VUE 使用 mock

VUE 使用 mock

mock使用背景 实际开发采用前后端分离形式&#xff0c;意味着后端API正在开发中&#xff0c;前端只需知道需要的数据格式即可进行开发&#xff0c;与后端开发同步进行。mock模拟后端提供api的调用&#xff0c;并返回数据。 mock使用步骤 1. 安装依赖 npm install mockjs 2…
阅读更多...
抱歉，Xposed真的可以为所欲为——5.我自己刷的Xposed凭什么不给我用

抱歉，Xposed真的可以为所欲为——5.我自己刷的Xposed凭什么不给我用

抱歉&#xff0c;Xposed真的可以为所欲为——5.我自己刷的Xposed凭什么不给我用 标签&#xff1a; 2018 一句话概括本文 分析定位排查下厨房APP检测手机是否安装了Xposed框架的方法&#xff0c;然后一步步 Hook掉对应代码&#xff0c;以此去掉恶心的重复弹出警告对话框。 引…
阅读更多...
2022最新 vue中mock的使用步骤 亲测可用

2022最新 vue中mock的使用步骤 亲测可用

第一步&#xff1a;在src目录下创建文件夹mock&#xff0c;mock下创建文件index.js存放mock数据 index.js代码&#xff1a; import Mock from "mockjs" // const chartData { // "Msg": "success", // "ResCode": 200, // …
阅读更多...
推荐文章

Copyright @ 2022~2023