AAAI2021论文: 时空Kriging的归纳式图神经网络

1、文章信息

《Inductive Graph Neural Networks for Spatiotemporal Kriging》。麦吉尔大学发表在AAAI 2021上的一篇文章。

原文和代码链接：

https://github.com/Kaimaoge/IGNNK

2、摘要

时间序列预测和时空Kriging是时空数据分析中最重要的两项任务。近年来，GNN在时间序列预测方面取得了长足的进展，但对于Kriging问题——恢复未采样位置或传感器的信号的研究却很少。大多数现有的可扩展Kriging方法(例如，矩阵/张量补全)是Transductive learning（直推式学习），因此当一个新的传感器要插入时，需要再训练。本文提出了一个归纳图神经网络Kriging——Inductive Graph Neural Network Kriging (IGNNK) 模型恢复图/网络中未采样的传感器数据。为了泛化距离和可达性的影响，本文生成随机子图作为样本，并对每个样本重构邻接矩阵。通过泛化每个样本子图上的所有信号，IGNNK可以有效地学习空间消息传递机制。在真实时空数据集上证明了提出的模型的有效性。此外，本文还发现学习到的模型可以成功地转移到看不见的数据上的相同类型的Kriging任务。实验结果表明: (1) GNN是一种有效的空间Kriging方法；(2) 归纳式GNN可用于动态邻接矩阵训练；(3) 经过训练的模型可以转化为新的图结构；(4) 提出的 IGNNK可以生成虚拟传感器。

3、动机

(1) 对于一般的时空Kriging问题（例如在欧几里得域中），一种方法是高斯过程回归，它使用灵活的核结构来表征时空相关性，但有两个局限性：1) 该模型计算量大，因此无法处理大规模数据集；2) 难以使用现有的图核 (Graph kernal) 建模网络系统。为了解决网络系统中的大规模Kriging问题，图正则化的矩阵/张量补全已成为一种有效的解决方案。这些模型结合了低秩结构和时空图正则化方法，可以同时表征数据的全局一致性和局部一致性。然而，矩阵/张量补全本质上是直推式学习。对于引入到网络中的新传感器/节点，本文不能直接应用先前训练过的模型。相反，本文必须为新的图结构重新训练完整的模型，即使只有很小的变化(即在引入一个新的传感器后)。另外，低秩方案不能适应时变/动态图结构。

(2) 最近的研究使用GNN对时空数据进行建模。GNN通过其消息传递机制在表征复杂的空间依赖性方面具有强大的功能。它们还展示了将消息传递机制推广到看不见的节点甚至是全新的子图上的能力和归纳式能力。受这些工作的启发，本文提出了一个归纳图神经网络Kriging（IGNNK）模型，以解决动态网络结构上的实时时空Kriging问题。与推荐系统中的图不同，本文的空间图实际上包含有价值的位置信息，这使本文可以量化除“hops”之外的成对“距离”。特别地，对于诸如高速公路网络的有向网络，距离矩阵将是不对称的，并且实际上捕获了从一个传感器到另一个传感器的“可达性”程度。

4、问题定义

时空Kriging是指在未采样传感器位置给定从采样传感器位置得到的信号后，对时间序列信号进行插值的任务。本文的重点是网络上的时空Kriging：空间域由二维平面变为不规则的网络结构。以高速公路网络上的一组交通传感器为例：本文可以将传感器建模为网络中的节点，并且可以根据高速公路网络的类型定义网络的边。在这种情况下，时空Kriging的目标是恢复无传感器位置的交通状态时间序列。因此，Kriging可以看作是建立虚拟传感器的过程。

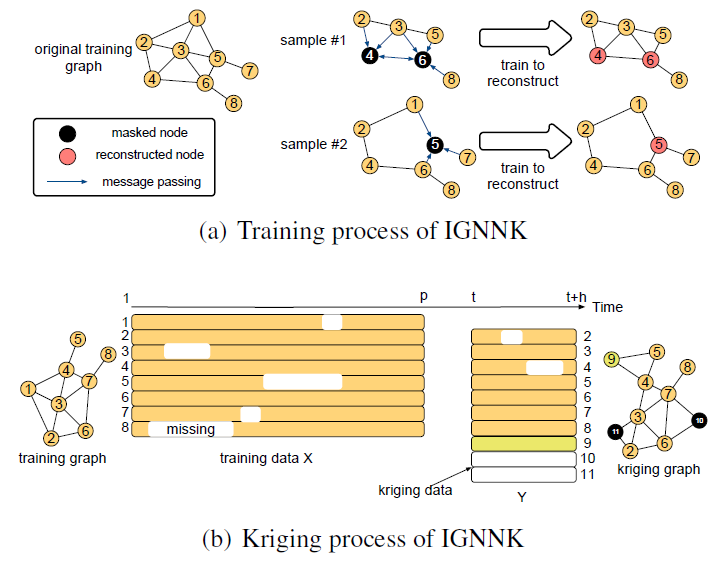
图1 IGNNK的Kriging过程

本文在图1(b) 中说明了实时的Kriging过程，假设本文有 n=8 个在[1, p ]时间段内的传感器，本文用多元时间序列矩阵表示可用的训练数据，每一行为传感器采集的信号。有来自个传感器的数据，对应传感器 {2,…,9}，本文旨在个虚拟传感器（例如，新的或未采样的节点，对应图1(b)中的传感器{10,11}）上的插值信号。总之，本文的目标是给定估计。

5、模型

(1) 子图信号和随机掩码

本文使用一个随机抽样程序来生成一组用于训练的子图。其核心思想是随机抽样一个节点子集得到，并建立相应的邻接矩阵。在空间设置中，本文的图基本上是完全连通的，本文期望边权值随着一对节点之间的欧氏/出行距离而减小。为了更好地描述“距离”的影响，本文简单地选择一个纯随机抽样方案来生成样本子图，而不是为每个节点创建一个局部子图。本文创建一个掩模矩阵，以使某些节点保持观察状态，而测试保持“未采样”状态。然后使用生成的掩码M、图信号X和邻接矩阵来训练GNN。由于无法准确地知道测试节点的空间位置，因此随机生成了，使学习样本可以泛化到更多的案例中。输入数据本身可能包含缺失的值，本文也将其标记为未知值。这将使IGNNK能够在缺少数据的场景下执行空间插值。

(2) GNN结构

给定不完整的信号：

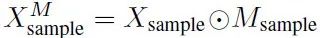
训练一个GNN模型来重构子图上的完整矩阵X。

为了表征空间和方向依赖性的随机性质，采用DCRNN中的扩散图卷积（DGCN）作为本文结构的基本构建块。与使用固定空间结构的传统GNN不同，在IGNNK中，每个样本都有其自己的子图结构。因此，捕获邻域信息和消息传递方向的邻接矩阵W在不同的样本中也不同。图2说明了IGNNK的GNN结构，它是一个简单的3层DGCN。

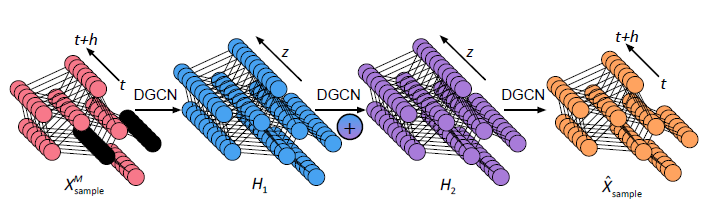
图2 IGNNK中GNN结构

第一次的输入是掩码信号

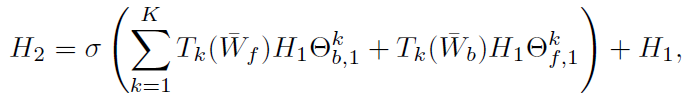
本文将添加到的原因是包含有关缺少数据的传感器的信息。

在获得最终的图表示之后，本文使用另一个DGCN输出重构：

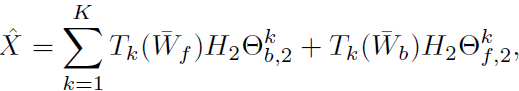
(3) 损失函数

从方法论的角度来看，本文倾向于将IGNNK推广到动态图结构和看不见的节点。为了使学习到的消息传递机制对所有节点更加通用，使用观测节点和看不见的节点上的总重构误差作为损失函数:

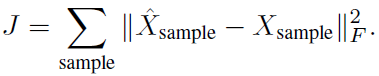
6、数值实验

本文使用了5个数据集：

(1) METR-LA：四个月（2012年3月1日至2012年6月30日）洛杉矶207个传感器的交通速度数据集。

(2) NREL：2006年阿拉巴马州137个光伏发电厂的太阳能输出。

(3) USHCH：1899 - 2019年，1218个地点的月降水量。

(4) SetData：从西雅图公路网的323个环路检测器收集的交通速度数据集。

(5) PeMS-Bay：从2017年1月1日到2017年5月13日湾区325个传感器的交通速度时间序列。

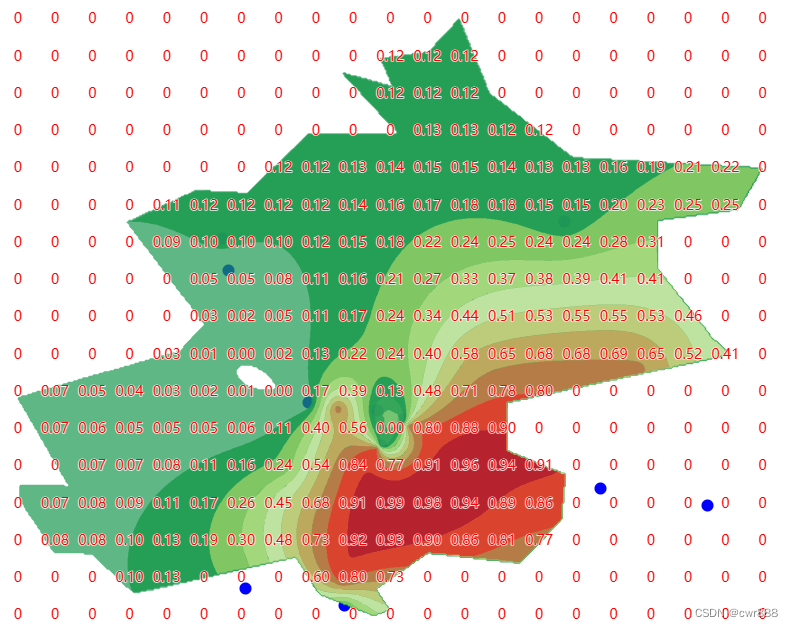
本文选择RMSE、MAE和R2三个评价指标。在图3中提供了一个关于IGNNK和其他对比模型的空间可视化的例子。可以看出，与kNN和GLTL相比，IGNNK的重构更接近ground truth。

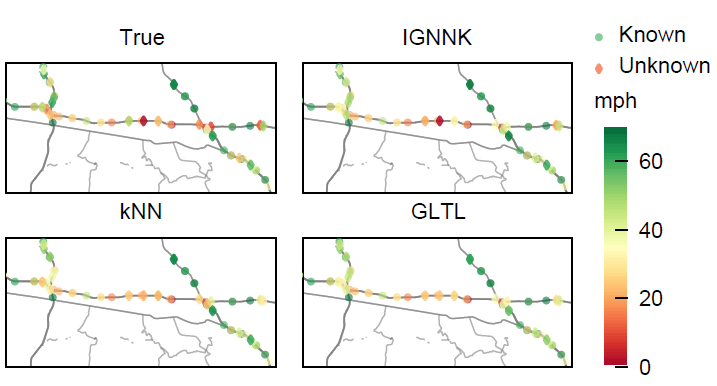
图3 METR-LA数据集在拥挤的晚高峰时间点(2012-05-22 17:45) 的Kriging空间表示。Ground truth、IGNNK、kNN和GLTL的速度值分别显示在左上角、右上方、左下角和右下角

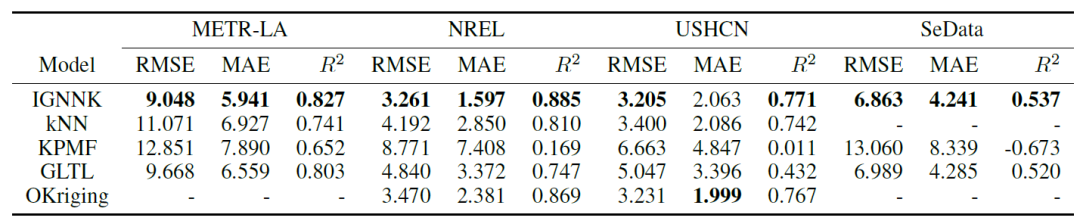
表1 不同模型在4个数据集上的Kriging性能比较

除此之外，本文还分析了PeMSBay数据集未知节点的Kriging性能、PeMS-Bay数据集上不同模型的Kriging性能。可视化了虚拟传感器上的Kriging结果。

6、结论

本文中介绍了IGNNK作为Kriging的新框架。该训练方案为IGNNK提供了额外的推广和归纳式能力，而不是直推的潜在特征。因此，本文可以直接应用经过训练的模型来对任何新的感兴趣位置执行Kriging，而无需重新训练。数值实验表明，IGNNK在五个真实的时空数据集上始终优于其他对比模型。此外，IGNNK在交通数据Kriging任务示例中演示了显著的可移植性。实验结果还表明，图中的“距离”信息在Kriging中起着至关重要的作用，这与推荐系统中的应用不同，在推荐系统中图本质上是编码拓扑信息。IGNNK的灵活性能够为时变系统建模，例如移动传感器（例如探测车）或众包系统，这将创建动态网络结构。

未来的工作有几个方向。首先，可以使用IGNNK作为时空张量来适应多元数据集。其次，更好的时间模型，如RNNs和TCNs，以表征复杂的时间依赖性。这将使得在更长的时间窗口内执行Kriging成为可能，并具有更好的时间动态。第三，可以进一步将时间序列预测与Kriging结合在一个集成的框架中，为现有和虚拟传感器提供预测结果，以更好地制定决策。