目录

二叉树的改进---红黑树

红黑树和AVL树（平衡二叉树）区别

---

 

确实是AVL（平衡二叉树）更严格（左右子树树高不超过1）, 红黑树只保证最长路径不超过最短路径的2倍

 

二叉树的改进---红黑树

这个是一个 小灰程序员 的作品，可以关注他的公众号。

 

……省略多图……

 

 

二叉查找树（BST）具备什么特性呢？

 

1.左子树上所有结点的值均小于或等于它的根结点的值。

2.右子树上所有结点的值均大于或等于它的根结点的值。

3.左、右子树也分别为二叉排序树。

 

下图中这棵树，就是一颗典型的二叉查找树：

 

 

1.查看根节点9：

 

 

2.由于10 > 9，因此查看右孩子13：

 

 

3.由于10 < 13，因此查看左孩子11：

 

 

4.由于10 < 11，因此查看左孩子10，发现10正是要查找的节点：

 

 

 

 

 

 

 

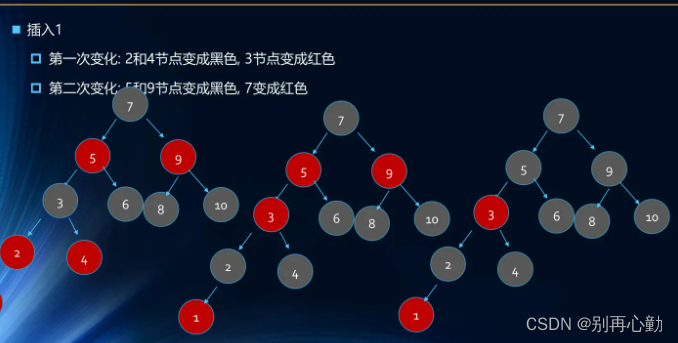
假设初始的二叉查找树只有三个节点，根节点值为9，左孩子值为8，右孩子值为12：

 

 

接下来我们依次插入如下五个节点：7,6,5,4,3。依照二叉查找树的特性，结果会变成什么样呢？

 

 

 

 

 

 

红黑树---------一种自平衡的 二叉查找树 

1.节点是红色或黑色。

2.根节点是黑色。

3.每个叶子节点都是黑色的空节点（NIL节点）。

4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

 

下图中这棵树，就是一颗典型的红黑树：

 

 

 

 

 

 

什么情况下会破坏红黑树的规则，什么情况下不会破坏规则呢？我们举两个简单的栗子：

 

1.向原红黑树插入值为14的新节点：

 

 

2.向原红黑树插入值为21的新节点：

 

 

由于父节点22是红色节点，因此这种情况打破了红黑树的规则4（每个红色节点的两个子节点都是黑色），必须进行调整，使之重新符合红黑树的规则。

 

 

 

变色：

 

为了重新符合红黑树的规则，尝试把红色节点变为黑色，或者把黑色节点变为红色。

 

下图所表示的是红黑树的一部分，需要注意节点25并非根节点。因为节点21和节点22连续出现了红色，不符合规则4，所以把节点22从红色变成黑色：

 

 

 

但这样并不算完，因为凭空多出的黑色节点打破了规则5，所以发生连锁反应，需要继续把节点25从黑色变成红色：

 

 

此时仍然没有结束，因为节点25和节点27又形成了两个连续的红色节点，需要继续把节点27从红色变成黑色：

 

（左旋右旋说明：https://www.jianshu.com/p/e136ec79235c）

左旋转：

左旋：以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。如图3。

逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己成为自己的左孩子。说起来很怪异，大家看下图：

 

 

图中，身为右孩子的Y取代了X的位置，而X变成了自己的左孩子。此为左旋转。

 

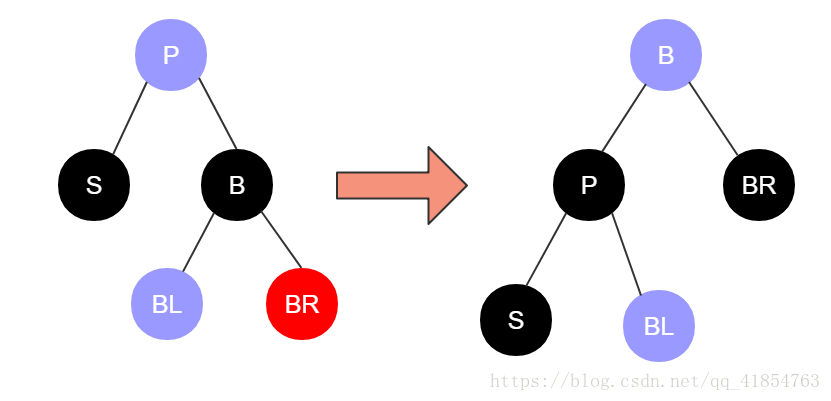
右旋转：

右旋：以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。

顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子。大家看下图：

 

 

图中，身为左孩子的Y取代了X的位置，而X变成了自己的右孩子。此为右旋转。

 

 

 

我们以刚才插入节点21的情况为例：

 

 

首先，我们需要做的是变色，把节点25及其下方的节点变色：

 

 

此时节点17和节点25是连续的两个红色节点，那么把节点17变成黑色节点？恐怕不合适。这样一来不但打破了规则4，而且根据规则2（根节点是黑色），也不可能把节点13变成红色节点。

 

变色已无法解决问题，我们把节点13看做X，把节点17看做Y，像刚才的示意图那样进行左旋转：

 

 

 

 

由于根节点必须是黑色节点，所以需要变色，变色结果如下：

 

 

这样就结束了吗？并没有。因为其中两条路径(17 -> 8 -> 6 -> NIL)的黑色节点个数是4，其他路径的黑色节点个数是3，不符合规则5。

 

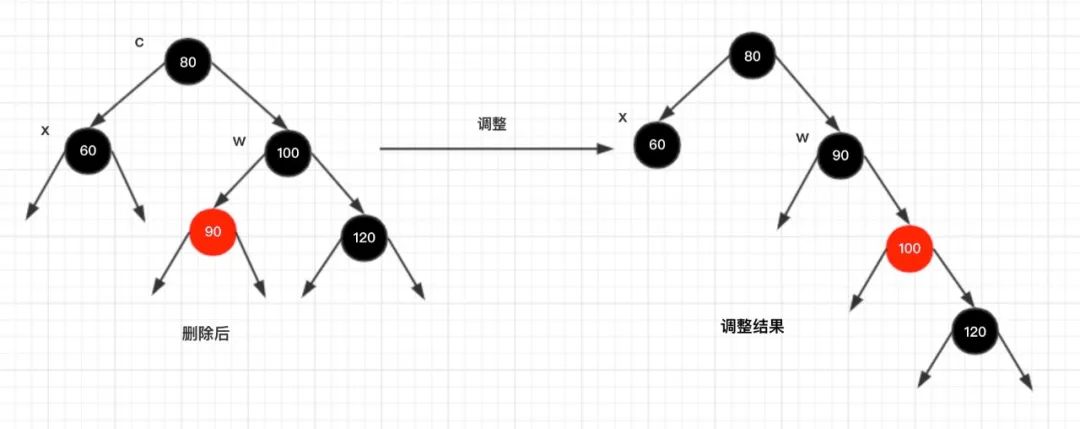
这时候我们需要把节点13看做X，节点8看做Y，像刚才的示意图那样进行右旋转：

 

 

 

 

最后根据规则来进行变色：

 

 

如此一来，我们的红黑树变得重新符合规则。这一个例子的调整过程比较复杂，经历了如下步骤：

 

变色 -> 左旋转 -> 变色 -> 右旋转 -> 变色

 

 

 

 

 

几点说明：

 

1. 关于红黑树自平衡的调整，插入和删除节点的时候都涉及到很多种Case，由于篇幅原因无法展开来一一列举，有兴趣的朋友可以参考维基百科，里面讲的非常清晰。

 

2.漫画中红黑树调整过程的示例是一种比较复杂的情形，没太看明白的小伙伴也不必钻牛角尖，关键要懂得红黑树自平衡调整的主体思想。

 

 

红黑树和AVL树（平衡二叉树）区别

本文转载至链接：https://blog.csdn.net/u010899985/article/details/80981053

一、AVL树(平衡二叉树)

(1)简介

AVL树是带有平衡条件的二叉查找树，一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡，左右子树高度差不超过1，和红黑树相比，AVL树是严格的平衡二叉树，平衡条件必须满足(所有结点的左右子树高度差不超过1)。不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保存平衡，而因为旋转非常耗时，由此我们可以知道AVL树适合用于插入与删除次数比较少，但查找多的情况。

(2)局限性

由于维护这种高度平衡所付出的代价比从中获得的效率收益还大，故而实际的应用不多，更多的地方是用追求局部而不是非常严格整体平衡的红黑树。当然，如果应用场景中对插入删除不频繁，只是对查找要求较高，那么AVL还是较优于红黑树。

(3)应用

1.Windows NI内核中广泛存在;

二、红黑树

(1)简介

一种二叉查找树，但在每个节点增加一个存储位表示结点的颜色，可以是红或黑(非红即黑)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，因此，红黑树是一中弱平衡二叉树(由于是弱平衡，可以看到，在相同的节点情况下，AVL树的高度低于红黑树)，相对于要求严格的AVL树来说，它的旋转次数少，插入最多两次旋转，删除最多三次旋转，所以对于搜索，插入，删除操作较多的情况下，我们就用红黑树。

(2)性质

(1)结点非红即黑

(2)根结点是黑色的

(3)每个叶子节点(NULL节点)是黑色的

(4)每个红色节点的两个子节点都是黑色的。(不能有两连续的红色节点)

(5)从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

注意：性质(5)保证红黑树的最长路径不超过最短路径的两倍。

(3)应用

1、广泛应用于C++的STL中，map和set底层都是用红黑树实现的。

 

 

漫画算法系列

 

• 漫画算法：最小栈的实现

• 漫画算法：判断 2 的乘方

• 漫画算法：找出缺失的整数

• 漫画算法：辗转相除法是什么鬼？

• 漫画算法：什么是动态规划？（整合版）

• 漫画算法：什么是跳跃表？

• 漫画算法：什么是 B 树？

• 漫画算法：什么是 B+ 树？

• 漫画算法：什么是一致性哈希？

• 漫画算法：无序数组排序后的最大相邻差值

• 漫画算法：什么是 Bitmap 算法？

• 漫画算法：Bitmap算法（进阶篇）

• 漫画算法：什么是布隆算法？

• 漫画算法：什么是 A* 寻路算法？

• 漫画算法：什么是 Base64 算法？

• 漫画算法：什么是 MD5 算法？

• 漫画算法：如何破解 MD5 算法？

• 漫画算法：什么是 SHA 系列算法？

• 漫画算法：什么是 AES 算法？

• 漫画算法：AES 算法的底层原理

转自：https://blog.csdn.net/p5deyt322jacs/article/details/78433942