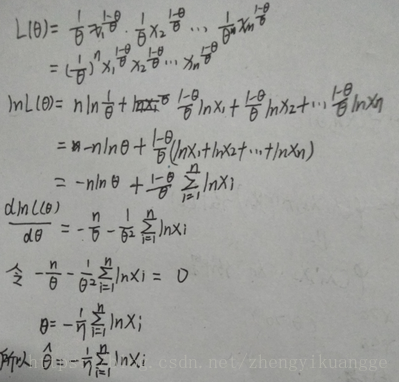【数据统计】— 峰度、偏度、点估计、区间估计、矩估计、最小二乘估计
- 四分位差
- 异众比率
- 变异系数
- 利用数据指标指导建模思路
- 形状变化
- 数据分布形态
- 峰度: 度量数据在中心聚集程度
- 偏度
- 利用数据指标指导建模思路
- 参数估计
- 点估计
- 区间估计
- 矩估计
- 举例:黑白球(矩估计)
- 最小二乘估计(Least Square Estimate, LSE)
- 举例:黑白球(最小二乘估计)
四分位差
- 一组数据的上四分位数和下四分位数的差,也称为内矩
- 若上四分位数为𝑄𝑈,下四分位数为𝑄𝐿,则四分位差为

- 特点
- Q是区间[𝑄𝐿, 𝑄𝑈]的长度
- 区间[𝑄𝐿, 𝑄𝑈]含有50%的数据
- 四分位数不会受到数据中极端值的影响

异众比率

变异系数

利用数据指标指导建模思路
- 若均值与中位数接近,且偏度接近0,可知数据分布是近似对称的,建模时可考虑运用对称信息。
- 若极差或四分位差较大,建模时需考虑数据是否有长尾现象

形状变化
数据分布形态
- 数据分布形态反映了一组数据分布的整体形状信息。
- 两种最常用的反映数据形状变化的指标:
- 峰度
- 偏度
峰度: 度量数据在中心聚集程度
- 峰度(Kurtosis)是描述总体中所有取值
分布形态陡峭程度 or 平坦程度 - 峰度的具体计算公式为:

- 正态分布的峰度值为3
- 个别软件将峰度值减3, 如:SPSS等
- 与正态分布相比较
- 峰度=0表示该总体数据分布与正态分布的陡缓程度相同
- 峰度>0表示该总体数据分布与正态分布相比较为陡峭,为尖顶峰
- 峰度<0表示该总体数据分布与正态分布相比较为平坦,为平顶峰

偏度
-
偏度(Skewness)描述的是某总体取值分布的对称性
-
偏度的具体计算公式为:

-
正态分布的偏度值为0
-
某个总体
- 偏度=0表示数据分布形态与正态分布的偏斜程度相同
- 偏度>0表示数据分布形态与正态分布相比为正偏或右偏,即有一条长尾巴拖在右边,数据右端有较多的极端值
- 偏度<0表示数据分布形态与正态分布相比为负偏或左偏,即有一条长尾拖在左边,数据左端有较多的极端值。

利用数据指标指导建模思路
- 峰度的应用
- 正态分布
- 拉普拉斯分布:更好的拟合0出现概率较大的稀疏数据

- 泊松分布:
- 例如,POI(兴趣点)位置的访问频率
- 幂律分布:对数空间下呈现出线性关系(80-20法则)
- 例如:社交网络(Social Network), 图网络分析


- 例如:社交网络(Social Network), 图网络分析
参数估计
- 参数(parameter)
- 参数 是用来描述总体数据特征的度量
- 统计量(statistic)
- 统计量 是用来描述样本数据特征的度量
- 由试验计算得出,不依赖于任何其他未知的量(特别是不能依赖于总体分布中所包含的未知参数)
- 统计量 是用来描述样本数据特征的度量
- 参数估计(parameter estimation)
- 是统计推断的基本问题之一:用样本统计量估计总体的参数
- 参数未知的真实
- 统计量已知的估计
- 例:掷骰子例子
- 是统计推断的基本问题之一:用样本统计量估计总体的参数
点估计
- 点估计:用样本统计量𝜃 的某个取值直接作为总体参数𝜃的估计值
- 简单来说,直接以样本指标来估计总体指标
- 总体的某个特征值,如数学期望、方差和相关系数等
- 用样本均值 x x x直接作为总体均值 μ μ μ的估计值
- 用样本方差 s 2 s^2 s2直接作为总体方差 σ 2 σ^2 σ2的估计值
- 点估计的常用方法
- 矩估计
- 最小二乘估计
- 极大似然估计
- 最大后验概率
- 贝叶斯估计
区间估计
- 区间估计:从总体中抽取的样本,根据一定的正确度与精确度的要求,构造出适当的区间,以作为总体的分布参数(或参数的函数)的真值所在范围的估计
- 用数轴上的一段经历或一个数据区间,表示总体参数的可能范围。这一段距离或数据区间称为区间估计的置信区间
矩估计
-
原理:大数定律(大量试验中的事件出现频率=它的概率)
-
矩估计是基于 “替换”思想,即用样本矩估计总体矩
- 均值,方差
-
随机变量的矩
- K阶原点矩:一阶原点矩表示期望

- K阶中心距:

- 二阶中心矩表示方差
- 三阶中心矩表示偏度
- 四阶中心矩表示峰度

- K阶原点矩:一阶原点矩表示期望
-
数学上,“矩”是一组点组成的模型的特定的数量测度
举例:黑白球(矩估计)
- 例:假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。每次任意从已经摇匀的罐中拿1个球出来,记录球的颜色,然后把拿出来的球再放回罐中。假如在前面的100次重复记录中,有70次是白球。请问罐中白球所占的比例是多少?
- 解:用样本中白球比例的均值作为估计代替总体均值。即估计结果为罐中白球所占的比例70% =7/10。符合直观
最小二乘估计(Least Square Estimate, LSE)
- 参数估计量应该使得模型能最好地拟合样本数据,即估计值与观测值之差的平方和最小
- 目标:最小化估计值𝑦与观测值 y ^ \hat{y} y^之差的平方和 m i n L ( θ ) = ∑ i = 1 N ( y − y ^ ) 2 min L(θ)=\sum^N_{i=1}(y-\hat{y})^2 minL(θ)=i=1∑N(y−y^)2



举例:黑白球(最小二乘估计)
- 问题:假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。每次任意从已经摇匀的罐中拿1个球出来,记录球的颜色,然后把拿出来的球再放回罐中。假如在前面的100次重复记录中,有70次是白球。请问罐中白球所占的比例是多少?
- 请使用最小二乘估计方法,求解上述问题