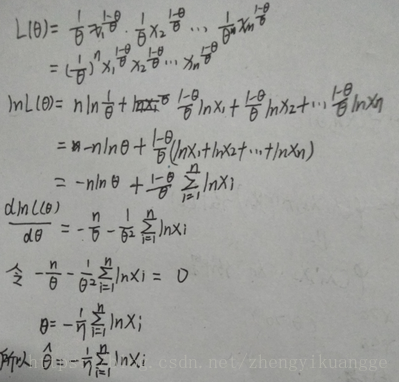1 基础知识
1.1 常见分布的期望和方差

1.2 对数运算法则
log a ( M N ) = log a M + log a N log a ( M / N ) = log a M − log a N log a ( 1 / N ) = − log a N log a M n = n log a M \log _{a}(M N)=\log _{a} M+\log _{a} N \\ \log _{a}(M / N)=\log _{a} M-\log _{a} N \\ \log _{a}(1 / N)=-\log _{a} N \\ \log _{a} M^{n}=n \log _{a} M loga(MN)=logaM+logaNloga(M/N)=logaM−logaNloga(1/N)=−logaNlogaMn=nlogaM
1.3 矩
参考第三篇链接文章,内含具体示例,值得一看!

| 名称 | 含义 |
|---|---|
| 一阶原点矩 | 平均值 |
| 二阶原点矩 | 平均能量 |
| 一阶中心距 | 0 |
| 二阶中心距 | 方差 |
| 三阶中心距 | 偏度 |
| 四阶中心距 | 峭度 |
2 点估计与矩估计
起初,我以为点估计和矩估计可能是相对的概念,其实矩估计方法是点估计中的一种,其原理就是构造样本和总体的矩,然后用样本的矩去估计总体的矩。
2.1 什么是点估计?
设总体 X的分布函数的形式已知,但它的一个或多个参数未知,借助于总体的一个样本来估计总体未知参数的值的问题称为参数的点估计问题。
2.2 矩估计法
设 X 是一随机变量,若 E ( X k ) E\left(X^{k}\right) E(Xk)存在,则称它为 X 的 k 阶原点矩,简称 k 阶矩。
我们称 A k = 1 n ∑ i = 1 n X i k A_{k}=\frac{1}{n} \sum_{i=1}^{n} X_{i}^{k} Ak=n1∑i=1nXik为样本 k 阶矩。样本 k 阶矩 A_{k} 是 k 阶总体矩 μ k = E ( X k ) \mu_{k}=E\left(X^{k}\right) μk=E(Xk) 的无 偏估计量。这也正是矩估计法的原理。
设 X 为连续型随机变量,概率密度为 f ( x ; θ 1 , ⋯ , θ k ) f\left(x ; \theta_{1}, \cdots, \theta_{k}\right) f(x;θ1,⋯,θk); 或 X 为离散型随机变量,其分布 律为 P { X = x } = p ( x ; θ 1 , ⋯ , θ k ) P\{X=x\}=p\left(x ; \theta_{1}, \cdots, \theta_{k}\right) P{X=x}=p(x;θ1,⋯,θk)。 θ 1 , ⋯ , θ k \theta_{1}, \cdots, \theta_{k} θ1,⋯,θk 为待估参数, X 1 , ⋯ , X n X_{1}, \cdots, X_{n} X1,⋯,Xn 是来自 X 的样本。 假设总体 X 的前 k 阶矩为:
μ l = E ( X l ) = ∫ − ∞ ∞ x l f ( x ; θ 1 , ⋯ , θ k ) d x ( 连续型 ) \mu_{l}=E\left(X^{l}\right)=\int_{-\infty}^{\infty} x^{l} f\left(x ; \theta_{1}, \cdots, \theta_{k}\right) d x \quad(\text { 连续型 }) μl=E(Xl)=∫−∞∞xlf(x;θ1,⋯,θk)dx( 连续型 )
或
μ l = E ( X l ) = ∑ x l p ( x ; θ 1 , ⋯ , θ k ) ( 离散型 ) \mu_{l}=E\left(X^{l}\right)=\sum x^{l} p\left(x ; \theta_{1}, \cdots, \theta_{k}\right) \quad(\text { 离散型 }) μl=E(Xl)=∑xlp(x;θ1,⋯,θk)( 离散型 )
通过式子可以看出,前 k 阶矩是对于 θ 1 , ⋯ , θ \theta_{1}, \cdots, \theta θ1,⋯,θ 的函数。而样本 k 阶矩是 k 阶矩的无偏估 计,故我们可以得到思路:
- 假设我们有 k 个待估参数,连立1阶矩、2阶矩、直到 k 阶矩,我们就得到了 k 个方程, k 个末知量 (待估参数) ;
- 解得每个待估参数,接着用样本 k 阶矩替换 k 阶矩即完成估计。
例题

3 最大似然估计
极大似然估计,通俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值!
换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。
3.1离散

3.2连续

很多情况下, p ( x ; θ ) p(x;\theta) p(x;θ)和 f ( x ; θ ) f(x;\theta) f(x;θ)都关于 θ \theta θ可微,所以可通过方程:
d d θ L ( θ ) = 0 \frac{\mathrm{d}}{\mathrm{d}\theta}L(\theta)=0 dθdL(θ)=0
求出最大似然估计值 θ ^ \hat\theta θ^,又因为 L ( θ ) L(\theta) L(θ)和 ln L ( θ ) \ln L(\theta) lnL(θ)在同一个 θ \theta θ处取得极值,所以也可以通过解:
d d θ ln L ( θ ) = 0 \frac{\mathrm{d}}{\mathrm{d}\theta}\ln L(\theta)=0 dθdlnL(θ)=0
求出最大似然估计值\hat\theta,由于对数可以将乘法转为加法,所以求解该方程可能会简单些。 ln L ( θ ) \ln L(\theta) lnL(θ)也称为 \color{Salmon} 对数似然函数。
还需要补充一下,首先,最大似然估计值 θ ^ \hat\theta θ^往往(符合某些条件时,在实践中可以认为基本都是符合条件的)是一致的,因此是可以接受的估计量;其次,似然函数和概率函数最大的不同,前者的自变量为参数,参数是确定的值,并非是随机变量,而概率函数的自变量为随机变量。
3.3 例题


References
1、点估计及矩估计的一些理解_huguozhiengr的博客
2、参数估计(一).矩估计法 - 知乎 (zhihu.com)
3、概率论中的“矩”是什么意思
4、一文搞懂似然估计