- 概述
- 频分复用(Frequency Division Multiplexing)
- 时分复用(Time Division Multiplexing)
- 波分复用(Wave Division Multiplexing)
- 码分复用(Code Division Multiplexing)
概述
数据是在物理链路的信道中传输的,通常一条链路上会有多条信道。在默认情况下,一条信道只传输一路信号,这就有可能造成信道带宽的浪费。就如同一条10m宽的车道,如果不划分子车道,必然就会使该道路的效率下降,实际上除了划分车道还有很多其他的方式来提升其效率。
对于计算机网络的数据传输也是一样的,可以将一条高带宽的信道划分成多条小带宽的子信道,这样就可以同时进行多路带宽需求低的数据传输,提升信道的利用率。这种技术就叫做信道复用(Channet Multiplexing)技术。
信道复用主要有如下技术:
- 频分复用(FDM, Frequency Division Multiplexing)
- 时分复用(TDM, Time Division Multiplexing)
- 波分复用(WDM, Wave Division Multiplexing)
- 码分复用(CDM, Code Division Multiplexing)
频分复用(Frequency Division Multiplexing)
按照信道频带宽度进行复用,是调制技术的一种,也就是把一条高带宽的信道按照频带再次划分成若干个低带宽的子频带(信道)。如一个1\~10MHz的信道,如果需要划分成4个子信道,则可划分成1\~2.5、2.52\~5.0、5.02\~7.5、7.52\~10.0Mhz的4个子信道。
图片来自《深入理解计算机网络》
其基本原理就和车道划分一样,将可用车道(信道)划分成若干个不交叠的子车道(子信道)。这样汽车(信号)就可以在子车道(子信道)中互不干扰的行使(传输)了。
但在FDM中,为了防止相邻子信道传输的信号互相干扰,不仅子信道之间载波频带是完全分隔的,而且子信道间最好也有一定的间隙,所以FDM对频带的利用率是相对较低的,但复用路数不是很多时可以考虑。
它优点在于复用率高,实现简单,是模拟通信中常采用的一种方式。而缺点则是容易出现干扰,主要原因是滤波器特性不理想,容易出现非线性造成的信号频谱展宽。
还有一种新的方式——正交频分复用(OFDM, Orthogonal Frequency Division Multiplexing),通过将数据流分解成为若干子信道流,将单信道流传输调制为多信道流的并行传输,也就是多载波调制(MCM, Multi-Carrier Modulation),正交指的是载波信号频谱是正交的,即载波频谱可以有交叉,但不能重叠,通过某种技术实现分离。由于载波可以交叉,无需保护频带,这样频谱的使用效率更高,比FDM要求的信道带宽小的多,另外OFDM可动态分配子信道中的数据来提升数据吞吐量。
时分复用(Time Division Multiplexing)
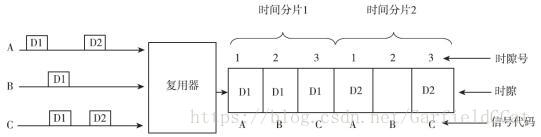
FDM是出于单一数据无法占用整条带宽,浪费了信道资源考虑的。而时分复用则是出于单个用户不可能总是有数据在传输,总是有无数据传输的空闲时段的考虑,将信息传输过程划分为一个个时间片,而时间片中在划分为更小的时隙,每个时隙对应一个用户的传输,这样就可以使得每个时间片中总有一个或多个时隙在传输数据(因为不太可能多路信号同时没有数据传输),以此实现提高信道利用率。
图片来自《深入理解计算机网络》
如上图所示,先把整个数据传输过程划分成时间片,时间片中又划分成时隙,分别用于传输三路信号。
时分复用是建立在采样定理的基础上,因为采用定理使连续的信号变成时间上的离散脉冲,当采样脉冲占据时间较短时就留出了时隙。因为时分复用以时间作为信号分割的参量,所以各路信号在时间轴上不能重叠,又由于每路数据总是用每个时间片的固定时隙,所以这种复用过程又称作同步时分复用。
通过这种原理可以看出,尽管划分成小的时隙可以提高信道的利用率,但还是会存在一些问题,如某路信号无数据传输,但其他路信号也无法占用该路信号的时隙进行传输。所以又有一种改进型的TDM——统计时分复用(STDM, Statistical Time Division Multiplexing),它也称作异步时分复用,是一种可以动态分配时隙的时分复用,使用按需分配的技术来减少空闲时隙。
波分复用(Wave Division Multiplexing)
波分是针对光信号的频分复用技术(FDM是针对电信号的),所以又称作光波分复用,是在单条光纤中同时发送多束波长不一的光信号的技术。不同的光纤波长并不一致,绝大多数是不能完全占用整条光纤的带宽的。在以前不采用WDM技术的光纤连接中,收、发要用两条光纤,而新型光纤连接都支持WDM,只需一条光纤即可实现双工工作。
图片来自《深入理解计算机网络》
码分复用(Code Division Multiplexing)
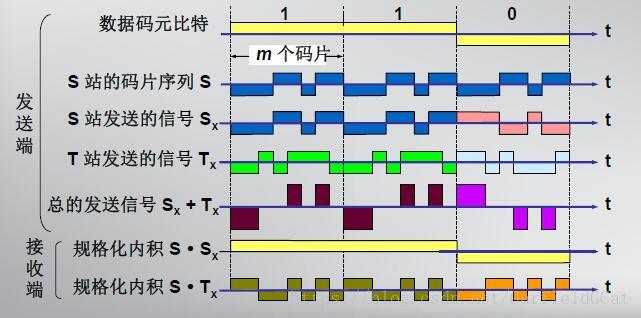
码分复用是通过不同编码来区分各路原始信号的一种复用方式,和各种多址技术结合产生很多接入技术,最常见的码分多址(CDMA)即是其中一种。
码分多址为每个用户分配各自特定的码片(地址码),然后利用公共信道来传输信息,CDMA系统的码片之间互相具有准正交特性,以此来区分各路原始信号,各路信号在时间、频率、空间上都有可能会重叠。
同时码分复用还有一个优点可以降低信噪比,因为总的信号增加了。
图片来自《网络技术与应用MOOC》