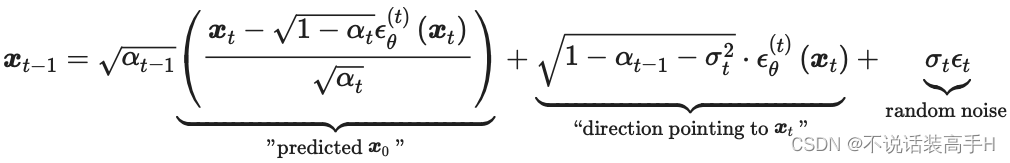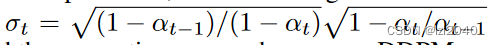在构建回归模型时，如果自变量X为连续性变量，回归系数β可以解释为：在其他自变量不变的条件下，X每改变一个单位，所引起的因变量Y的平均变化量；如果自变量X为二分类变量，例如是否饮酒（1=是，0=否），则回归系数β可以解释为：其他自变量不变的条件下，X=1（饮酒者）与X=0（不饮酒者）相比，所引起的因变量Y的平均变化量。

但是，当自变量X为多分类变量时，例如职业、学历、血型、疾病严重程度等等，此时仅用一个回归系数来解释多分类变量之间的变化关系，及其对因变量的影响，就显得太不理想。

此时，我们通常会将原始的多分类变量转化为哑变量，每个哑变量只代表某两个级别或若干个级别间的差异，通过构建回归模型，每一个哑变量都能得出一个估计的回归系数，从而使得回归的结果更易于解释，更具有实际意义。

哑变量

哑变量（Dummy Variable），又称为虚拟变量、虚设变量或名义变量，从名称上看就知道，它是人为虚设的变量，通常取值为0或1，来反映某个变量的不同属性。对于有n个分类属性的自变量，通常需要选取1个分类作为参照，因此可以产生n-1个哑变量。

将哑变量引入回归模型，虽然使模型变得较为复杂，但可以更直观地反映出该自变量的不同属性对于因变量的影响，提高了模型的精度和准确度。

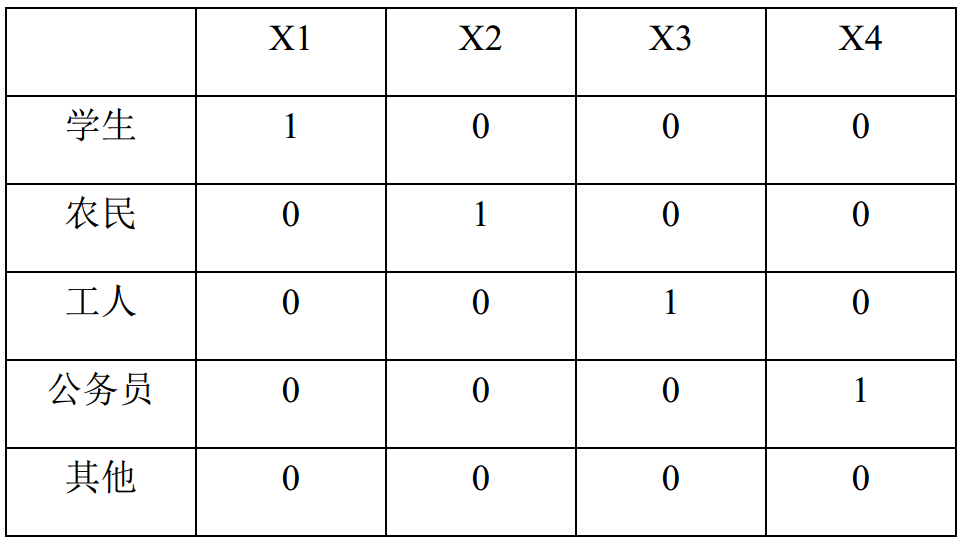
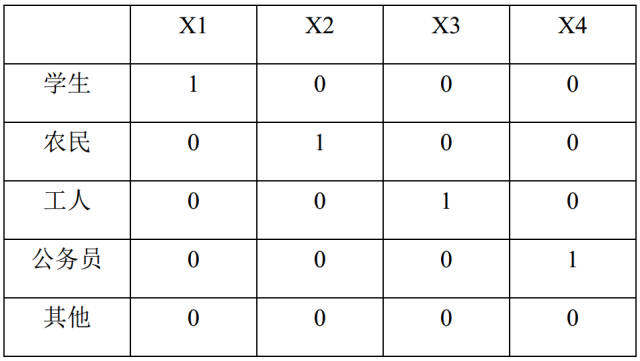
举一个例子，如职业因素，假设分为学生、农民、工人、公务员、其他共5个分类，其中以“其他职业”作为参照，此时需要设定4哑变量X1-X4，如下所示：

X1=1，学生；X1=0，非学生；

X2=1，农民；X2=0，非农民；

X3=1，工人；X3=0，非工人；

X4=1，公务员；X4=0，非公务员；

那么对于每一种职业分类，其赋值就可以转化为以下形式：

什么情况下需要设置哑变量

1. 对于无序多分类变量，引入模型时需要转化为哑变量

举一个例子，如血型，一般分为A、B、O、AB四个类型，为无序多分类变量，通常情况下在录入数据的时候，为了使数据量化，我们常会将其赋值为1、2、3、4。

从数字的角度来看，赋值为1、2、3、4后，它们是具有从小到大一定的顺序关系的，而实际上，四种血型之间并没有这种大小关系存在，它们之间应该是相互平等独立的关系。如果按照1、2、3、4赋值并带入到回归模型中是不合理的，此时我们就需要将其转化为哑变量。

2. 对于有序多分类变量，引入模型时需要酌情考虑

例如疾病的严重程度，一般分为轻、中、重度，可认为是有序多分类变量，通常情况下我们也常会将其赋值为1、2、3（等距）或1、2、4（等比）等形式，通过由小到大的数字关系，来体现疾病严重程度之间一定的等级关系。

但需要注意的是，一旦赋值为上述等距或等比的数值形式，这在某种程度上是认为疾病的严重程度也呈现类似的等距或等比的关系。而事实上由于疾病在临床上的复杂性，不同的严重程度之间并非是严格的等距或等比关系，因此再赋值为上述形式就显得不太合理，此时可以将其转化为哑变量进行量化。

3. 对于连续性变量，进行变量转化时可以考虑设定为哑变量

对于连续性变量，很多人认为可以直接将其带入到回归模型中即可，但有时我们还需要结合实际的临床意义，对连续性变量作适当的转换。例如年龄，以连续性变量带入模型时，其解释为年龄每增加一岁时对于因变量的影响。但往往年龄增加一岁，其效应是很微弱的，并没有太大的实际意义。

此时，我们可以将年龄这个连续性变量进行离散化，按照10岁一个年龄段进行划分，如0-10、11-20、21-30、31-40等等，将每一组赋值为1、2、3、4，此时构建模型的回归系数就可以解释为年龄每增加10岁时对因变量的影响。

以上赋值方式是基于一个前提，即年龄与因变量之间存在着一定的线性关系。但有时候可能会出现以下情况，例如在年龄段较低和较高的人群中，某种疾病的死亡率较高，而在中青年人群中，死亡率却相对较低，年龄和死亡结局之间呈现一个U字型的关系，此时再将年龄段赋值为1、2、3、4就显得不太合理了。

因此，当我们无法确定自变量和因变量之间的变化关系，将连续性自变量离散化时，可以考虑进行哑变量转换。

还有一种情况，例如将BMI按照临床诊断标准分为体重过低、正常体重、超重、肥胖等几种分类时，由于不同分类之间划分的切点是不等距的，此时赋值为1、2、3就不太符合实际情况，也可以考虑将其转化为哑变量。

如何选择哑变量的参照组

在上面的内容中我们提到，对于有n个分类的自变量，需要产生n-1个哑变量，当所有n-1个哑变量取值都为0的时候，这就是该变量的第n类属性，即我们将这类属性作为参照。

例如上面提到的以职业因素为例，共分为学生、农民、工人、公务员、其他共5个分类，设定了4哑变量，其中职业因素中“其它”这个属性，每个哑变量的赋值均为0，此时我们就将“其它”这个属性作为参照，在最后进行模型解释时，所有类别哑变量的回归系数，均表示该哑变量与参照相比之后对因变量的影响。

在设定哑变量时，应该选择哪一类作为参照呢？

1. 一般情况下，可以选择有特定意义的，或者有一定顺序水平的类别作为参照

例如，婚姻状态分为未婚、已婚、离异、丧偶等情况，可以将“未婚”作为参照；或者如学历，分为小学、中学、大学、研究生等类别，存在着一定的顺序，可以将“小学”作为参照，以便于回归系数更容易解释。

2. 可以选择临床正常水平作为参照

例如，BMI按照临床诊断标准分为体重过低、正常体重、超重、肥胖等类别，此时可以选择“正常体重”作为参照，其他分类都与正常体重进行比较，更具有临床实际意义。

3. 还可以将研究者所关注的重点类别作为参照

例如血型，分为A、B、O、AB四个类型，研究者更关注O型血的人，因此可以将O型作为参照，来分析其他血型与O型相比后对于结局产生影响的差异。

下面我们将结合SPSS软件，向大家介绍在回归模型中何如实现哑变量的设置，并对引入哑变量后的模型结果进行解读。

Logistic /Cox回归

在SPSS中，Logistic回归和Cox回归设置哑变量的方式是一致的，因此本文以Logistic回归为例进行说明。

一、研究实例

某研究人员拟探讨不同种族人群中某疾病发病风险有无差异，收集了4种不同种族人群的相关数据资料（1=Black美国黑人，2=White美国白人，3=Indian美国印第安人，4=Asian亚裔美国人）。

根据数据类型判断，种族为无序多分类资料，需要将种族转化为哑变量后，进行Logistic回归。

二、SPSS操作

1. Analyze → Regression → Binary Logistic，进入到Logistic回归模块

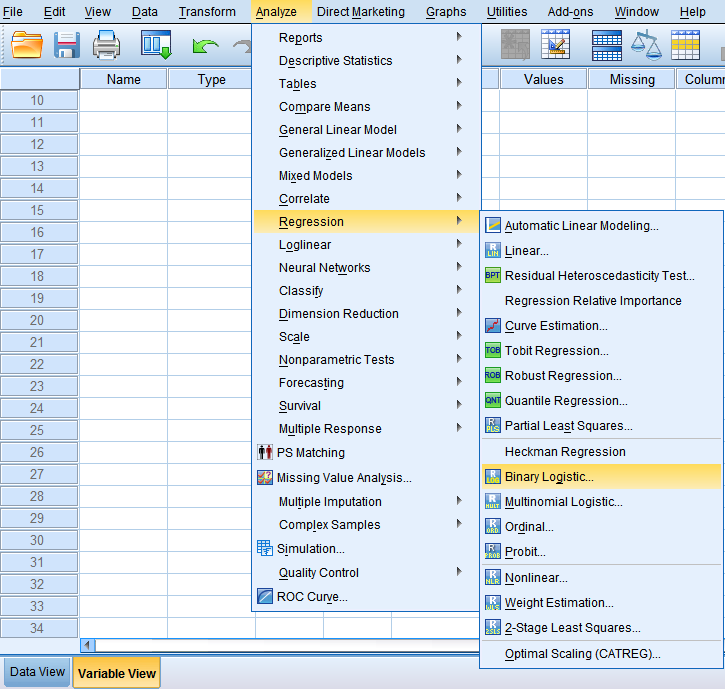
2. 将Event选入Dependent框中，将Gender、Age、Race选入Covariates框中

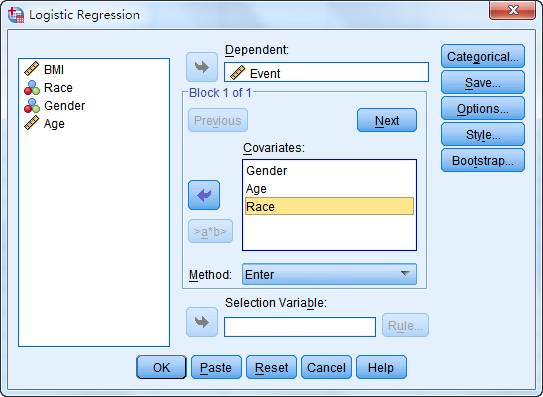
3. 点击Categorical进入定义分类变量的对话框，将需要转化的变量Race选入Categorical Covariates框中，点击Contrast旁的下拉框选择Indicator，Reference Category设置为First，即设定第一个分类为参照。

在本次研究中，Race=1为黑人，即我们选择黑人作为参照。最后再点击Change确认更改为Race（Indicator（first））。

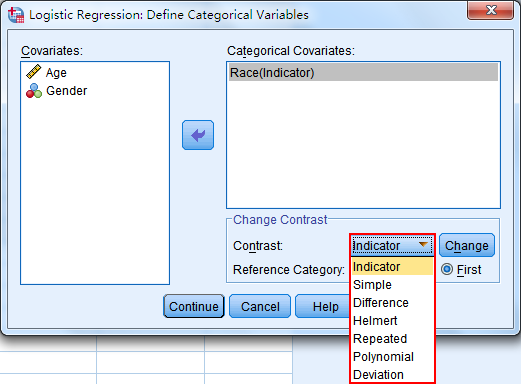
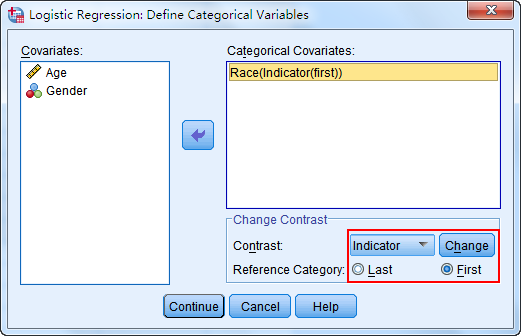
在选择哑变量编码方式时，Contrast下拉选项一共提供了7种编码方式：

(1) Indicator（指示对比）：用于指定某一分类为参照，指定的参照取决于Reference Category中选择Last还是First，即只能以该变量的第一类或者最后一类作为参照。Indicator为默认方法，也是我们最常用的设置参照类的方法。

(2) Simple（简单对比）： Simple和Indicator两个方法虽然参数编码不同，但其实质是一样的，均为各分类分别与参照进行相比。

(3) Difference（差异对比）：即该分类变量的某个分类，与前面所有分类的平均值进行比较，此法与Helmert法相反，因此也叫做反Helmert法。此选项常用于有序分类变量。

(4) Helmert（赫尔默特对比）：即该分类变量的某个分类，与其后面所有分类的平均值进行比较，同样也适用于有序分类变量。

(5) Repeated（重复对比）：即该分类变量的各个分类，均与前面相邻的一个分类进行比较，此时前一分类为参照。

(6) Polynomial（多项式对比）：它假设各个分类间隔是等距的，只能用于数值型的变量。（注意：如果此时原始变量为字符型，例如A、B、C、D，在SPSS中使用该方法时它会提示Polynomial contrasts may not be specified for string variables。而对于其他6种方法是允许原始变量是字符型，SPSS可以将其自动转化为0或1形式的哑变量。）

(7) Deviation（偏差对比）：即除参照外，其余每一个分类都与总体水平相比，此时每个分类的回归系数都是相对于总体水平而言的改变量。

4. 点击Continue回到主对话框，再点击OK完成操作。

三、结果解读

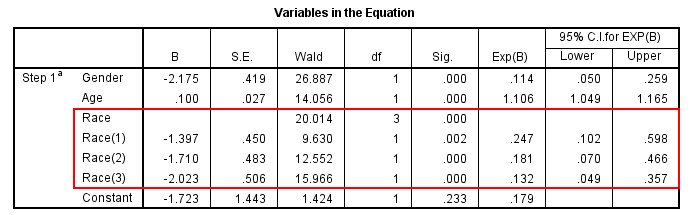
1. 结果显示， SPSS将 Race自动转化为3个哑变量，分别为Race(1) (2) (3)，代表白人、印第安人和亚裔人，参照为黑人。在α=0.05的检验水准下，Race(1) (2) (3) 回归系数检验P值均<0.05，提示白人、印第安人和亚裔种族某疾病的发生风险均与黑人种族之间存在统计学差异。

2. 白人、印第安人和亚裔相对于黑人种族，其OR值和95% CI分别为0.247(0.102, 0.598)、0.181(0.070, 0.466)、0.132(0.049, 0.357)，提示白人、印第安人和亚裔人中该疾病的发生风险均显著低于黑人种族。

多重线性回归

针对多重线性回归，SPSS并没有直接的选项来帮助我们设置哑变量，我们需要通过重新编码的方式，手动将其转换为哑变量。

一、研究实例

仍然以上面的研究实例进行介绍，某研究人员拟探讨不同种族人群中BMI有无差异，收集了4种不同种族人群的相关数据资料（1=Black美国黑人，2=White美国白人，3=Indian美国印第安人，4=Asian亚裔美国人）。

根据数据类型判断，种族为无序多分类资料，需要将种族转化为哑变量后，进行多重线性回归。

二、SPSS操作

1. Transform → Recode into Different Variables

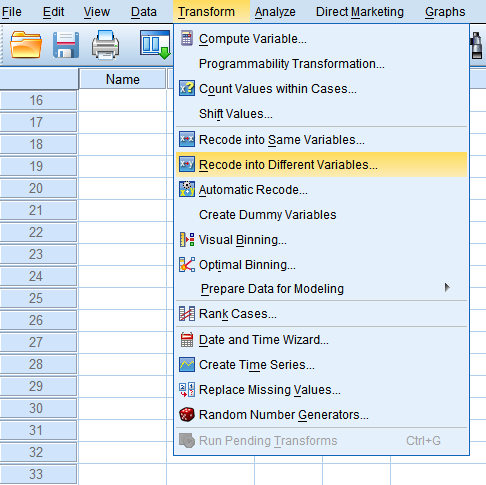
将需要转换为哑变量的Race因素选入Numeric Variable->Output Variable框中，在Name框中输入转变的第一个哑变量名字Race1，并点击Change进行命名

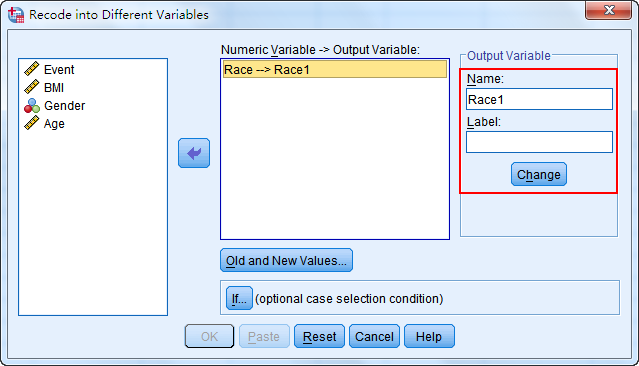
2. 点击Old and New Values进入重新编码的对话框

在Old Value中的Value框中填写1，在New Value中的Value框中填写1，并点击Add添加，得到1->1。

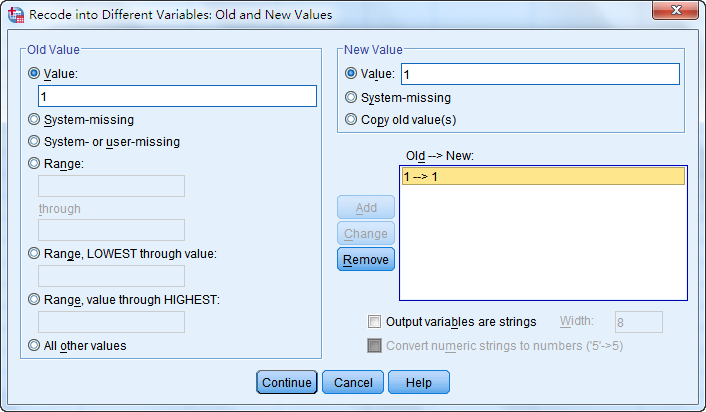
然后选择Old Value中的All other values，在New Value中的Value框中填写0，并点击Add添加，得到ELSE->0

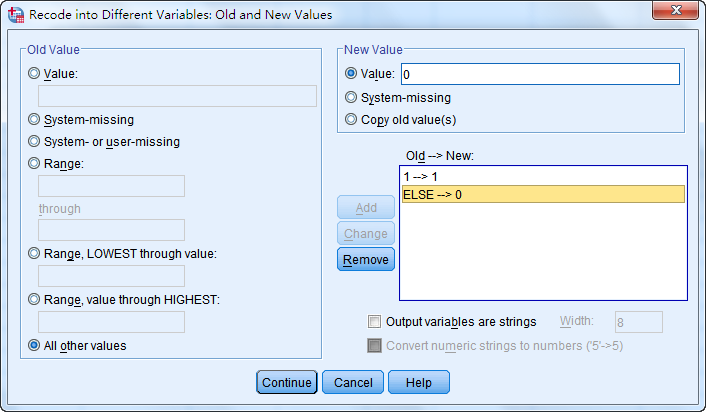
上述步骤表示将原有变量Race中第1分类，在哑变量Race1中赋值为1，将其他所有分类在哑变量Race1中赋值为0。

按照同样的方法，我们可以生成Race2和Race3，共3个哑变量。如果觉得生成3个哑变量很麻烦，我们可以进入程序编辑页面，编写一条简单的程序进行重新编码赋值，如下图所示。

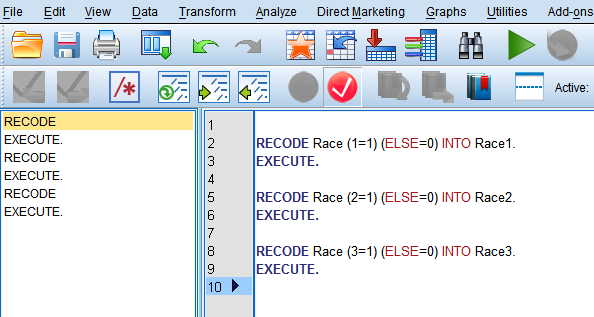
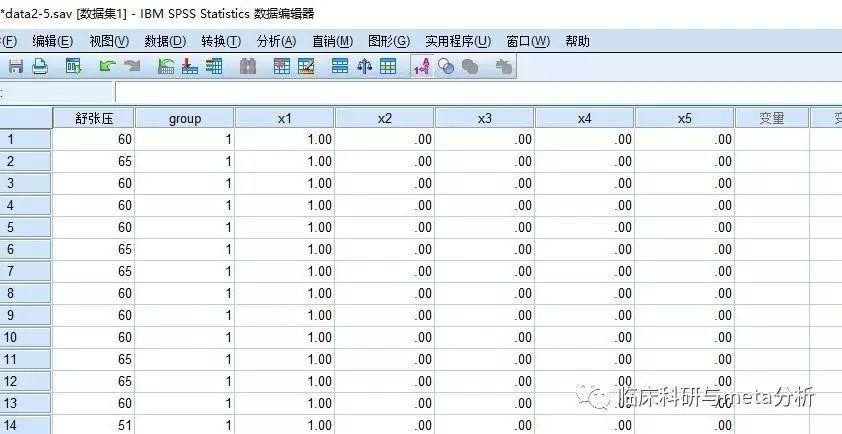
赋值完成后，我们就可以在数据视图界面看到新生成的3个哑变量。哑变量生成好后，我们就可以开始进行多重线性回归了。

3. Analyze → Regression → Linear

将BMI选入Dependent框中，将Race1、Race2、Race3、Gender和Age一同选入Independent（s）框中，Method选择Enter法，点击OK完成操作。

三、结果解读

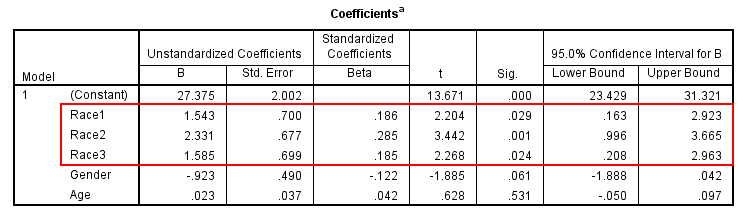
1. 我们通过重新编码将Race转化为3个哑变量，分别为Race1、2、3，代表黑人、白人和印第安人，此时参照为亚裔人。在α=0.05的检验水准下，Race1、2、3回归系数检验P值均<0.05，提示黑人、白人和印第安人的BMI均与亚裔人之间存在统计学差异。

2. 黑人、白人和印第安人与亚裔人相比，其β值和95% CI分别为1.543(0.163, 2.923)、2.331(0.996, 3.665)、1.585(0.208, 2.963)，提示黑人、白人和印第安人的BMI要显著高于亚裔人。

设置哑变量时的注意事项

1. 原则上哑变量在模型中应同进同出，也就是说在一个模型中，如果同一个分类变量的不同哑变量，出现了有些哑变量有统计学显著性，有些无统计学显著性的情况下，为了保证所有哑变量代表含义的正确性，应当在模型中纳入所有的哑变量。

因此，我们在引入哑变量进入模型时，需选择Enter强制进入法，以保证所有哑变量都能保留在最后的模型中。

2. 上一期内容中我们介绍了如何选择参照，但需要注意的是，被选为参照的那一类分组，应该保证有一定的样本量。如果参照组样本量太少，则将会导致其他分类与参照相比时，参数估计的标准误较大，可信区间较大，精度降低，会出现估计参数极大或极小的现象。