哑变量与逻辑回归

数据

部分数据：

admit,gre,gpa,rank
0,380,3.61,3
1,660,3.67,3
1,800,4,1
1,640,3.19,4
0,520,2.93,4
1,760,3,2
1,560,2.98,1
0,400,3.08,2
1,540,3.39,3
0,700,3.92,2
0,800,4,4
0,440,3.22,1
1,760,4,1
0,700,3.08,2
1,700,4,1

导入库

• numpy: Python的语言扩展，定义了数字的数组和矩阵

• pandas: 直接处理和操作数据的主要package

• statsmodels: 统计和计量经济学的package，包含了用于参数评估和统计测试的实用工具

• pylab: 用于生成统计图

# 导入库
import pandas as pd
import statsmodels.api as sm
from matplotlib import pyplot as plt 
import numpy as np

读入数据
辨别不同的因素对研究生录取的影响。

数据集中的前三列可作为预测变量(predictorvariables)：gpa/gre分数/rank表示本科生母校的声望。第四列admit则是二分类目标变量(binary targetvariable)，它表明考生最终是否被录用。

#读入数据：
df = pd.read_csv('../测试数据/python/binary.csv')

打印前5行

# 打印前5行
df.head()

输出：

admit	gre	gpa	rank
0	0	380	3.61	3
1	1	660	3.67	3
2	1	800	4.00	1
3	1	640	3.19	4
4	0	520	2.93	4

重命名字段

# rank重命名为prestige
df.columns = ['admit', 'gre', 'gpa', 'prestige']
df.columns

输出：

Index(['admit', 'gre', 'gpa', 'prestige'], dtype='object')

查看统计信息

我们可以使用pandas的函数describe来给出数据的摘要

# 统计摘要以及查看数据
print('统计摘要:')
df.describe()

输出：

admit		gre			gpa			prestige
count	400.000000	400.000000	400.000000	400.00000
mean	0.317500	587.700000	3.389900	2.48500
std	0.466087	115.516536	0.380567	0.94446
min	0.000000	220.000000	2.260000	1.00000
25%	0.000000	520.000000	3.130000	2.00000
50%	0.000000	580.000000	3.395000	2.00000
75%	1.000000	660.000000	3.670000	3.00000
max	1.000000	800.000000	4.000000	4.00000

查看每一列的标准差

# 查看每一列的标准差
print('标准差:')
df.std()

输出：

admit         0.466087
gre         115.516536
gpa           0.380567
prestige      0.944460
dtype: float64

频率表，表示prestinge与admin的值相应的数量关系

pd.crosstab(df['admit'], df['prestige'], rownames=['admit'])

输出：

prestige	1	2	3	4
admit				0	28	97	93	551	33	54	28	12

创建哑变量（虚拟变量）

虚拟变量，也叫哑变量，可用来表示分类变量、非数量因素可能产生的影响。在计量经济学模型，需要经常考虑属性因素的影响。例如，职业、文化程度、季节等属性因素往往很难直接度量它们的大小。只能给出它们的“Yes—D=1”或”No—D=0”，或者它们的程度或等级。为了反映属性因素和提高模型的精度，必须将属性因素“量化”。通过构造0-1型的人工变量来量化属性因素。

pandas提供了一系列分类变量的控制。我们可以用get_dummies来将”prestige”一列虚拟化。

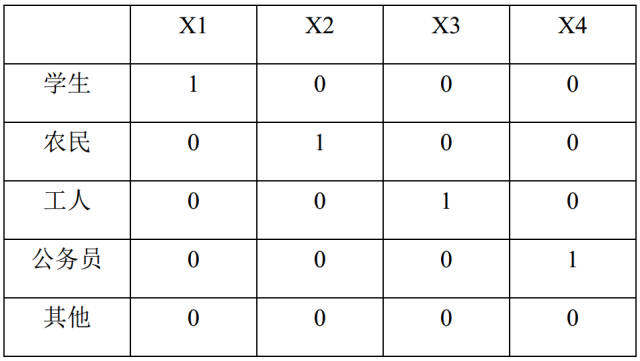
get_dummies为每个指定的列创建了新的带二分类预测变量的DataFrame，在本例中，prestige有四个级别：1，2，3以及4（1代表最有声望），prestige作为分类变量更加合适。当调用get_dummies时，会产生四列的dataframe，每一列表示四个级别中的一个。

这样，数据原本的prestige属性就被prestige_x代替了，例如原本的数值为2，则prestige_2为1，prestige_1、prestige_3、prestige_4都为0。

将新的虚拟变量加入到了原始的数据集中后，就不再需要原来的prestige列了。在此要强调一点，生成m个虚拟变量后，只要引入m-1个虚拟变量到数据集中，未引入的一个是作为基准对比的。

最后，还需加上常数intercept，statemodels实现的逻辑回归需要显式指定。

dummy_ranks = pd.get_dummies(df['prestige'], prefix='prestige')
dummy_ranks.head()

输出：

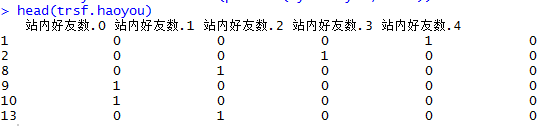
prestige_1	prestige_2	prestige_3	prestige_4
0	0			0			1			0
1	0			0			1			0
2	1			0			0			0
3	0			0			0			1
4	0			0			0			1

创建逻辑回归所需的dataframe

除admit、gre、gpa外，加入了上面常见的虚拟变量

注意，引入的虚拟变量列数应为虚拟变量总列数减1，减去的1列作为基准

cols_to_keep = ['admit', 'gre', 'gpa']
data = df[cols_to_keep].join(dummy_ranks.loc[ : , 'prestige_2':])
data.head()

输出：

	admit	gre	gpa	prestige_2	prestige_3	prestige_4
0	0		380	3.61	0	1	0
1	1		660	3.67	0	1	0
2	1		800	4.00	0	0	0
3	1		640	3.19	0	0	1
4	0		520	2.93	0	0	1

添加逻辑回归所需的intercept变量

# 需要自行添加逻辑回归所需的intercept变量
# 最后，还需加上常数intercept，statemodels实现的逻辑回归需要显式指定。
data['intercept'] = 1.0
data.head()

输出;

admit	gre	gpa	prestige_2	prestige_3	prestige_4	intercept
0	0		380	3.61	0	1	0	1.0
1	1		660	3.67	0	1	0	1.0
2	1		800	4.00	0	0	0	1.0
3	1		640	3.19	0	0	1	1.0
4	0		520	2.93	0	0	1	1.0

执行逻辑回归

实际上完成逻辑回归是相当简单的，首先指定要预测变量的列，接着指定模型用于做预测的列，剩下的就由算法包去完成了。

本例中要预测的是admin列，使用到gre、gpa和虚拟变量prestige_2、prestige_3、prestige_4。

prestige_1作为基准，所以排除掉，以防止多元共线性(multicollinearity)和引入分类变量的所有虚拟变量值所导致的陷阱(dummy variable trap)。

# 执行逻辑回归
# 指定作为训练变量的列，不含目标列‘admit’
train_clos = data.columns[1:]
logit = sm.Logit(data['admit'], data[train_clos])

拟合模型

# 拟合模型
result = logit.fit()

输出：

Optimization terminated successfully.Current function value: 0.573147Iterations 6

构建训练集并进行预测

# 构建预测集
# 与训练集相似，一般也是通过pd.read_csv()读入
# 在这里为方便，将训练集拷贝一份作为预测集
import copy
combos = copy.deepcopy(data)print(data.head())# 数据中的列要跟预测时用到的列一致
predict_cols = combos.columns[1:]# 预测集也添加intercept变量
combos['intercept'] = 1.0# 进行预测，并将预测评分存入predict列中
combos['predict'] = result.predict(combos[predict_cols])
print(combos.head())

输出结果：

admit  gre   gpa  prestige_2  prestige_3  prestige_4  intercept
0      0  380  3.61           0           1           0        1.0
1      1  660  3.67           0           1           0        1.0
2      1  800  4.00           0           0           0        1.0
3      1  640  3.19           0           0           1        1.0
4      0  520  2.93           0           0           1        1.0admit  gre   gpa  prestige_2  prestige_3  prestige_4  intercept   predict
0      0  380  3.61           0           1           0        1.0  0.172627
1      1  660  3.67           0           1           0        1.0  0.292175
2      1  800  4.00           0           0           0        1.0  0.738408
3      1  640  3.19           0           0           1        1.0  0.178385
4      0  520  2.93           0           0           1        1.0  0.118354

查看预测结果

# 预测完成后，predict 的值是介于 [0, 1] 间的概率值
# 我们可以根据需要，提取预测结果
# 例如，假定 predict > 0.5，则表示会被录取
# 在这边我们检验一下上述选取结果的精确度
total = 0
hit = 0
for value in combos.values:# 预测分数 predict, 是数据中的最后一列predict = value[-1]# 实际录取结果admit = int(value[0])# 假定预测概率大于0.5则表示预测被录取if predict > 0.5:total += 1# 表示预测命中if admit == 1:hit += 1# 输出结果
print('Total: %d, Hit: %d, Precision: %.2f' % (total, hit, 100.0 * hit / total))

输出：

Total: 49, Hit: 30, Precision: 61.22

查看结果的概要信息

对于回归结果的解读：

• 第4列为p值，标记为P>|z|，一般认为，p值小于0.05的自变量为显著的

# 查看数据的要点
# 模型系数，系数拟合的效果，总的拟合质量，一些统计度量
# combos
# print(result)
result.summary()

输出结果：

Logit Regression Results
Dep. Variable:	admit	No. Observations:	400
Model:	Logit	Df Residuals:	394
Method:	MLE	Df Model:	5
Date:	Tue, 14 Jul 2020	Pseudo R-squ.:	0.08292
Time:	11:11:27	Log-Likelihood:	-229.26
converged:	True	LL-Null:	-249.99
Covariance Type:	nonrobust	LLR p-value:	7.578e-08
coef	std err	z	P>|z|	[0.025	0.975]
gre	0.0023	0.001	2.070	0.038	0.000	0.004
gpa	0.8040	0.332	2.423	0.015	0.154	1.454
prestige_2	-0.6754	0.316	-2.134	0.033	-1.296	-0.055
prestige_3	-1.3402	0.345	-3.881	0.000	-2.017	-0.663
prestige_4	-1.5515	0.418	-3.713	0.000	-2.370	-0.733
intercept	-3.9900	1.140	-3.500	0.000	-6.224	-1.756

查看每个系数的置信区间

result.conf_int()

输出结果：

0	1
gre	0.000120	0.004409
gpa	0.153684	1.454391
prestige_2	-1.295751	-0.055135
prestige_3	-2.016992	-0.663416
prestige_4	-2.370399	-0.732529
intercept	-6.224242	-1.755716

查看相对危险度 odds ratio（OR）

使用每个变量系数的指数来生成odds ratio，可知变量每单位的增加、减少对录取几率的影响。

例如，如果学校的声望为2，则我们可以期待被录取的几率减少大概50%。UCLA上有一个对oddsratio更为深入的解释:在逻辑回归中如何解释oddsratios?。

np.exp(result.params)

输出：

gre           1.002267
gpa           2.234545
prestige_2    0.508931
prestige_3    0.261792
prestige_4    0.211938
intercept     0.018500
dtype: float64

使用置信区间来计算系数的影响

# 使用置信区间来计算系数的影响，来更好地估计一个变量影响录取率的不确定性
# odds ratios and 95% CI
params = result.params
conf = result.conf_int()
conf['OR'] = params
conf.columns = ['2.5%', '97.5%', 'OR']
np.exp(conf)

输出;

	2.5%	97.5%	OR
gre	1.000120	1.004418	1.002267
gpa	1.166122	4.281877	2.234545
prestige_2	0.273692	0.946358	0.508931
prestige_3	0.133055	0.515089	0.261792
prestige_4	0.093443	0.480692	0.211938
intercept	0.001981	0.172783	0.018500

评估分类器的效果

为了评估我们分类器的效果，我们将使用每个输入值的逻辑组合（logical combination）来重新创建数据集，如此可以得知在不同的变量下预测录取可能性的增加、减少。

首先我们使用名为 cartesian 的辅助函数来生成组合值

我们使用 np.linspace 创建 “gre” 和 “gpa” 值的一个范围，即从指定的最大、最小值来创建一个线性间隔的值的范围。在本例子中，取已知的最大、最小值。

# 根据最大、最小值生成 GRE、GPA 均匀分布的10个值，而不是生成所有可能的值
gres = np.linspace(data['gre'].min(), data['gre'].max(), 10)
print(gres)

输出：

[220.         284.44444444 348.88888889 413.33333333 477.77777778542.22222222 606.66666667 671.11111111 735.55555556 800.        ]

gpas = np.linspace(data['gpa'].min(), data['gpa'].max(), 10)
print(gpas)

输出：

[2.26       2.45333333 2.64666667 2.84       3.03333333 3.226666673.42       3.61333333 3.80666667 4.        ]

# 枚举所有的可能性
from sklearn.utils.extmath import cartesian
combos = pd.DataFrame(cartesian([gres, gpas, [1, 2, 3, 4], [1.]]))# 重新创建哑变量
combos.columns = ['gre', 'gpa', 'prestige', 'intercept']
dummy_ranks = pd.get_dummies(combos['prestige'], prefix='prestige')
dummy_ranks.columns = ['prestige_1', 'prestige_2', 'prestige_3', 'prestige_4']# 只保留用于预测的列
cols_to_keep = ['gre', 'gpa', 'prestige', 'intercept']
combos = combos[cols_to_keep].join(dummy_ranks.loc[:, 'prestige_2':])
combos.columns

输出：

Index(['gre', 'gpa', 'prestige', 'intercept', 'prestige_2', 'prestige_3','prestige_4'],dtype='object')

# 使用枚举的数据集来做预测
# predict_cols = combos.columns[1:]
# combos['admit_pred'] = result.predict(train_clos)
combos['admit_pred'] = result.predict(combos[train_clos])
combos.head()

输出：

gre	gpa	prestige	intercept	prestige_2	prestige_3	prestige_4	admit_pred
0	220.0	2.260000	1.0	1.0	0	0	0	0.157801
1	220.0	2.260000	2.0	1.0	1	0	0	0.087056
2	220.0	2.260000	3.0	1.0	0	1	0	0.046758
3	220.0	2.260000	4.0	1.0	0	0	1	0.038194
4	220.0	2.453333	1.0	1.0	0	0	0	0.179574

可视化预测结果

def isolate_and_plot(variable):# isolate gre and class rankgrouped = pd.pivot_table(combos, values=['admit_pred'], index=[variable, 'prestige'],aggfunc=np.mean)print(grouped.head())# in case you're curious as to what this looks like# print grouped.head()#                                 admit_pred# gre              prestige            # 220.000000 1               0.282462#                     2               0.169987#                     3               0.096544#                     4               0.079859# 284.444444 1               0.311718# make a plotcolors = 'rbgyrbgy'for col in combos.prestige.unique():plt_data = grouped.loc[grouped.index.get_level_values(1)==col]plt.plot(plt_data.index.get_level_values(0), plt_data['admit_pred'],color=colors[int(col)])plt.xlabel(variable)plt.ylabel("P(admit=1)")plt.legend(['1', '2', '3', '4'], loc='upper left', title='Prestige')plt.title("Prob(admit=1) isolating " + variable + " and presitge")plt.show()isolate_and_plot('gre')

输出：

isolate_and_plot('gpa')

输出：