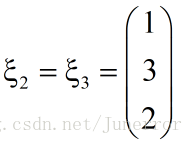矩阵特征值
设 A 是n阶方阵，如果存在数m和非零n维 列向量 x，使得 Ax=mx 成立，则称 m 是矩阵A的一个特征值（characteristic value)或 本征值（eigenvalue)。
- 矩阵特征值方法
对于矩阵A，由AX=λ 0X，λ 0EX=AX，得[λ 0E-A]X=θ即齐次线性方程组
有非零解的充分必要条件是：
即说明特征根是特征多项式|λ 0E-A| =0的根，由代数基本定理
有n个复根λ 1,λ 2,…,λ n，为A的n个特征根。当特征根λ i(I=1,2,…,n)求出后，(λ iE-A)X=θ是齐次方程，λ i均会使|λ iE-A|=0，(λ iE-A)X=θ必存在非零解，且有无穷个解向量，(λ iE-A)X=θ的基础解系以及基础解系的线性组合都是A的特征向量。
矩阵特征值示例
求矩阵 
的特征值与特征向量。
解：由特征方程
解得A有2重特征值λ 1=λ 2=-2，有单特征值λ 3=4。
对于特征值λ 1=λ 2=-2，解方程组(-2E-A)x=θ
得同解方程组x 1-x 2+x 3=0，解为x 1=x 2-x 3(x 2,x 3为自由未知量)。分别令自由未知量
得基础解系
所以A的对应于特征值λ 1=λ 2=-2的全部特征向量为x=k 1ξ 1+k 2ξ 2(k 1,k 2不全为零)，可见，特征值λ=-2的特征向量空间是二维的。注意，特征值在重根时，特征向量空间的维数是特征根的 重数。
对于特征值λ 3=4，方程组(4E-A)x=q
得同解方程组为
通解为
令自由未知量x 3=2得基础解系ξ 3 
，所以A的对于特征值λ 3=4得全部特征向量为x= k 3ξ 3。 [1]
