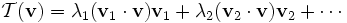如何理解矩阵特征值的意义?
毕业多年,曾经有同事问我该如何理解特征值的意义?
当时,实在羞愧,我一学数学的,真不知该如何回答。
极力回想,也只能以“特征值的求法、步骤…bla…bla…”应付了事,
答非所问,简直了得!
这样的答案教科书里写得清清楚楚,网上Google/百度一大堆,
人家问的是意义,如何理解其意义?
直扣灵魂,
我真的曾经理解过它的意义吗???
招了吧,真没有!
原在数学系时,教室里,对着黑板一堆密密麻麻的公式,我也是时常神游天外的主…
考试前,为了避免挂科才熬夜突击,对着书本一一比划,至少要演算两到三张稿纸,才能勉强记住方法、步骤,哪还管得着它的意义?
这种突击式的训练记忆,忘得也快,就像写代码一样,过一阵就忘了!
课堂上,老师大多是照本宣科。
当年,
也许是自己知识阅历不够,很难理解其意义,
也许是努力不够,被足球耽误了。
也许是天赋所致,不能顿悟!
…
总之,确定那时我肯定是没有理解它的意义的。
不知道现在有多少学生还是一样?
在学习一些抽象的数学工具时,代换三、四步之后就不知所云了,往往只能靠记忆强撑,而这种记忆最多维持一周,年轻时可能长点,后来,说忘就忘了…。
有极少数天才,能在抽象世界里面一直转,抽啊抽,一直抽…并最终以此为业。
而大多数人(99+%),一到毕业,就尴尬,因为真的不理解其意义,
看似学了一些高深的数学知识,只会做题,不会运用,根本不理解公式指代符号的现实映射!进而职场上,其它方面训练缺失的短板逐渐显现后,囧是必然!
我想,这不单是数学教育的问题,也是其它各方面可能会尴尬的本源:
不理解意义!
好,扯远了,回到正题,来看灵魂之问:
如何理解特征值的意义?
最近才有些感悟,和大家分享一下。
说到特征值 λ \lambda λ,数学上,基本上是指矩阵的特征值。
说到矩阵,高等代数几乎一整本书都在讲它,最著名的数学软件叫Matlab,直译为矩阵实验室,足见其高深、复杂!
而这么复杂混乱的东西确有一个特征值, 难道不奇怪?
再说,矩阵到底有多复杂混乱?看数学公式体会一下吧:
这是一堆数,每一个数字都可以在实数域内取值(正、负、零), m 或 n m或n m或n可以无限的延伸,联想到现在的大数据,还有什么东西不能由它表示呢?如果您相信万物皆数,这儿都可以说万物皆矩阵了,万物,能不复杂?
另外,这一堆数既可以表示数据记录,还可以表示某种不知名的抽象运算(物理上叫算子),这样的数学运算,对某些对象集,确仅仅以固有的方式伸缩,且不管它是数据记录还是抽象运算,全都一样!
如此混乱复杂! 确有本征!
这不神奇吗?
数学就是这样,抽象、高级、有理!
如果这样说感觉虚玄,那么先来看一下它精确(枯燥)的数学定义:
特征值 λ \lambda λ
设 A A A是一 n × n n \times n n×n矩阵, ξ \xi ξ是一 n n n维非零列向量,若存在一数 λ \lambda λ,使得
A ξ = λ ξ A\xi=\lambda\xi Aξ=λξ
则称 λ \lambda λ为 A A A的一个特征值, ξ \xi ξ为 A A A的属于特征值 λ \lambda λ的一个特征向量。
展开 A ξ = λ ξ A\xi=\lambda\xi Aξ=λξ,
即
[ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n . . . . . . . . . . . . a n 1 a n 2 . . . a n n ] [ x 1 x 2 . . . x n ] = λ [ x 1 x 2 . .