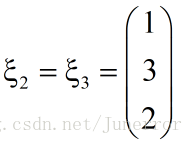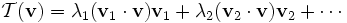【机器学习中的数学基础】矩阵特征值、特征向量和特征值分解的几何意义

在《机器学习》西瓜书中的第十章提到了“多维缩放”（简称MDS）方法，该方法是一种经典的的降维方法。此方法的目标是获得样本在$d^{{}^{\prime }}$维空间的表示，且任意两个样本在$d^{{}^{\prime }}$维空间中的欧式距离等于原始空间中的距离。

在介绍该方法时提到了特征值分解这一概念，在线性代数的课程学习中，重点放在了如何求解特征值和特征值分解，对于其表示的数学含义而不求甚解，因此，本文就矩阵的特征值、特征向量以及特征值的分解所具有的几何意义做出解释。

相关的参考：
特征向量与特征值的本质（B站）
机器学习中的数学基础：(1)实际应用中矩阵特征值与特征向量的几何意义

1、特征值和特征向量的几何意义

对于特征值和特征向量的本质不清楚的可观看上述的b站视频，实际上，

如果存在某个或某些向量在$A$作用之后，它只是伸长或者缩短，其位置仍停留在其原来张成的直线上，那么称之为$A$的特征向量，伸长或者缩短的倍数称为对应特征向量的特征值。

从几何意义上讲，特征向量描述了矩阵对应的线性变换的主要变换方向 。线性变换对向量的作用是伸缩（新的长度）和旋转（新的方向），旋转会消减拉伸的作用，特征向量只有伸缩没有旋转，它就代表了这个线性变换的主要方向；

那么特征值就是描述该方向上的变换速度（倍数），所以把特征值排序，从大到小的特征值及其特征向量能近似地描述原矩阵的主变换方向和变换速度。

2、特征值分解的几何意义

特征值分解是找最相似的矩阵：

特征值分解是将一个矩阵分解为如下形式： $A=Q\sum Q^{-1}$，
其中，$Q$是这个矩阵A的特征向量组成的矩阵，$\Sigma$是一个对角矩阵，每一个对角线元素就是一个特征值，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）。也就是说矩阵$A$的信息可以由其特征值和特征向量表示。

对于矩阵为高维的情况下，那么这个矩阵就是高维空间下的一个线性变换。可以想象，这个变换也同样有很多的变换方向，我们通过特征值分解得到的前$N$个特征向量，那么就对应了这个矩阵最主要的$N$个变化方向。我们利用这前$N$个变化方向，就可以近似这个矩阵（变换）。

3、特征值分解在图像压缩的应用

具体应用在图像压缩上，比如说，有这么一副512×512的图片（方阵才有特征值），这个图片可以放到一个矩阵里面去，就是把每个像素的颜色值填入到一个512×512512×512的 A 矩阵中。根据之前的矩阵对角化A=p，其中为对角阵，对角线上是从大到小排列的特征值，我们只保留前面50个的特征值（也就是最大的50个，其实也只占了所有特征值的百分之十），其它的都填0，重新计算矩阵后，利用新得到的矩阵，进行恢复图像，效果仍然与原图像差不多。