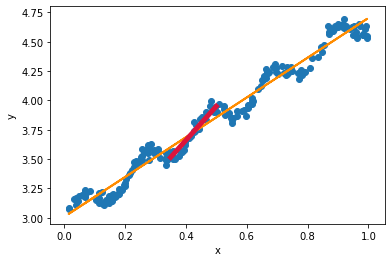
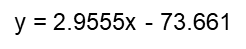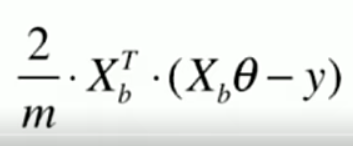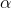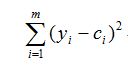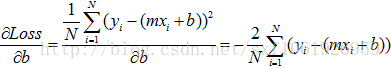一元线性回归的详细推导过程

article/2025/8/24 19:21:42

下面是一元线性回归的详细求解过程。

假设一元线性回归的最佳直线方程为：

$y = ax + b$ (1)

对于一个样本点 $x_{i}$ ，有预测值为：

$\hat{y}_{i} = ax_{i} + b$ (2)

这个样本点的真值为 $y_{i}$ ，要想获得最佳拟合方程，就需要使真值 $y_{i}$ 和预测值 $\hat{y}_{i}$ 之间的差值最小，为了后面方便求极值，使用两个值差的平方：

$\left ( y_{i} - \hat{y}_{i} \right )^{2}$ (3)

当把所有样本 $\left ( x_{1}, x_{2}, x_{3},\cdots , x_{m} \right )$ 考虑进来时，上式则为：

$\sum_{i=1}^{m}\left ( y_{i} - \hat{y}_{i} \right )^{2}$ (4)

得到上式后，现在的目标就是使上式尽可能的小，将式(2)代入上式，可得：

$\sum_{i=1}^{m}\left ( y_{i} - ax_{i}-b \right )^{2}$ (5)

此时的目标是找到a和b，使得式(5)尽可能的小，这就转化成了最优化问题：

$J\left ( a,b \right )=\sum_{i=1}^{m}\left ( y_{i} -ax_{i}-b\right )^{2} \left$ (6)

要求上式的最小值，其实就是求该式的极值，需要对上式进行求导，导数为0的位置就是极值的位置，分别对a和b求导：

$\frac{\partial J\left ( a,b \right )}{\partial a} = 0$ $\frac{\partial J\left ( a,b \right )}{\partial b} = 0$ (7)

从式(6)可以看出，括号里，a的系数是 $x_{i}$ ，b的系数是-1，明显对b求导更简单，这里先对b求导：

$\frac{\partial J\left ( a,b \right )}{\partial b}=\sum_{i=1}^{m}2\left ( y_{i}-ax_{i}-b \right )\left ( -1 \right )=0$ (8)

对式(8)化简，去掉其中的-2，得：

$\sum_{i=1}^{m}\left ( y_{i}-ax_{i}-b \right )=0$ (9)

将式(9)的括号去掉，得：

$\sum_{i=1}^{m}y_{i} -a\sum_{i=1}^{m}x_{i}-\sum_{i=1}^{m}b=0$ (10)

式(10)的第三项其实就是mb，可写为：

$\sum_{i=1}^{m}y_{i} -a\sum_{i=1}^{m}x_{i}-mb=0$ (11)

将式(11)的mb拿到一侧，得：

$mb=\sum_{i=1}^{m}y_{i} -a\sum_{i=1}^{m}x_{i}$ (12)

式(12)的等式两边同时除以m，得：

$b= \frac{\sum_{i=1}^{m}y_{i}}{m} - \frac{a\sum_{i=1}^{m}x_{i}}{m}$ (13)

式(13)，第一项中所有 $y_{i}$ 的和除以m其实就是 $y_{i}$ 的平均值，第二项中所有 $x_{i}$ 的和除以m就是 $x_{i}$ 的平均值，所以，式(13)可写为：

$b = \bar{y} - a\bar{x}$ (14)

式(14)就是b的结果，然后基于式(6)再对a进行求导：

$\frac{\partial J\left ( a,b \right )}{\partial a}=\sum_{i=1}^{m}2\left ( y_{i}-ax_{i}-b \right )\left ( -x_{i} \right )=0$ (15)

式(15)可化简为：

$\sum_{i=1}^{m}\left ( y_{i}-ax_{i}-b \right )x_{i} =0$ (16)

将b的结果代入上式，得：

$\sum_{i=1}^{m}\left ( y_{i}-ax_{i}-\bar{y}+a\bar{x} \right )x_{i} =0$ (17)

将上式的 $x_{i}$ 乘到括号里，得：

$\sum_{i=1}^{m}\left ( x_{i}y_{i}-a\left (x_{i} \right )^{2}-x_{i}\bar{y}+a\bar{x}x_{i} \right ) =0$ (18)

把上式中含有a的项放到一起，得：

$\sum_{i=1}^{m}\left ( x_{i}y_{i}-x_{i}\bar{y} \right )-a\sum_{i=1}^{m}\left ( x_{i}^{2}-\bar{x}x_{i} \right ) =0$ (19)

再把a放到等式的左边，其它部分放到等式右边，可求得a的值为：

$a = \frac{\sum_{i=1}^{m}\left ( x_{i}y_{i}-x_{i}\bar{y} \right )}{\sum_{i=1}^{m}\left ( x_{i}^{2}-\bar{x}x_{i} \right )}$ (20)

此时已经求得了a和b的值，这里对式(20)进一步处理，分子中的第二项可做如下转换：

$\sum_{i=1}^{m}x_{i}\bar{y}=\bar{y}\sum_{i=1}^{m}x_{i} = m\bar{y}\bar{x} = \bar{x}\sum_{i=1}^{m}y_{i} = \sum_{i=1}^{m}\bar{x}y_{i}$ (21)

其中， $\bar{x}$ 和 $\bar{y}$ 是常数，则

$m\bar{y}\bar{x} = \sum_{i=1}^{m}\bar{x}\bar{y}$ (22)

基于式(21)和式(22)对(20)进行变换，得下式。由式(21)可看出，式(23)分子的第三项和第四项相等，分母的第三项与第四项其实就是将分子的第三项与第四项中的y变为了x。所以，分母的第三项和第四项也是相等的。

$a = \frac{\sum_{i=1}^{m}\left ( x_{i}y_{i}-x_{i}\bar{y} - \bar{x}y_{i} + \bar{x}\bar{y} \right )}{\sum_{i=1}^{m}\left ( x_{i}^{2}-\bar{x}x_{i} - \bar{x}x_{i} +\bar{x}^{2}\right )}$ (23)

式(23)，进一步可以合并为：

$a = \frac{\sum_{i=1}^{m}\left ( x_{i}\left ( y_{i}-\bar{y} \right ) - \bar{x}\left ( y_{i}-\bar{y} \right ) \right )}{\sum_{i=1}^{m}\left ( x_{i}^{2}-2\bar{x}x_{i} +\bar{x}^{2}\right )}$ (24)

即：

$a = \frac{\sum_{i=1}^{m}\left ( x_{i}-\bar{x} \right )\left ( y_{i}-\bar{y} \right )}{\sum_{i=1}^{m}\left ( x_{i}-\bar{x} \right )^{2}}$ (25)

此时就找了使得式(5)尽可能的小a和b，即：

$a = \frac{\sum_{i=1}^{m}\left ( x_{i}-\bar{x} \right )\left ( y_{i}-\bar{y} \right )}{\sum_{i=1}^{m}\left ( x_{i}-\bar{x} \right )^{2}}$ ， $b = \bar{y} - a\bar{x}$ (26)

以上就是一元线性回归的详细求解过程，由于是一元，这里的 $\bar{x}$ 和 $\bar{y}$ 比较容易得到，a和b也容易求得。但是，对于多元线性回归的情况，系数的求解需要使用到矩阵，而更多求解其它目标函数使用的是梯度下降法。