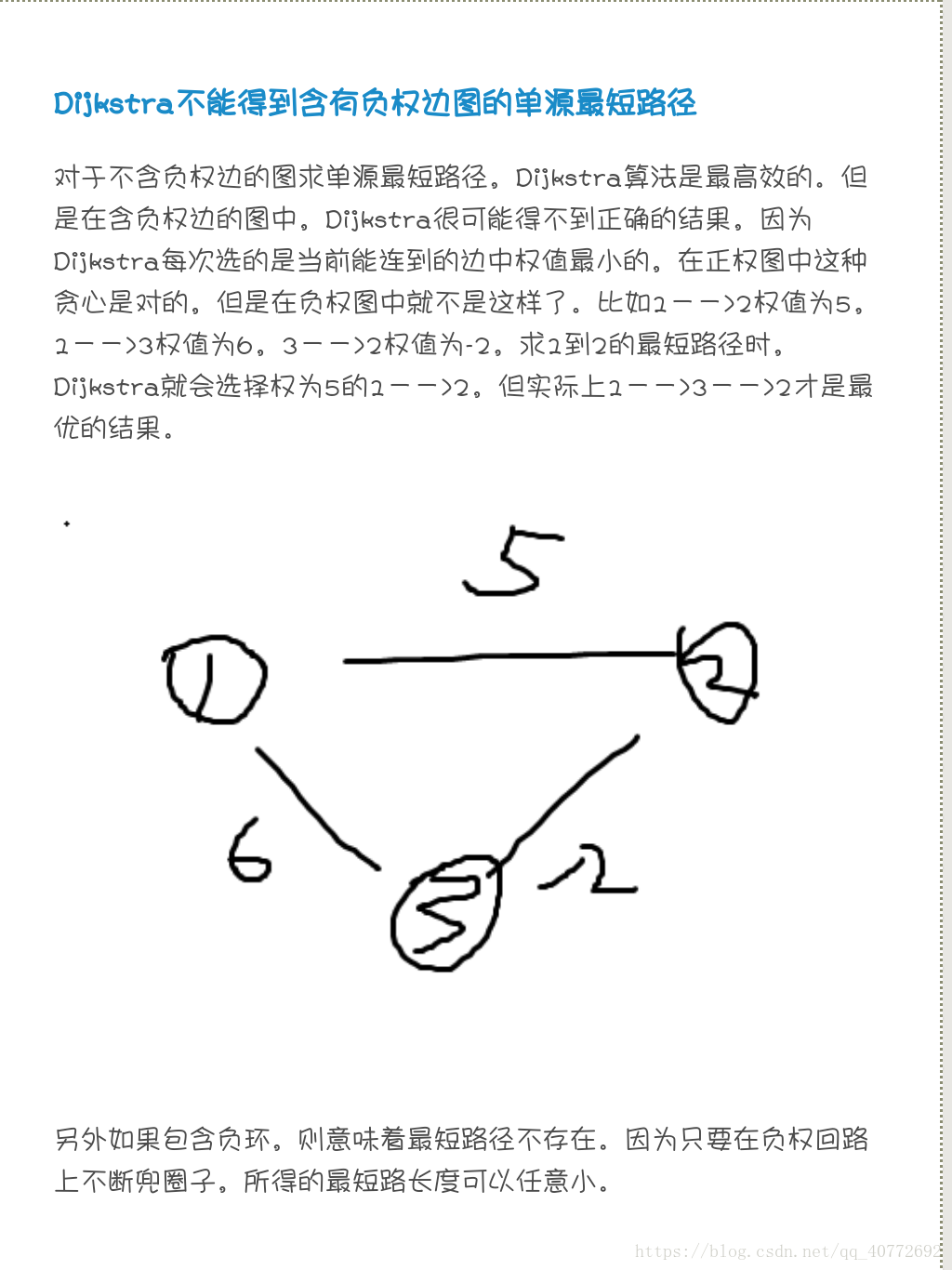
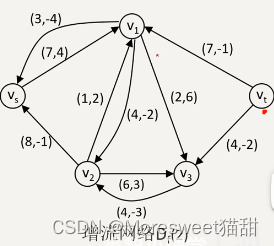
最小费用最大流算法

图片来源 《趣学算法》 人民邮电出版社 陈小玉
代码实现
/*
参考:《趣学算法》陈小玉 人民邮电出版社
最小费用最大流---最小费用路算法
问题分析:在实际应用中,要同时考虑流量和费用,每条边除了给定容量之外,还定义了一个单位流量的费用.网络流的费用=每条边的流量*单位流量费用我们希望费用最小,流量最大,因此要求解最小费用最大流容量 流量 单位流量费用(cap,flow,cost)v1--------------------->v2混合网络每个顶点有(3,2,1)v1--------------------->v2v1<---------------------v2(0,-2,-1)
算法过程:(1)先找最小费用路,在该路径上增流,称为最小费用路算法。(2)先找最大流,然后找负费用圈,消减费用,减少到最小费用,称为消圈法最小费用路算法,是在残余网络上寻找从源点到汇点的最小费用路,即从源点到汇点的以单位费用为权的最短路,然后沿着最小费用路增流,知道找不到最小费用路为止。
*/
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;const int INF=1000000;//正无穷
const int NODESIZE=100;//结点最大个数
const int EDGESIZE=10000;//最大边数
int top;//当前边下标
int maxflow;//最大流
bool vis[NODESIZE];//访问标记数组
int c[NODESIZE];//入队次数
int dist[NODESIZE];//dist[i]表示源点到点i最短距离:距离即这条路单位cost和
int pre[NODESIZE];//前驱数组struct Vertex{//邻接表头节点int first;//与之连接的边的序号
}V[NODESIZE];
struct Edge{//边表示int v,next;//v弧头 next指向下一条邻接边int cap,flow,cost;
}E[EDGESIZE];void init();//初始化
void add(int u,int v,int c,int cost);//更新混合网络
void add_edge(int u,int v,int c,int cost);//更新混合网络边
void printgraph(int n);//输出网络邻接表
void printflow(int n);//输出实流边
int MCMF(int s,int t,int n);//最小花费最大流
bool SPFA(int s,int t,int n);//求最小费用路int main(void){int nodeSize,edgeSize;int unode,vnode,weight,cost;cout<<"请输入 结点个数 和 边数: \n";cin>>nodeSize>>edgeSize;//初始化init();cout<<"请输入两个结点u,v,边u---v的容量weight,单位容量费用cost:\n";for(int i=1;i<=edgeSize;i++){cin>>unode>>vnode>>weight>>cost;add(unode,vnode,weight,cost);}//输出网络邻接表printgraph(nodeSize);cout<<"网络的最小费用:"<<MCMF(1,nodeSize,nodeSize)<<endl;cout<<"网络的最大流值:"<<maxflow<<endl;//输出最终网络printgraph(nodeSize);//输出实流变printflow(nodeSize);return 0;
}//初始化
void init(){memset(V,-1,sizeof(V));//初始化顶点top=0;//当前边下标maxflow=0;
}//更新混合网络
void add(int u,int v,int c,int cost){add_edge(u,v,c,cost);add_edge(v,u,0,-cost);
}//更新混合网络边
void add_edge(int u,int v,int c,int cost){// top top.v//u---------->v //构建邻接表:头插法 顺序存储法E[top].v=v;E[top].cap=c;E[top].flow=0;E[top].cost=cost;E[top].next=V[u].first;//.next记录链的结点,下一个边的下标V[u].first=top++;//顺序存储拉链
}
//输出网络邻接表
void printgraph(int n){cout<<"\n网络邻接表\n";for(int i=1;i<=n;i++){cout<<"v"<<i<<" ["<<V[i].first;for(int j=V[i].first;~j;j=E[j].next){cout<<"]--["<<E[j].v<<" "<<E[j].cap<<" "<<E[j].flow<<" "<<E[j].cost<<" "<<E[j].next<<"]\n";}cout<<"\n";}
}
//输出实流边
void printflow(int n){cout<<"实流边:\n";for(int i=1;i<=n;i++){for(int j=V[i].first;~j;j=E[j].next){if(E[j].flow>0){cout<<"v"<<i<<"--"<<"v"<<E[j].v<<" "<<E[j].flow<<" "<<E[j].cost<<"\n";}}}
}
//最小花费最大流
int MCMF(int s,int t,int n){int d;//可增量int i,mincost;mincost=0;//maxflow为网络当前最大流量,mincost为网络当前最小费用while(SPFA(s,t,n)){//有从s到t的最小费用路d=INF;//初始化增流量cout<<"增广路径: "<<t; // i i^1 i i+1 i i+1=i^1 i i-1=i^1for(i=pre[t];i!=-1;i=pre[E[i^1].v]){//i=pre[u.v] u---->v u<----v u---->v u<---v,通俗些就是u-->v就v<---u v<--u u-->vd=min(d,E[i].cap-E[i].flow);//迭代找最小可增量cout<<"--"<<E[i^1].v;}cout<<"\n";cout<<"增流量: "<<d<<"\n";//更新最大流maxflow+=d;//增广路上正向边流量+d 反向边流量-dfor(int i=pre[t];i!=-1;i=pre[E[i^1].v]){E[i].flow+=d;E[i^1].flow-=d;}mincost+=dist[t]*d;//源点到t的单位花费*新增的流量}return mincost;
}
//求最小费用路
bool SPFA(int s,int t,int n){int u,v;queue<int>qu;//队列memset(vis,false,sizeof(vis));//标记结点是否已经访问过了memset(c,0,sizeof(c));//入队次数memset(pre,-1,sizeof(pre));//前驱数组初始化为-1//距离初始化:源点到各个结点的最短距离for(int i=1;i<=n;i++){dist[i]=INF;}//源点入队vis[s]=true;c[s]++;dist[s]=0;qu.push(s);while(!qu.empty()){//取队头,并消除标记u=qu.front();qu.pop();vis[u]=false;//遍历结点u的邻接表:即遍历u的所有出度边u--->xfor(int i=V[u].first;i!=-1;i=E[i].next){v=E[i].v;//u---->vif(E[i].cap>E[i].flow && dist[v]>dist[u]+E[i].cost){//松弛操作:这条边还可以增流且借助u-->v比直接到v cost少,如果不可增流则这条边不连通//更新源点--->v costdist[v]=dist[u]+E[i].cost;//记录v的前驱,pre记录的是边-->v 通过这条边最短到v 则v的前驱为这条边的下标pre[v]=i;//检测v是否在队列内if(!vis[v]){//不在//v结点入队列c[v]++;qu.push(v);//入队vis[v]=true;if(c[v]>n){//超过入队上上限,则说明有负环return false;}}}}}//最短可增流路径cout<<"最短可增流路径数组:\n";cout<<"dist[]=>";for(int i=1;i<=n;i++){cout<<" "<<dist[i];}cout<<"\n";if(dist[t]==INF){//如果源点到汇点距离为正无穷,则不通:找不出最短可通路径return false;}return true;
}测试样例
请输入 结点个数 和 边数:
6 10
请输入两个结点u,v,边u---v的容量weight,单位容量费用cost:
1 3 4 7
1 2 3 1
2 5 4 5
2 4 6 4
2 3 1 1
3 5 3 6
3 4 5 3
4 6 7 6
5 6 3 2
5 4 3 3网络邻接表
v1 [2]--[2 3 0 1 0]
]--[3 4 0 7 -1]v2 [8]--[3 1 0 1 6]
]--[4 6 0 4 4]
]--[5 4 0 5 3]
]--[1 0 0 -1 -1]v3 [12]--[4 5 0 3 10]
]--[5 3 0 6 9]
]--[2 0 0 -1 1]
]--[1 0 0 -7 -1]v4 [19]--[5 0 0 -3 14]
]--[6 7 0 6 13]
]--[3 0 0 -3 7]
]--[2 0 0 -4 -1]v5 [18]--[4 3 0 3 16]
]--[6 3 0 2 11]
]--[3 0 0 -6 5]
]--[2 0 0 -5 -1]v6 [17]--[5 0 0 -2 15]
]--[4 0 0 -6 -1]网络的最小费用:最短可增流路径数组:
dist[]=> 0 1 2 5 6 8
增广路径: 6--5--2--1
增流量: 3
最短可增流路径数组:
dist[]=> 0 8 7 10 13 16
增广路径: 6--4--3--1
增流量: 4
最短可增流路径数组:
dist[]=> 0 1000000 1000000 1000000 1000000 1000000
88
网络的最大流值:7网络邻接表
v1 [2]--[2 3 3 1 0]
]--[3 4 4 7 -1]v2 [8]--[3 1 0 1 6]
]--[4 6 0 4 4]
]--[5 4 3 5 3]
]--[1 0 -3 -1 -1]v3 [12]--[4 5 4 3 10]
]--[5 3 0 6 9]
]--[2 0 0 -1 1]
]--[1 0 -4 -7 -1]v4 [19]--[5 0 0 -3 14]
]--[6 7 4 6 13]
]--[3 0 -4 -3 7]
]--[2 0 0 -4 -1]v5 [18]--[4 3 0 3 16]
]--[6 3 3 2 11]
]--[3 0 0 -6 5]
]--[2 0 -3 -5 -1]v6 [17]--[5 0 -3 -2 15]
]--[4 0 -4 -6 -1]实流边:
v1--v2 3 1
v1--v3 4 7
v2--v5 3 5
v3--v4 4 3
v4--v6 4 6
v5--v6 3 2