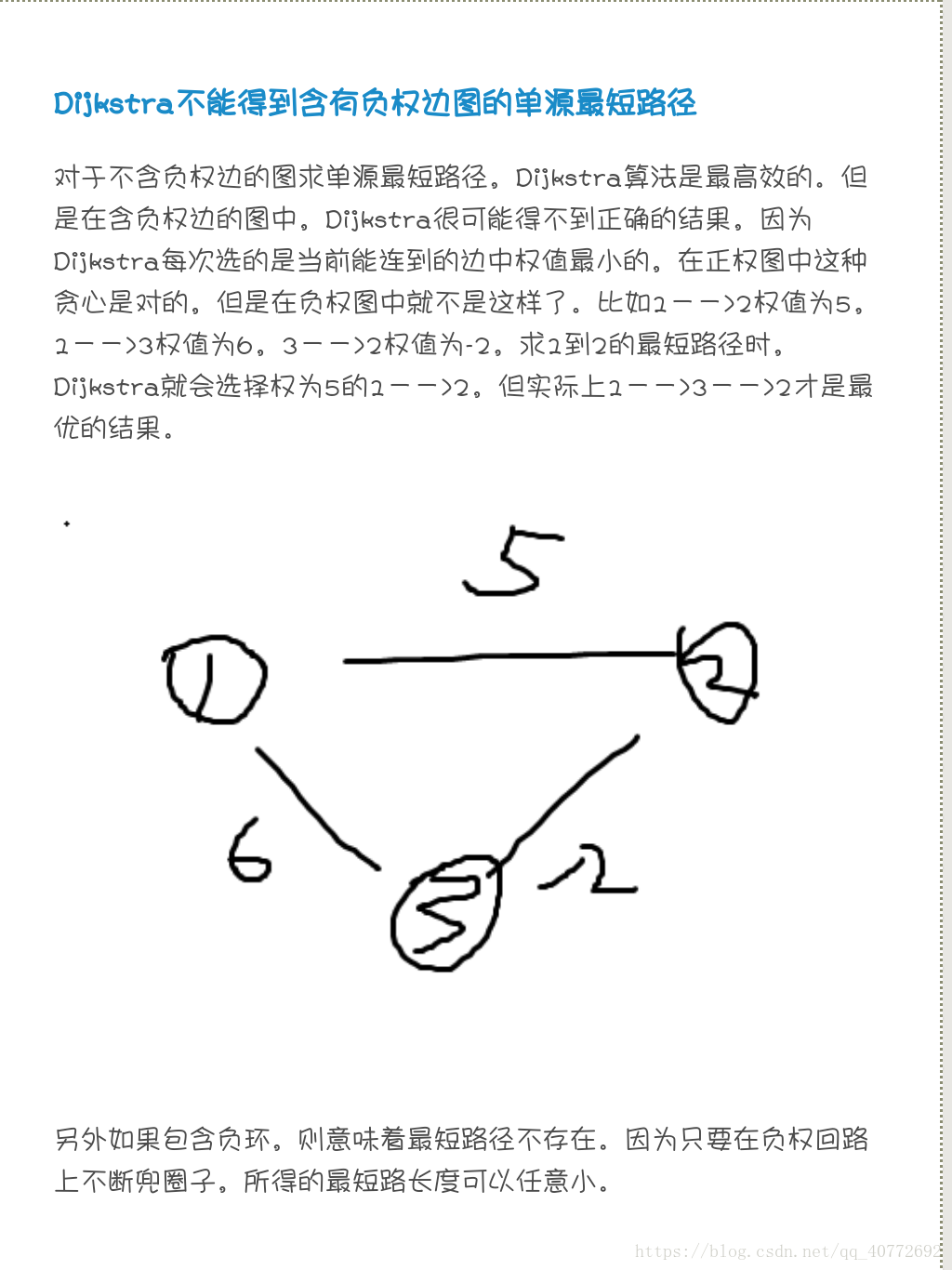
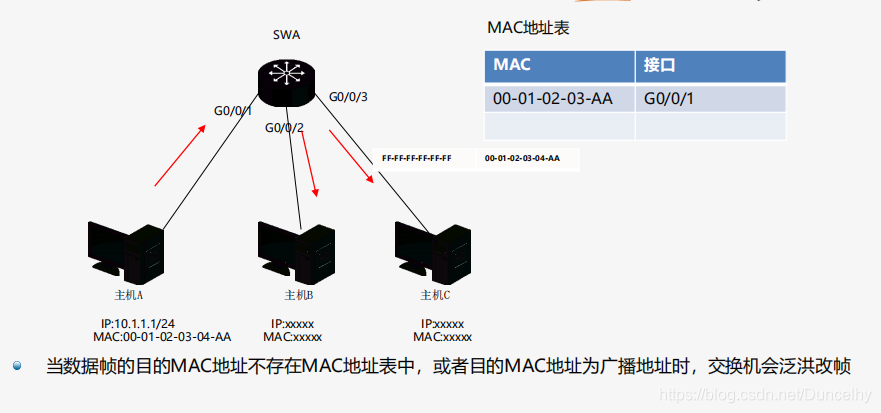
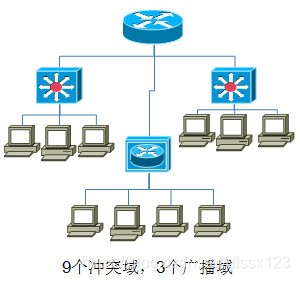
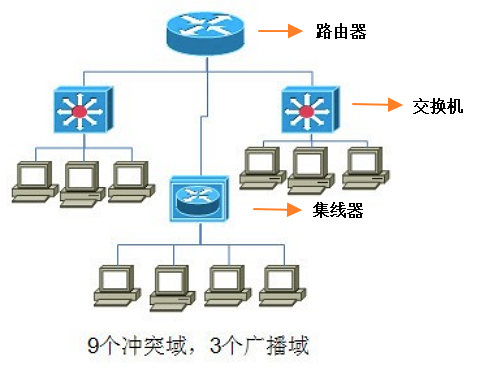
先来介绍一下什么是费用流(部分内容参考bilibili董晓算法)
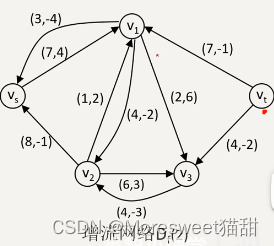
给定一个网络G=(V,E),每条边有容量限制w(u,v),还有单位流量的费用c(u,v)。
当(u,v)的流量为f(u,v)时,需要花费f(u,v)*c(u,v)的费用。
该网络中总花费最小的最大流称为最小费用最大流,总花费最大的最大流称为最大费用最大流,二者合称费用流模型,即在最大流的前提下考虑费用的最值。
一个网络的最大流是唯一的,不同路径有不同的费用。
我们用w f/c表示边的边权 流量/容量。
我们下边就主要写一些最小费用最大流的求解方法,也就是在最大流的前提下求解费用的最小值。这个过程是基于EK算法进行改进的,不懂EK算法的小伙伴可以看下这里:https://blog.csdn.net/AC__dream/article/details/126457160
我们求解最大流时是在EK算法中利用bfs找增广路,而我们现在把找增广路改成利用spfa寻找一条单位费用之和最小的增广路就可以用于在最大流的前提下求解最小费用,也就是把c(u,v)当作边权,在残留网上求最短路,这样就能够求出最小费用最大流。
为了退流,反向边的初始容量为0,反向边的容量每次+f
为了退费,反向边的初始费用为-w,走反向边的花费+f*(-c)
因为需要退费,也就是说反向边的费用是负值,那么也就是说在求解最短路的过程中存在负边权,所以要用SPFA算法。
需要注意的一点是如果图上存在单位费用的负环,那么无法直接求出该网络的最小费用最大流。此时需要先使用消圈算法消去图上的负圈。
下面附上一道模板题
题目链接:【模板】最小费用最大流 - 洛谷

样例输入:
4 5 4 3
4 2 30 2
4 3 20 3
2 3 20 1
2 1 30 9
1 3 40 5样例输出:
50 280细节见代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=5e3+10,M=1e6+10;
int h[N],ne[M],e[M],idx,pre[N];
long long w[M],c[M],d[N],mf[N];
bool vis[N];
int n,m,s,t;
void add(int x,int y,long long z1,long long z2)
{e[idx]=y;w[idx]=z1;c[idx]=z2;ne[idx]=h[x];h[x]=idx++;
}
bool spfa()
{memset(d,0x3f,sizeof d);//d[]用于求解最短路 memset(mf,0,sizeof mf);//由于函数返回值是与mf有关的,所以务必要初始化mf数组d[s]=0;mf[s]=0x3f3f3f3f3f3f3f3f; queue<int>q;q.push(s);vis[s]=true;while(!q.empty()){int x=q.front();q.pop();vis[x]=false;for(int i=h[x];i!=-1;i=ne[i]){int j=e[i];if(d[j]>d[x]+c[i]&&w[i]){mf[j]=min(mf[x],w[i]);d[j]=d[x]+c[i];pre[j]=i;if(!vis[j]){q.push(j);vis[j]=true;}}}}return mf[t]>0;
}
void EK(long long &flow,long long &cost)
{while(spfa()){int x=t;while(x!=s)//修改残留网 {int id=pre[x];w[id]-=mf[t];w[id^1]+=mf[t];x=e[id^1];}flow+=mf[t];//累加流量 cost+=mf[t]*d[t];//累加费用 }
}
int main()
{cin>>n>>m>>s>>t;for(int i=1;i<=n;i++) h[i]=-1;for(int i=1;i<=m;i++){int u,v;long long x,y;scanf("%d%d%lld%lld",&u,&v,&x,&y);add(u,v,x,y);add(v,u,0,-y);}long long flow=0,cost=0;EK(flow,cost);printf("%lld %lld",flow,cost);return 0;
}