【图论】网络流——最大流和最小费用流

1. 最大流问题

主要解决系统中的流量问题：如公路系统中的车辆流、物资调配系统中的物资流、金融系统中的现金流等。

这些问题都可以归结为网络流问题，如何安排使流量最大即最大流问题。

什么是最大流？

如左图能输送两份的水，是最大流；右图只能输送一份的水，不是最大流

1.1 基本概念

网络：图 $D=(V,A,C)$

• $V$ ：点集。其中 $v_s$ 为发点，只有发出的弧；$v_t$ 为收点，该点只有进入的弧；其余的点为中间点；
• $A$： 弧集。对于每一条弧 $(v_i,v_j)\in A$
• $C$：容量集。每一条弧的容量$c(v_i,v_j)>=0$（或简记为$c_{ij}$)，其中 C = { c i j } C=\{c_{ij}\} C={cij​}
• f = { f i j } = { f ( v i , v j ) } f=\{f_{ij}\}=\{f(v_i,v_j)\} f={fij​}={f(vi​,vj​)}：弧$(v_i,v_j)$上的流量

可行流：

(1) 容量限制条件：$0\le f_{ij}\le c_{ij}$

(2) 平衡条件：

• 中间点：流出量 = 流入量  ${\sum }_{j:\left(v_i,v_j\right)\in A}{f}_{ij}-{\sum }_{k:\left(v_k,v_i\right)\in A}{f}_{ki}=0;$
• 发点：${\sum }_{j:\left(v_s,v_j\right)\in A}{f}_{sj}=v$
• 收点：${\sum }_{k_{:}\left(v_k,v_t\right)\in A}{f}_{kt}=v$

式中：v称为这个可行流的流量,即发点的净输出量。

最大流问题可以写为如下的线性规划模型:

$$\begin{array}{l}\max v,\\ \text{ s. t. }\{\begin{array}{ll}{\sum }_{j:\left(v_s,v_j\right)\in A}{f}_{sj}=v,& \\ {\sum }_{j:(v_i,v_j)\in A}{f}_{ij}-{\sum }_{k:\left(v_k,v_i\right)\in A}{f}_{ki}=0,& i\ne s,t,\\ {\sum }_{k:\left(v_k,v_t\right)\in A}{f}_{kt}=v,& \\ 0⩽f_{ij}⩽c_{ij},& \forall \left(v_i,v_j\right)\in A.\end{array}\end{array}$$

1.2 寻求最大流的算法（Ford-Fulerson）

步骤：

1. 建立残差图, 将残差图的容量初始化

2. 当增广路径可以被找到时一直循环以下步骤：

   a. 在残差图上一直寻找增广路径
   b. 在增广路径上找到容量最小值 $x$
   c. 更新残差图上的容量：$增广路径上的容量=增广路径上的容量-x$
   d. 添加反向路径。（沿着增广路径的反方向，所有边的权重为x。）

示例：

1. 初始化： 左图为原图，右图为构建的与原图一致的残差图。

2. 第一轮循环：

① 找到如图红线的增广路径

② 可以看到整条路上容量的最大值为3，因此将路径上所有边的容量减去3

③ 去除容量为0的边，并添加值为3的反向路径

3. 第二轮循环

① 找到如图红线的增广路径

② 可以看到整条路上容量的最大值为1，因此将路径上所有边的容量减去1

③ 去除容量为0的边，并添加值为1的反向路径

④ 合并反向路径的容量值

4. 第三轮循环

① 找到如图的增广路径 （注意：这里就体现了增加的反向边的重要性了，如果没有反向边，是找不到从起点到终点的增广路径的）

② 可以看到整条路上容量的最大值为1，因此将路径上所有边的容量减去1

③ 去除容量为0的边，并添加值为1的反向路径

④ 合并反向路径的容量值

5. 第四轮循环

发现没有水流流入$v_3$，因此没有水流从起点到终点，循环终止。

6. 计算容量

$$最大流=3+1+1=5$$

代码

import copy
from collections import dequedef hasPath(Gf, s, t, path):# BFS algorithmV = len(Gf)visited = list(range(V))for i in range(V):visited[i] = Falsevisited[s] = Truequeue = deque([s])	# 起点入队while queue:temp = queue.popleft()	# 队头元素if temp == t:	# 如果到达了终点return Truefor i in range(V):	# 遍历队头元素的每个邻点# 如果零点没有被访问且流量为正向if not visited[i] and (Gf[temp][i] > 0):queue.append(i)visited[i] = Truepath[i] = temp   # 节点i的父节点为tempreturn visited[t]def max_flow(graph, s, t):maxFlow = 0Gf = copy.deepcopy(graph)V = len(Gf)path = list(range(V))# 只要有增广路径就一直循环while hasPath(Gf, s, t, path):min_flow = float('inf')# 不断利用道路上的父节点回溯，找到增广路径上的容量最小值v = twhile v != s:	u = path[v]min_flow = min(min_flow, Gf[u][v])v = path[v]print(min_flow)# 增广路径上的容量减去最小值，并添加反向路径v = twhile v != s:u = path[v]Gf[u][v] -= min_flowGf[v][u] += min_flowv = path[v]maxFlow += min_flowreturn maxFlowM=0
capacity = [
[0,16,13,M,M,M],
[M,0,10,12,M,M],
[M,4,0,M,14,M],
[M,M,9,0,M,20],
[M,M,M,7,0,4],
[M,M,M,M,M,0]
]flow = max_flow(capacity, 0, 5)
print("flow =", flow)

1.3 matlab求最大流

如图求①到⑧的最大流

a=zeros(8);a(1,[2:4])=[6,4,5];
a(2,[3,5,6])=[3,9,9];
a(3,[4:7])=[5,6,7,3];
a(4,[3,7])=[2,5];
a(5,8)=12;
a(6,[5,8])=[8,10];
a(7,[6,8])=[4,15];
G=digraph(a);
H=plot(G,'EdgeLabel',G.Edges.Weight);
[M,F]=maxflow(G,1,8);
F.Edges,highlight(H,F);

2. 最小流问题

2.1 基本概念

在许多实际问题中，往往还要考虑网络流上的费用问题。例如在运输问题中，人们总是希望在完成运输任务时，寻求一个运输费用最小的方案。

最小流问题可以写为如下的线性规划模型:

设$b_{ij}$为弧$(v_i,v_j)$上的单位费用

$$\begin{array}{l}\min {\sum }_{j:\left(v_i,v_j\right)\in A}{f}_{ij}{b}_{ij}\\ \text{ s. t. }\{\begin{array}{ll}{\sum }_{j:\left(v_s,v_j\right)\in A}{f}_{sj}=v,& \\ {\sum }_{j:(v_i,v_j)\in A}{f}_{ij}-{\sum }_{k:\left(v_k,v_i\right)\in A}{f}_{ki}=0,& i\ne s,t,\\ {\sum }_{k:\left(v_k,v_t\right)\in A}{f}_{kt}=v,& \\ 0⩽f_{ij}⩽c_{ij},& \forall \left(v_i,v_j\right)\in A.\end{array}\end{array}$$

当 $v=最大流v_{max}$时，本问题就是最小费用最大流问题；如果$v>v_{max}$，则本问题无解

2.2 求最小流的迭代算法

（1）求出从出发点到收点的最小费用流 $\mu (v_x,v_t)$。（类似求最短路）

（2）对该通路$\mu (v_x,v_t)$分配可能的最大流量 f ˉ = min ⁡ ( v i , v j ) ∈ μ ( v s , v t ) { c i j } \bar f=\min_{(v_i,v_j)\in \mu(v_s,v_t)}\{c_{ij}\} fˉ​=min(vi​,vj​)∈μ(vs​,vt​)​{cij​}，并让通路上所有边的容量对应减少$\bar{f}$。并将通路上的饱和边的单位费用改为$\infty$.

（3）作该通路$\mu (v_s,v_t)$所有边$(v_i,v_j)$的反向边$(v_j,v_i)$。令$c_{ji}=\bar{f}，b_{ji}=-b_{ij}$

（4）重复（1）~（3），直到发点到收点的全部流量等于$v$为止，或找不到增广路到$v$

2.3 matlab 求最大费用最小流

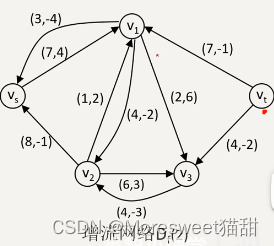
如图带有运费的网络，求从$v_s$到$v_t$的最小费用最大流，其中弧上权重的第1个数字是网络的容量，第2个数字是网络的单位运费。

NN = cellstr(strcat('v',int2str([2:5]')));  % 构造中间节点
NN = {'vs',NN{:},'vt'}; % 添加发点和收点
L ={'vs','v2',5,3;'vs','v3',3,6;'v2','v4',2,8;'v3','v2',1,2;'v3','v5',4,2;'v4','v3',1,1;'v4','v5',3,4;'v4','vt',2,10;'v5','vt',5,2};
G=digraph;G=addnode(G,NN);
G1=addedge(G,L(:,1),L(:,2),cell2mat(L(:,3)));
[M,F]=maxflow(G1,'vs','vt');    % 求最大流G2=addedge(G,L(:,1),L(:,2),cell2mat(L(:,4)));
c = full(adjacency(G1,'weighted'));
b = full(adjacency(G2,'weighted'));
f = optimvar('f',6,6,'LowerBound',0);
prob=optimproblem;
prob.Objective = sum(sum(b.*f));
con1 = [sum(f(1,:))==Msum(f(:,[2:end-1]))'==sum(f([2:end-1],:),2)sum(f(:,end))==M];
prob.Constraints.con1=con1;
prob.Constraints.con2=f<=c;
[sol,fval,flag,out ] = solve(prob);
ff=sol.f;   % 显示最小费用最大流对应的矩阵

图中对应的就是最小费用最大流：

学习对象：【13-2: Ford-Fulkerson Algorithm 寻找网络最大流】