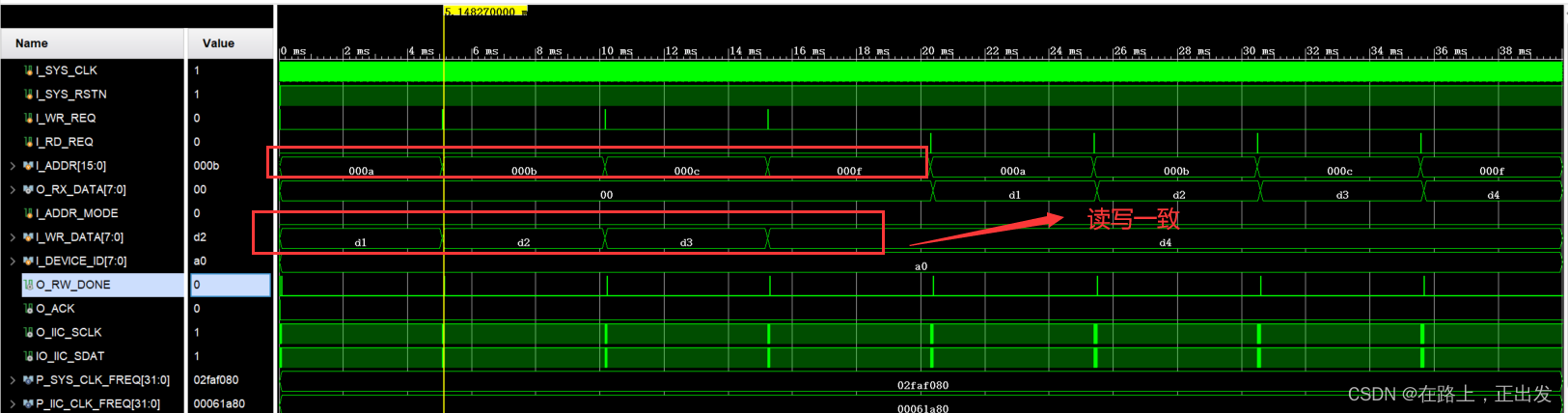
假设二叉树BT的总的结点个数为n,前序序列pre为,中序序列pin为
,现用数学归纳法证明pre和pin可以唯一确定这棵二叉树:
1. n = 1时,前序和中序序列都各只有一个元素,
,此时
等于
,为BT的根结点,唯一确定BT。
2. 假设时,pre和in可唯一确定二叉树BT,现证明当
时,命题也能得证:
时,
为二叉树的根结点,设
在pin中对应的元素为
,所以
的左子树在pin中为
,在pre中为
;
的右子树在pin中为
,在pre中为
。
若,则
没有左子树,
的右子树在pin中为
,在pre中为
。右子树结点的个数为
由假设可知,
,所以
的右子树可由pre和pin唯一确定。
若,则
没有右子树,
的左子树在pin中为
,在pre中为
。左子树结点的个数为
,由假设可知,
,所以
的左子树可由pre和pin唯一确定。
若,则
的右子树结点个数小于
,所以
的右子树可由pre和pin唯一确定;同理,
的左子树结点个数小于
,所以
的右子树可由pre和pin唯一确定。
综上所述,根结点以及
的左子树和右子树可由pre和pin唯一确定,三者唯一确定二叉树BT,命题得证。
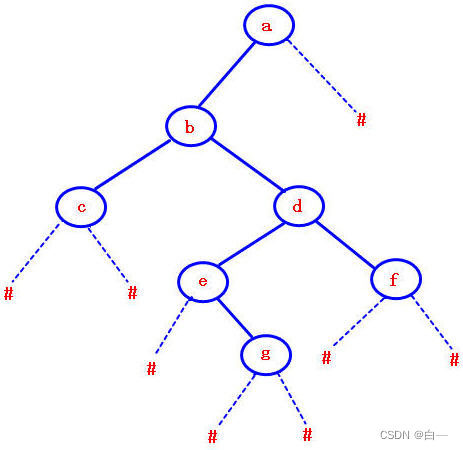
![验证二叉树的前序序列化[抽象前序遍历]](https://img-blog.csdnimg.cn/60781e71a8f34d8f86aefa8e2b77671d.png)








![IIC通信协议详解[转载]](https://img-blog.csdnimg.cn/20190210172036333.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzM4NDEwNzMw,size_16,color_FFFFFF,t_70)