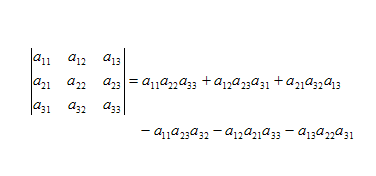一、行列式
文章目录
- 一、行列式
- 1.1 行列式性质
- 1.2 余子式
- 行列式按照行列展开的展开公式
- 一、行列式求解
- 1.用行列式
- 2.用矩阵
- 3.用特征值
- 1.3 行列式计算
- 一、具体形行列式
- (1)直接运算
- 1.行\列和相等类型
- 2.爪形、异爪形行列式
- (2)化为12+1个基本行列式
- 1. 主副对角线行列式
- 2. 拉普拉斯展开式
- 3. 范德蒙行列式
- (3)加边法
- (4)递推法
- (5)数学归纳法
- 二、抽象行列式
- 二、矩阵
- 2.1 概念
- 矩阵等价
- 2.2 矩阵运算
- 1.基本运算
- 转置矩阵
- 几种重要矩阵
- 2.矩阵乘法
- 3.向量内积和正交
- 4.施密特正交化(又称正交规范化过程)
- 2.3 矩阵的逆
- 1.逆矩阵定义
- 2.逆矩阵的性质和公式
- 3.逆矩阵的计算
- 抽象形:
- 具体形:
- 分块矩阵求逆:
- n阶对角\副对角矩阵求逆
- 2.4 伴随矩阵
- 性质和重要公式
- 2.5 初等变换和初等矩阵
- 1.行列式初等变换和矩阵初等变换的异同
- 2.初等矩阵性质
- 3.判断正交以及矩阵正交化
- 2.6 秩
- 1.定义
- 2.公式
- 3.考法
- 用阶梯型
- 2.7 矩阵相关题型
- 1. A n A^n An的题目类型
- (1) A是方阵
- (2)使用 A 2 , A 3 A^2,A^3 A2,A3推算出规律
- (3)A分解为B和C
- (4)用初等矩阵求P~1~^n^AP~2~^m^
- (5)用相似理论求A^n^(重点)
- 2.矩阵方程
- 基本化简手段
- 求解
1.1 行列式性质
- ∣ A B ∣ = ∣ A ∣ ∣ B ∣ |AB|=|A||B| ∣AB∣=∣A∣∣B∣
- 行列互换其值不变, ∣ A T ∣ = ∣ A ∣ |A^T|=|A| ∣AT∣=∣A∣
- ∣ A ∗ ∣ = ∣ A ∣ n − 1 ( 由 A A ∗ = ∣ A ∣ E 推 导 而 来 ) |A^*|=|A|^{n-1}(由AA^*=|A|E推导而来) ∣A∗∣=∣A∣n−1(由AA∗=∣A∣E推导而来)
- 行列式可拆分:某行\列元素是两个元素之和,可拆为两个行列式之和
行列式基本变换
- 行列式行或列互换,其值不变
- 行列式中某行或某列有公因子k,可以提到行列式之外
- 推论:行列式某行、列为0,行列式为0
- 行列式中某行或列的k倍加到另一行或列,行列式的值不变
- 行列式中的两行或两列对应成比例,行列式值为零
1.2 余子式
余子式和代数余子式
行列式按照行列展开的展开公式
∣ A ∣ = a i 1 A i 1 + a i 2 A i 2 + . . . + a i n A i n |A|=a_{i1}A_{i1}+a_{i2}A_{i2}+...+a_{in}A_{in} ∣A∣=ai1Ai1+ai2Ai2+...+ainAin
一、行列式求解
1.用行列式

2.用矩阵
当 ∣ A ∣ ≠ 0 |A|\neq 0 ∣A∣=0的时候,有 A ∗ = ∣ A ∣ A − 1 A*=|A|A^{-1} A∗=∣A∣A−1
由于A*是由Aij构成的,所以得出A*就可以得出所有的Aij
3.用特征值
设A为三阶可逆矩阵,其特征值分别为 λ 1 , λ 2 , λ 3 \lambda_1, \lambda_2, \lambda_3 λ1,λ2,λ3,则A-1的特征值为 λ 1 − 1 , λ 2 − 1 , λ 3 − 1 \lambda_1^{-1}, \lambda_2^{-1}, \lambda_3^{-1} λ1−1,λ2−1,λ3−1
由 A ∗ = ∣ A ∣ A − 1 A*=|A|A^{-1} A∗=∣A∣A−1可知,
λ 1 ∗ = λ 2 ⋅ λ 3 \lambda_1^*=\lambda_2\cdot \lambda_3 λ1∗=λ2⋅λ3
λ 2 ∗ = λ 1 ⋅ λ 3 \lambda_2^*=\lambda_1\cdot \lambda_3 λ2∗=λ1⋅λ3,
λ 3 ∗ = λ 1 ⋅ λ 2 \lambda_3^*=\lambda_1\cdot \lambda_2 λ3∗=λ1⋅λ2
1.3 行列式计算
一、具体形行列式
(1)直接运算
1.行\列和相等类型
行列和相等的矩阵,一般处理方法是将其他行或列依次加到第一行或列,此时第一行或列上的元素相等。
当行列和相等矩阵中的a元素位于副对角线时,应该依次对换各行或者各列。
2.爪形、异爪形行列式
- 消去其中的一条爪
- 直接计算
(2)化为12+1个基本行列式
1. 主副对角线行列式
副对角线: ( − 1 ) a ( a − 1 ) 2 a 1 , n a 2 , n − 1 a 3 , n − 2 . . . a 1 , n (-1)^{\frac{a(a-1)}{2}}a_{1,n}a_{2,n-1}a_{3,n-2}...a_{1,n} (−1)2a(a−1)a1,na2,n−1a3,n−2...a1,n
2. 拉普拉斯展开式
注意副对角拉普拉斯需要加上系数(-1)nm
TIPS:对于分块矩阵的行列式的运算,为主对角线相乘加上(-1)nm的副对角线
3. 范德蒙行列式
TIPS:
- 具体形行列式计算时,应该化出尽量多的0
- 没有0则对差别最小的元素进行处理
(3)加边法
某些一开始不适用互换、倍乘、倍加的行列式,可以考虑使用加边法:将n阶行列式添加一行和一列升至n+1阶行列式
(4)递推法
递推法主要是用于处理一般方法处理不了的异爪型行列式
递推法主要是找出Dn和Dn-1的递推关系式,实现递推,所需条件是:1.Dn比Dn-1只多一阶 2.元素分布规律相同
Tip:
- 在进行消去的时候,应该尽量使得数行或数列都为0。在进行运算时应该选择差别最小的两行进行操作。在行列和相等的题目中最常见
(5)数学归纳法

二、抽象行列式

上述的思想十分重要,将方程矩阵化是线性代数很多题目的求解核心。如果出现了多个约束方程,则可以使用方程组矩阵化
二、矩阵
2.1 概念
| ( k A ) (kA) (kA) | ( A + B ) (A+B) (A+B) | A B AB AB |
|---|---|---|
| ∣ k A ∣ = k n ∣ A ∣ |kA|=k^n|A| ∣kA∣=kn∣A∣ | ∣ A + B ∣ ≠ ∣ A ∣ + ∣ B ∣ |A+B|\neq|A|+|B| ∣A+B∣=∣A∣+∣B∣ | ∣ A B ∣ = ∣ A ∣ ∣ B ∣ = ∣ B ∣ ∣ A ∣ |AB|=|A||B|=|B||A| ∣AB∣=∣A∣∣B∣=∣B∣∣A∣ |
| ( k A T ) = k A T (kA^T)=kA^T (kAT)=kAT | ( A + B ) T = A T + B T (A+B)^T=A^T+B^T (A+B)T=AT+BT | ( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT |
| ( k A ) − 1 = 1 k A − 1 (kA)^{-1}=\frac{1}{k}A^{-1} (kA)−1=k1A−1 | ( A + B ) − 1 ≠ A − 1 + B − 1 (A+B)^{-1}\neq A^{-1}+B^{-1} (A+B)−1=A−1+B−1 | ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1 |
| ( k A ) ∗ = k n − 1 A ∗ (kA)^*=k^{n-1}A^* (kA)∗=kn−1A∗ | ( A + B ) ∗ ≠ A ∗ + B ∗ (A+B)^*\neq A^*+B^* (A+B)∗=A∗+B∗ | ( A B ) ∗ = B ∗ A ∗ (AB)^*=B^*A^* (AB)∗=B∗A∗ |
| 互换 | ||
| ( A T ) − 1 = ( A − 1 ) T (A^T)^{-1}=(A^{-1})^T (AT)−1=(A−1)T | ( A ∗ ) − 1 = ( A − 1 ) ∗ (A^*)^{-1}=(A^{-1})^* (A∗)−1=(A−1)∗ | ( A ∗ ) T = ( A T ) ∗ (A^*)^T=(A^T)^* (A∗)T=(AT)∗ |
穿脱原则:
( A B ) ∗ = B ∗ A ∗ (AB)^*=B^*A^* (AB)∗=B∗A∗, ( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT, ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
矩阵等价
如果存在矩阵A、B使得 P A Q = B PAQ =B PAQ=B,则称两个矩阵等价
性质:
反身性、传递性、等价性
|A|=k|B|
r(A)=r(B)
2.2 矩阵运算
1.基本运算
相等、加法、数乘
A是一个阶方阵,则Am=AAA…A为A的m次幂
转置矩阵
运算规律:
- ( A T ) T = A (A^T)^T=A (AT)T=A
- ( k A ) T = k A T (kA)^T=kA^T (kA)T=kAT
- ( A + B ) T = A T + B T (A+B)^T=A^T+B^T (A+B)T=AT+BT
- 如果是方阵, ∣ A T ∣ = ∣ A ∣ |A^T|=|A| ∣AT∣=∣A∣
几种重要矩阵
- 对称矩阵:AT=A的矩阵称为对称矩阵,AT=-A的矩阵称为A的反对称矩阵
- 满足ATA=E(AT=A-1)的为正交矩阵,此时A的行或列向量组是标准正交向量组
- 分块矩阵
2.矩阵乘法
- 结合律(AB)C=A(BC):比如 A T B A T B A T B = A T ( B A T B A T ) B A^TBA^TBA^TB=A^T(BA^TBA^T)B ATBATBATB=AT(BATBAT)B
- 分配律A(B+C)=AB+AC
- r ( A B ) ≤ m i n ( r ( A ) , r ( B ) ) r(AB)\leq min(r(A),r(B)) r(AB)≤min(r(A),r(B))
矩阵乘法没有交换律,也就是 A B ≠ B A AB\neq BA AB=BA
推广1:由上述可知,存在 A ≠ O A\neq O A=O并且 B ≠ O B\neq O B=O但是 A B = O AB=O AB=O的情况
推广2: ( A B ) 3 = A B A B A B ≠ A 3 B 3 (AB)^3 = ABABAB \neq A^3B^3 (AB)3=ABABAB=A3B3
推广3: A B = A C ⟹ A ( B − C ) = O AB=AC\implies A(B-C)=O AB=AC⟹A(B−C)=O, 在 A ≠ O A\neq O A=O的情况下无法推导出 B = C B=C B=C
推广4: A 2 − B 2 ≠ ( A − B ) ( A + B ) A^2-B^2 \neq (A-B)(A+B) A2−B2=(A−B)(A+B)
3.向量内积和正交
内积:向量 α \alpha α和 β \beta β的内积为 α T β = a 1 b 1 + a 2 b 2 + . . . + a n b n \alpha^T\beta=a_1b_1+a_2b_2+...+a_nb_n αTβ=a1b1+a2b2+...+anbn记作 ( α , β ) (\alpha,\beta) (α,β)
正交: α T β = 0 \alpha^T\beta=0 αTβ=0的时候,向量 α \alpha α和 β \beta β正交
模: ∣ ∣ α ∣ ∣ = a i 2 ||\alpha||=\sqrt {a_i^2} ∣∣α∣∣=ai2,若 ∣ ∣ α ∣ ∣ ||\alpha|| ∣∣α∣∣称 α \alpha α为单位向量
4.施密特正交化(又称正交规范化过程)
将线性无关向量组 α 1 , α 2 \alpha_1,\alpha_2 α1,α2的标准正交化公式为:
β 1 = α 1 \beta_1=\alpha_1 β1=α1 β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 \beta_2=\alpha_2-\frac{(\alpha_2,\beta_1)}{(\beta_1,\beta_1)}\beta_1 β2=α2−(β1,β1)(α2,β1)β1
将 β 1 , β 2 \beta_1,\beta_2 β1,β2单位化得 η 1 = β 1 ∣ ∣ β 1 ∣ ∣ \eta_1=\frac{\beta_1}{||\beta_1||} η1=∣∣β1∣∣β1, η 2 = β 2 ∣ ∣ β 2 ∣ ∣ \eta_2=\frac{\beta_2}{||\beta_2||} η2=∣∣β2∣∣β2
TIPS:
- 对于抽象向量组,需要考虑将向量组矩阵化求解
2.3 矩阵的逆
1.逆矩阵定义
定义:如果AB=BA=E,则称A是可逆矩阵,并且B是A的逆矩阵,逆矩阵是唯一的,记作A-1
A可逆的充分必要条件是 ∣ A ∣ ≠ 0 |A|\neq0 ∣A∣=0
并且A可逆的时候有 A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\frac{1}{|A|}A^* A−1=∣A∣1A∗
2.逆矩阵的性质和公式
- ( A − 1 ) − 1 = A (A^{-1})^{-1}=A (A−1)−1=A
- ( k A ) − 1 = 1 k A − 1 (kA)^{-1}=\frac{1}{k}A^{-1} (kA)−1=k1A−1
- ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
- 若AT可逆,则 ( A T ) − 1 = ( A − 1 ) T (A^T)^{-1}=(A^{-1})^T (AT)−1=(A−1)T
- ∣ A − 1 ∣ = ∣ A ∣ − 1 |A^{-1}|=|A|^{-1} ∣A−1∣=∣A∣−1
3.逆矩阵的计算
抽象形:
- 找到矩阵B使得AB=E,则A-1=B
- 将A分解为若干个可逆矩阵的乘积, A = B C → A − 1 = C − 1 B − 1 A=BC\to A^{-1}=C^{-1}B^{-1} A=BC→A−1=C−1B−1
具体形:
- A − 1 = 1 ∣ A ∣ A ∗ A^{-1}= \frac1{|A|}A^* A−1=∣A∣1A∗(适用于规模位于3阶及以下的矩阵)
- 使用初等行变换求矩阵的逆矩阵,即 [ A ∣ E ] → [ E ∣ A − 1 ] [A|E]\to[E|A^{-1}] [A∣E]→[E∣A−1]
分块矩阵求逆:

这是根据 [ A ∣ E ] → [ E ∣ A − 1 ] [A|E]\to[E|A^{-1}] [A∣E]→[E∣A−1]结合方程组推导出来的, − C − 1 D B − 1 -C^{-1}DB^{-1} −C−1DB−1可以记作为左乘同行,右乘同列,然后取反
n阶对角\副对角矩阵求逆
2.4 伴随矩阵

需要注意的是,伴随矩阵内代数余子式Aij的位置是在j行i列而非i行j列
性质和重要公式
对任意n阶方阵A都有伴随矩阵A*,有 A A ∗ = A ∗ A = ∣ A ∣ E AA^*=A^*A=|A|E AA∗=A∗A=∣A∣E并且 ∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^*|=|A|^{n-1} ∣A∗∣=∣A∣n−1
当 ∣ A ∣ ≠ 0 |A|\neq0 ∣A∣=0的时候,有
- A ∗ = ∣ A ∣ A − 1 ⇔ A − 1 = 1 ∣ A ∣ A ∗ ⇔ A = ∣ A ∣ ( A ∗ ) − 1 A^*=|A|A^{-1}\Leftrightarrow A^{-1}=\frac{1}{|A|}A^*\Leftrightarrow A=|A|(A^*)^{-1} A∗=∣A∣A−1⇔A−1=∣A∣1A∗⇔A=∣A∣(A∗)−1
- ( k A ) ( k A ) ∗ = ∣ k A ∣ E (kA)(kA)^*=|kA|E (kA)(kA)∗=∣kA∣E,此处的kA可替换为A-1、A*
- ∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^*|=|A|^{n-1} ∣A∗∣=∣A∣n−1,可递推为 ( A ∗ ) ∗ = ∣ A ∣ n − 2 A (A^*)^*=|A|^{n-2}A (A∗)∗=∣A∣n−2A,并且有 ∣ ( A ∗ ) ∗ ∣ = ∣ A ∣ ( n − 1 ) 2 |(A^*)^*|=|A|^{(n-1)^2} ∣(A∗)∗∣=∣A∣(n−1)2
- A*的秩相关
- ( A B ) ∗ = B ∗ A ∗ (AB)^*=B^*A^* (AB)∗=B∗A∗
2.5 初等变换和初等矩阵
1.行列式初等变换和矩阵初等变换的异同
- 行列式两行/列互换,行列式值反号;矩阵两行/列互换,矩阵不变
- 行列式值乘以k倍,相当于行列式的某行/列乘以k倍;n阶矩阵乘以k倍,相当于矩阵中每一行乘k倍
- 行列式和矩阵的某行/列加上k倍的另外一行/列,行列式和矩阵都不变
2.初等矩阵性质
- 初等矩阵的转置仍是初等矩阵
- 初等矩阵都是可逆矩阵,其逆矩阵仍然是同一类型初等矩阵
- 如果A是可逆矩阵,则A可以表示成有限个初等矩阵的乘积
3.判断正交以及矩阵正交化
TIPS:
若干个初等矩阵相乘,可凑成一个可逆矩阵
2.6 秩
1.定义

2.公式
-
A是m x n矩阵,则 0 ≤ r ( A ) ≤ m i n ( m , n ) 0\leq r(A)\leq min(m,n) 0≤r(A)≤min(m,n)
-
r ( k A ) = r ( A ) r(kA)=r(A) r(kA)=r(A)
-
P和Q是可逆矩阵,则 r ( A ) = r ( P A ) = r ( P A Q ) r(A)=r(PA)=r(PAQ) r(A)=r(PA)=r(PAQ),也就是A作初等变换不改变秩的值。同理可知,r(AB)<r(A),则r(B)<n,也就是B不可逆
-
r ( A B ) ≤ m i n ( r ( A ) , r ( B ) ) r(AB)\leq min(r(A),r(B)) r(AB)≤min(r(A),r(B))
-
r ( A + B ) ≤ ( [ A ∣ B ] ) ≤ r ( A ) + r ( B ) r(A+B)\leq ([A|B])\leq r(A)+r(B) r(A+B)≤([A∣B])≤r(A)+r(B)
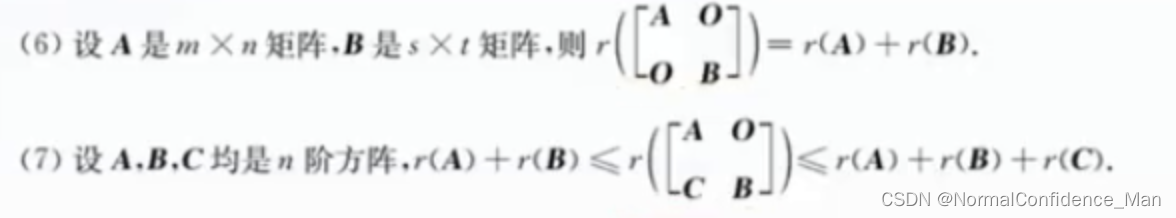
-
设A为m x n矩阵,AB=O,则 r ( A ) + r ( B ) ≤ n r(A)+r(B)\leq n r(A)+r(B)≤n
-
设A为m x n矩阵, r ( A ) = r ( A T ) = r ( A A T ) = r ( A T A ) r(A)=r(A^T)=r(AA^T)=r(A^TA) r(A)=r(AT)=r(AAT)=r(ATA)(四秩相同)

根据上述推导可得出,设A为n阶方阵
n=2时, ( A ∗ ) ∗ = A (A^*)^*=A (A∗)∗=A
n>2时,如果A是可逆矩阵,则 ( A ∗ ) ∗ = ∣ A ∣ n − 2 A (A^*)^*=|A|^{n-2}A (A∗)∗=∣A∣n−2A
n>2时,如果A是不可逆矩阵,则 ( A ∗ ) ∗ = O (A^*)^*=O (A∗)∗=O -
A为n阶方阵,A2=A,可得r(A)+r(A+E)=n
-
A为n阶方阵,A2=E则 r ( A + E ) + r ( A − E ) = n r(A+E)+r(A-E)=n r(A+E)+r(A−E)=n
-
三秩相等:A的秩=A的行秩=A的列秩
3.考法
用阶梯型
将矩阵化为阶梯型矩阵
2.7 矩阵相关题型
1. A n A^n An的题目类型
(1) A是方阵
若A可拆分为 α β T \alpha\beta^T αβT,则r(A)=1,这种情况下,有:
A n = α ( β T α ) ( β T α ) . . . . ( β T α ) β T = [ t r ( A ) ] n − 1 ∗ A A^n=\alpha(\beta^T\alpha)(\beta^T\alpha)....(\beta^T\alpha)\beta^T=[tr(A)]^{n-1}*A An=α(βTα)(βTα)....(βTα)βT=[tr(A)]n−1∗A
(2)使用 A 2 , A 3 A^2,A^3 A2,A3推算出规律
最典型的两种情况是A2=kA或者A2=kE,
注意:矩阵的行列基本变换可能会破坏该规律,因此拿到题后,最好先不要进行行列基本变换
(3)A分解为B和C
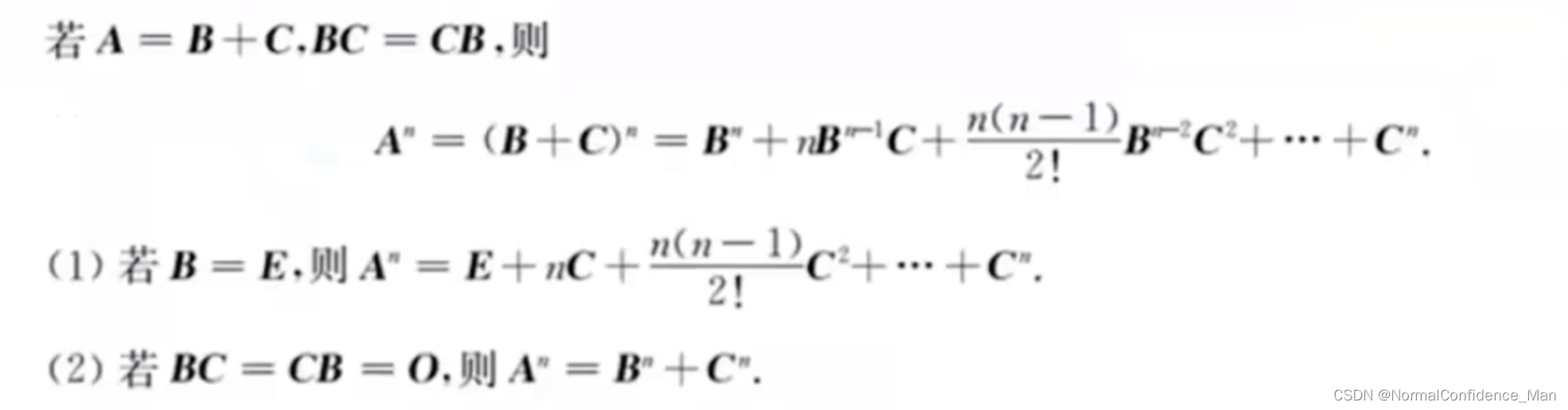
(4)用初等矩阵求P1nAP2m
如果P1和P2是初等矩阵,则P1nAP2m表示对A作n次P1的初等行变换和m次P2的初等列变换
(5)用相似理论求An(重点)
如果 A B A~B A B,也就是A=P-1BP,则An=P-1BnP,
如果 A ∼ λ A\sim \lambda A∼λ,则 A n = P − 1 Λ n P A_n=P_{-1}\Lambda_nP An=P−1ΛnP
在题目要求的矩阵A的n次方无法直接求解的时候,使用求特征值和特征向量,求出其相似矩阵,使用相似矩阵代替A来求n阶矩阵
2.矩阵方程
矩阵方程式含有未知矩阵的方程
基本化简手段
- 消除\提取公因式
- 移项
- 使用公式
求解
1.通过左右同乘分解为 X = A − 1 B , X = B A − 1 , X = A − 1 C B X=A^{-1}B,X=BA^{-1},X=A^{-1}CB X=A−1B,X=BA−1,X=A−1CB
2.如果A不可逆,比如AX=B,可以将X和B按列分块,转化为求线性方程组
3.如果上面都不行,则应该设未知矩阵 X = ( x i j ) X=(x_{ij}) X=(xij),直接代入方程到含未知量为xij的线性方程组,从而求的X