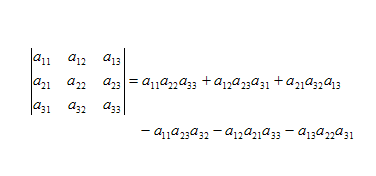线性代数真是一个很抽象的东西,即使我们很多人都学过,但是我相信绝大部分的都不知道这是干嘛用的,找了不少资料,终于发现了这么一篇好文章,于是强烈希望可以和大家分享,帮助大伙进一步理解矩阵的行列式和秩的本质意义。
1 关于面积:
一种映射 大家会说,面积,不就是长乘以宽么,其实不然。我们首先明确,这里所讨论的面积,是欧几里得空间几何面积的基本单位:平行四边形的面积。平行四边形面积的定义,几何上说是相邻两边边长乘以他们之间的夹角的正弦。 然而为了应对更一般情形和更高维度的数理问题,我们有必要把面积的定义推广开来。注意到以下事实: 面积是一个标量,它来自于(构成其相邻边)两个矢量。因此,我们可以将面积看成一个映射:
其中V就是一个矢量,V*V代表两个矢量的有序对;f就是面积的值。 下面我们将说明这个映射是一个线性映射。 从最简单的例子出发。如果第一个矢量是(1,0),第二个矢量是(0,1);也就是说,两个矢量分别是X和Y轴上的单位正向量,那么由这两个矢量张成的四边形就是一个正方形,其面积根据定义,就是长乘以宽=1*1=1。


最后,我们要说明,面积映射对于其操作数(矢量)的矢量加法也是线性的。因为矢量加法操作的本身是线性的,那么其面积映射理应对此也是一个线性映射。这里我们打算从几个实际的例子出发,说明映射的加法线性性的后果。 显然(两个共线矢量所张成的平行四边形还是一条线,因此面积为0):
假定面积映射是一个关于矢量加法的线性映射,那么我们有:
这说明注意计算过程中用到了下面的结论:
也就是说,交换相互垂直操作数矢量的顺序,面积映射取负。孰正孰负取决于认为的定义。一般,我们把X轴单位矢量在前,Y轴单位矢量在后,从X轴到Y轴张成的一个平行四边形的面积,取做正号。
1.1 右手定则
由此我们引入右手定则。注意右手定则只在三维空间中有效。如果以X正方向为首,Y正方向为尾,右手定则告诉我们,纸面向外是面积的正方向;如果反过来,那么纸面向内就是该面积的正方向,与规定的正方向相反,取负号。那么面积正负号的几何意义就明显了。 由此,我们不难得到平面内任意两个矢量所张成的平行四边形的面积(*):
我们不难看到,所谓面积就是一个2X2矩阵的行列式:
如下图。
其中第一行就是我们的第一个行向量(a,b);第二行就是第二个行向量(c,d)。或者第一列是第一个列向量(a,b)^T, 第二列是第二个列向量(c,d)^T。这取决于我们把矢量写成行向量(前者)还是列向量(后者)的形式。
1.2 行列式的计算性质
由此我们很容易能发现,行列式的值与把矢量写成列向量横排还是行向量竖排的方式是无关的。这也就是为什么说,在计算行列式时,行和列的地位是对等的。并且注意到,由上述分析,交换矢量的顺序,面积的值取负号,这也就是为什么行列式中,交换列向量或者行向量一次,就要取一次负号的原因。另外,行列式的其他计算性质,都一一反映在面积映射的线性性之中。 由此我们可见,行列式就是关于“面积”的推广。他就是在给定一组基下,N个向量张成的一个N维广义四边形的体积。这就是行列式的本质含义。
2,行列式的推广
由上,我们可以轻松推广到三维体积的计算:
注意到,行列式的定义,是每一行各取一个不同列的元素的乘积并且符号和所谓的逆序性有关(PARITY)。所谓逆序性,其几何意义就是在规定了一个正方向之后(比如从1,2,3,4,5...N这个顺序定义为正号),交换任意一对数都取一次负号。这样的性质我们在上述的面积函数中已经有所看到,实际上体积,更高维度的广义体积,也有正方向之说,只不过已经难以用右手法则(以及叉乘)来形象说明罢了。右手定则的局限性也是将高维面积推广成行列式表达的一个动机之一。
对于这种交换任何一对指标(操作数)就改变符号的性质,我们叫做:反对称(ANTISYMMETRIC)性。之所以要取不同行不同列元素的乘积,是因为如果有任意两个元素是同行(列)的,那么交换他们的列指标,乘积不变但符号要相反,这乘积必须是0,也就是在行列式的值中不予体现。
行列式的定义之所以这么冗杂,就是来自于面积映射的反对称性。实际上面积映射是一个2-FORM,把2-FORM拓展到任意的R-FORM,我们能看到R-FORM的形式和一个R乘R矩阵的行列式是完全一致的。
由上我们已经可以看到,2-FORM代表的是平面内的面积;3-FORM自然而然就是3维空间内的体积;4-FORM是4维空间里的超体积。以此类推。而实际上,由上我们已经看到,将这些矢量在给定的基坐标下写成矩阵(必定是方阵),矩阵的行列式就是对应的面积(体积)。这个推广的证明各位应该能在任何一本线性代数的专门教材中看到(如果没有的话可以自证)。
3,线性无关的几何意义
记空间的维度为N,给定一组矢量,什么是他们线性无关性?我们下面将说明,一组矢量的线性相关性本质上,是描述他们所张成的广义平行四边形体积是否为NULL(零)。
我们仍然从最简单的2维空间出发。如果两个2维空间的向量是线性相关的,那么就是说,其中一个与另外一个共线,也就是说,他们所张成的四边形,面积是零。反之,如果线性无关,则不共线,则面积不为零。
同理,如果三个三维空间的向量是线性无关的,那么他们三者就不共面。因此他们所张成的平行六面体,体积不是零。
更进一步地,我们知道,二维空间如果给定三个向量,他们必定共面(二维空间内不可能存在一个“体积”),因此他们必定线性相关。推而广之,我们不难理解,为什么一个维度为N的空间内,任意一组M个向量(M>N)必定线性相关了:因为维度大于空间维度的超平形四边体不存在。
由此我们得到一个一一对应的关系:
N
个向量线性无关
==
他们所张成的
N
维体体积不为零
反之,如果N个向量线性相关,那么他们所张成N维体,体积为零。例如,一对共线矢量张成的平行四边形,退化成一个线,其面积显然是0;一组共面的三个矢量张成的平行六面体,退化成一个面,其体积显然是0。
因为我们已经知道行列式与面积的关系,因此我们有结论:
线性无关矢量组成的矩阵的行列式不为零;线性相关矢量组成的矩阵的行列式必为零。
4,行列式与矩阵的逆
我们知道,行列式为0的矩阵,不可逆;行列式不为零的矩阵,可逆。注意我们为简便起见,只讨论方阵的行列式。因此我们不禁要问,代表面积的行列式,是如何和线性变换的可逆性联系在一起的呢?
当我们理解了线性变换的几何意义之后,就不难解答了。我们现陈述如下:
记线性变换的矩阵为A。
如果我们把空间中一组线性无关的矢量都写成列向量的形式,那么他们所张成的N维体体积不为零,根据上面的分析,其值由行列式给出。向量经过线性变换A变换之后,得到的新向量形式如下:
注意到A是一个N*N的矩阵,向量是列向量。
变换前,N维体的体积是:
变换之后,N维体的体积是(注意到,第二个等式实际上说明了几何意义是如何定义矩阵乘法的,也就是N*N矩阵A和另外一个N个列向量组成的N*N矩阵的乘法):
A的行列式如果不为零,则代表这个变换后,N维体的体积不是NULL。又结合线性无关与体积的性质,我们可以说:
如果A的行列式不为零,那么A可以把一组线性无关的矢量,映射成一组新的,线性无关的矢量;A是可逆的(一对一的映射,保真映射,KERNEL是{0})
如果A的行列式为零,那么A就会把一组线性无关的矢量,映射成一组线性相关的矢量;A就不是可逆的(非保真映射,KERNEL不是{0}。我们可以研究他的陪集)
如果A的行列式为负数,那么A将会改变原N维体体积的朝向。
从线性无关到线性相关,其中丢失了部分信息,因此这个变换显然就是不可逆的。线性是否无关和所张成N维体的体积有直接关系,这个体积值又与A的行列式有关。因此我们就建立了A的行列式与其是否可逆的几何关系。
举例说明,我们假设A是一个3维的矩阵。如果映射前,有一组三个线性无关的矢量,我们知道它们张成的体积不是0;经过映射后,他们对应的新矢量也能张成一个平行六面体,那么这个平行六面体的体积就是原体积乘以A的行列式。
显然,如果A的行列式是0,那么变换后的新“平行六面体"的体积将不可避免的也是0。根据上文的结论,我们有:变换后的这一组新矢量线性相关。
结论:
线性变换A的行列式是否为零,就代表了其映射的保真性,也即,能不能把一组线性无关的矢量变换成另一组保持无关性的矢量。
5.秩
有时候,虽然A并不能保持把空间一组最大数目矢量的线性无关性,但它能保证一组更少数目矢量的线性无关性。这个数目往往少于A的维度(或者说,线性空间的维度),这个数目就叫做线性变换A的秩。
例如,一个秩为2的三乘三矩阵A。因为秩小于3,那么任何一个3维六面体经过他的变换后,体积都为零(退化一个面);但存在一个面积不为零的面,在变换之后还可以是一个非零面积的面。
所谓一个线性变换的秩,无非就是变换后,还能保持非零体积的几何形状的最大维度。
理解了秩,行列式和可逆性的几何意义,我们就能随意构造一些线性变换A,使得他要么保全所有的几何体,要么将特定维度特定结构的几何体,压缩成更低维度的几何体。这不就是所谓的“降维打击”么。。所 以说,三体中的终极必杀,其实也就是一个行列式为0,秩比维度少1的一个线性变换而已。