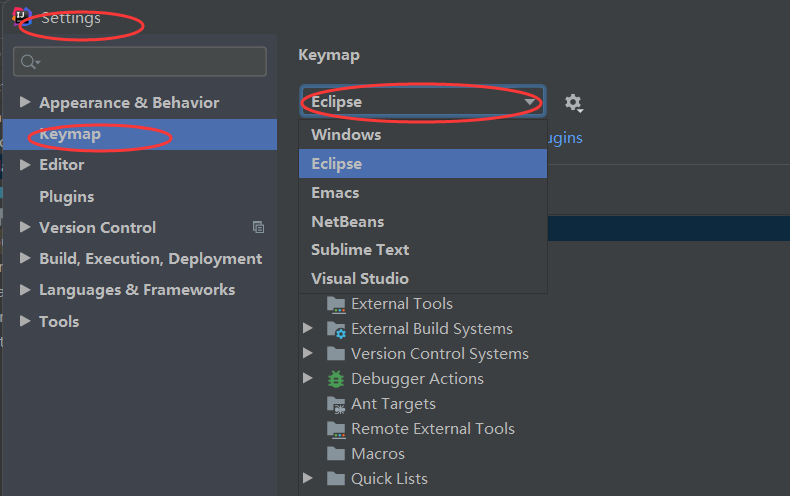
一 算法原理
雅可比方法用于求解实对称矩阵的特征值和特征向量,对于实对称矩阵 A A A,必有正交矩阵 U U U,使得 U T A U = D U^{T}AU=D UTAU=D. D D D是一个对角阵,主对角线的元素是矩阵 A A A的特征值,正交矩阵 U U U的每一列对应于属于矩阵 D D D的主对角线对应元素的特征向量.
雅可比方法用平面旋转对矩阵 A A A做相似变换,化 A A A为对角阵,从而求解出特征值和特征向量.旋转矩阵 U p q U_p{_q} Upq,是一个单位阵在第 p p p行,第 p p p列,第 q q q行,第 q q q列,元素为 c o s φ cos\varphi cosφ,第 p p p行第 q q q列为 − s i n φ -sin\varphi −sinφ,第 q q q行第 p p p列为 s i n φ sin\varphi sinφ.对于这样的平面旋转矩阵,不难验证其是一种正交矩阵.因此对于向量 x x x, U p q x U_p{_q}x Upqx等同于把第 p p p个坐标轴和第 q q q个坐标轴共同所确定的平面旋转了 φ \varphi φ度.记矩阵 A 1 = U p q T A U p q A_1=U_p{_q}^{T}AU_p{_q} A1=UpqTAUpq.因为旋转矩阵是正交阵,因此实际上矩阵 A 1 A_1 A1与矩阵 A A A是相似的,因此其特征值是相同的.
设矩阵 A 1 A_1 A1第 i i i行,第 j j j列的元素为 b i j b_i{_j} bij,矩阵 A A A的第 i i i行,第 j j j列的元素为 a i j a_i{_j} aij( i = 0 , 1 , 2 , . . . , n − 1 , j = 0 , 1 , 2 , . . . , n − 1 i=0,1,2,...,n-1,j=0,1,2,...,n-1 i=0,1,2,...,n−1,j=0,1,2,...,n−1).式(1-1-1)给出了两矩阵元素之间的运算关系.
{ b p p = a p p c o s 2 φ + a q q s i n 2 φ + 2 a p q c o s φ s i n φ b q q = a p p s i n 2 φ + a q q c o s 2 φ − 2 a p q c o s φ s i n φ b p q = b q p = 1 2 ( a q q − a p p ) s i n 2 φ + a p q c o s 2 φ b p i = a p i c o s φ + a q i s i n φ , ( i ≠ p , q ) b q i = − a p i s i n φ + a q i c o s φ , ( i ≠ p , q ) b j p = a j p c o s φ + a j q s i n φ , ( j ≠ p , q ) b j q = − a j q s i n φ + a j q c o s φ , ( j ≠ p , q ) b i j = b j i = a i j , i ≠ p , q ; j ≠ p , q (1-1-1) \begin{cases} b_p{_p}=a_p{_p}cos^2\varphi+a_q{_q}sin^2\varphi+2a_p{_q}cos\varphi{sin\varphi}\\ b_q{_q}=a_p{_p}sin^2\varphi+a_q{_q}cos^2\varphi-2a_p{_q}cos\varphi{sin\varphi}\\ b_p{_q}=b_q{_p}=\frac{1}2(a_q{_q}-a_p{_p})sin2\varphi+a_p{_q}cos2\varphi\\ b_p{_i}=a_p{_i}cos\varphi+a_q{_i}sin\varphi,(i\ne{p},q)\\ b_q{_i}=-a_p{_i}sin\varphi+a_q{_i}cos\varphi,(i\ne{p},q)\\ b_j{_p}=a_j{_p}cos\varphi+a_j{_q}sin\varphi,(j\ne{p},q)\\ b_j{_q}=-a_j{_q}sin\varphi+a_j{_q}cos\varphi,(j\ne{p},q)\\ b_i{_j}=b_j{_i}=a_i{_j},i{\ne}p,q;j{\ne}p,q \end{cases} \tag{1-1-1} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧bpp=appcos2φ+aqqsin2φ+2apqcosφsinφbqq=appsin2φ+aqqcos2φ−2apqcosφsinφbpq=bqp=21(aqq−app)sin2φ+apqcos2φbpi=apicosφ+aqisinφ,(i=p,q)bqi=−apisinφ+aqicosφ,(i=p,q)bjp=ajpcosφ+ajqsinφ,(j=p,q)bjq=−ajqsinφ+ajqcosφ,(j=p,q)bij=bji=aij,i=p,q;j=p,q(1-1-1)
其中有两点需要说明:(1) p p p, q q q分别是前一次的迭代矩阵的非主对角线上绝对值最大元素的行列号
(2) φ \varphi φ是旋转角度,可以由式(1-1-2)确定
t a n 2 φ = − 2 a p q a q q − a p p (1-1-2) tan2\varphi=\frac{-2a_p{_q}}{a_q{_q}-a_p{_p}} \tag{1-1-2} tan2φ=aqq−app−2apq(1-1-2)
归纳得到雅可比方法求解矩阵特征值和特征向量的具体步骤如下:
(1).初始化特征向量为对角阵V,主对角线元素为1,其他元素为0.
(2).在 A A A的非主对角线的元素中,找到绝对值最大元素 a p q a_p{_q} apq.
(3).用式(1-1-2)计算出旋转矩阵
(4).计算矩阵 A 1 A1 A1,用当前的矩阵 V V V乘旋转矩阵得到当前的特征矩阵 V V V.
(5).若当前迭代的矩阵 A A A的非主对角线元素最大值小于给定阈值,停止计算,否则执行上述过程.停止计算时,特征值为矩阵 A A A的主对角线元素,特征矩阵为矩阵 V V V.
二 C语言实现
#include<stdio.h>
#include<stdlib.h>
float** Matrix_Jac_Eig(float **array, int n, float *eig);
int Matrix_Free(float **tmp, int m, int n);
int main(void)
{int n;printf("请输入矩阵维度:\n");scanf("%d", &n);float **array = (float **)malloc(n * sizeof(float *));if (array == NULL){printf("error :申请数组内存空间失败\n");return -1;}for (int i = 0; i < n; i++){array[i] = (float *)malloc(n * sizeof(float));if (array[i] == NULL){printf("error :申请数组子内存空间失败\n");return -1;}}printf("请输入矩阵元素:\n");for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){scanf("%f", &array[i][j]);}}float *eig = (float *)malloc(n * sizeof(float));float **Result = Matrix_Jac_Eig(array, n, eig);printf("特征矩阵元素:\n");for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){printf("%f ", Result[i][j]);}printf("\n");}printf("特征矩阵元素:\n");for (int i = 0; i < n; i++){printf("%f \n", eig[i]);}Matrix_Free(Result, n, n);free(eig);eig = NULL;return 0;
}
float** Matrix_Jac_Eig(float **array, int n, float *eig)
{//先copy一份array在temp_mat中,因为我实在堆区申请的空间,在对其进行处理//的过程中会修改原矩阵的值,因此要存储起来,到最后函数返回的//时候再重新赋值int i, j, flag, k;flag = 0;k = 0;float sum = 0;float **temp_mat = (float **)malloc(n * sizeof(float *));for (i = 0; i < n; i++){temp_mat[i] = (float *)malloc(n * sizeof(float));}for (i = 0; i < n; i++){for (j = 0; j < n; j++){temp_mat[i][j] = array[i][j];}}//判断是否为对称矩阵for (i = 0; i < n; i++){for (j = i; j < n; j++){if (array[i][j] != array[j][i]){flag = 1;break;}}}if (flag == 1){printf("error in Matrix_Eig: 输入并非是对称矩阵:\n");return NULL;}else{//开始执行算法int p, q;float thresh = 0.0000000001;float max = array[0][1];float tan_angle, sin_angle, cos_angle;float **result = (float **)malloc(n * sizeof(float *));if (result == NULL){printf("error in Matrix_Eig:申请空间失败\n");return NULL;}float **result_temp = (float **)malloc(n * sizeof(float *));if (result_temp == NULL){printf("error in Matrix_Eig:申请空间失败\n");return NULL;}float **rot = (float **)malloc(n * sizeof(float *));if (rot == NULL){printf("error in Matrix_Eig:申请空间失败\n");return NULL;}float **mat = (float **)malloc(n * sizeof(float *));if (mat == NULL){printf("error in Matrix_Eig:申请空间失败\n");return NULL;}for (i = 0; i < n; i++){result[i] = (float *)malloc(n * sizeof(float));if (result[i] == NULL){printf("error in Matrix_Eig:申请子空间失败\n");return NULL;}result_temp[i] = (float *)malloc(n * sizeof(float));if (result_temp[i] == NULL){printf("error in Matrix_Eig:申请子空间失败\n");return NULL;}rot[i] = (float *)malloc(n * sizeof(float));if (rot[i] == NULL){printf("error in Matrix_Eig:申请子空间失败\n");return NULL;}mat[i] = (float *)malloc(n * sizeof(float));if (mat[i] == NULL){printf("error in Matrix_Eig:申请子空间失败\n");return NULL;}}for (i = 0; i < n; i++){for (j = 0; j < n; j++){if (i == j){result[i][j] = 1;}else{result[i][j] = 0;}}}for (i = 0; i < n; i++){for (j = 0; j < n; j++){if (i == j){mat[i][j] = 1;}else{mat[i][j] = 0;}}}max = array[0][1];for (i = 0; i < n; i++){for (j = 0; j < n; j++){if (i == j){continue;}else{if (fabs(array[i][j]) >= fabs(max)){max = array[i][j];p = i;q = j;}else{continue;}}}}while (fabs(max) > thresh){if (fabs(max) < thresh){break;}tan_angle = -2 * array[p][q] / (array[q][q] - array[p][p]);sin_angle = sin(0.5*atan(tan_angle));cos_angle = cos(0.5*atan(tan_angle));for (i = 0; i < n; i++){for (j = 0; j < n; j++){if (i == j){mat[i][j] = 1;}else{mat[i][j] = 0;}}}mat[p][p] = cos_angle;mat[q][q] = cos_angle;mat[q][p] = sin_angle;mat[p][q] = -sin_angle;for (i = 0; i < n; i++){for (j = 0; j < n; j++){rot[i][j] = array[i][j];}}for (j = 0; j < n; j++){rot[p][j] = cos_angle*array[p][j] + sin_angle*array[q][j];rot[q][j] = -sin_angle*array[p][j] + cos_angle*array[q][j];rot[j][p] = cos_angle*array[j][p] + sin_angle*array[j][q];rot[j][q] = -sin_angle*array[j][p] + cos_angle*array[j][q];}rot[p][p] = array[p][p] * cos_angle*cos_angle +array[q][q] * sin_angle*sin_angle +2 * array[p][q] * cos_angle*sin_angle;rot[q][q] = array[q][q] * cos_angle*cos_angle +array[p][p] * sin_angle*sin_angle -2 * array[p][q] * cos_angle*sin_angle;rot[p][q] = 0.5*(array[q][q] - array[p][p]) * 2 * sin_angle*cos_angle +array[p][q] * (2 * cos_angle*cos_angle - 1);rot[q][p] = 0.5*(array[q][q] - array[p][p]) * 2 * sin_angle*cos_angle +array[p][q] * (2 * cos_angle*cos_angle - 1);for (i = 0; i < n; i++){for (j = 0; j < n; j++){array[i][j] = rot[i][j];}}max = array[0][1];for (i = 0; i < n; i++){for (j = 0; j < n; j++){if (i == j){continue;}else{if (fabs(array[i][j]) >= fabs(max)){max = array[i][j];p = i;q = j;}else{continue;}}}}for (i = 0; i < n; i++){eig[i] = array[i][i];}for (i = 0; i < n; i++){for (j = 0; j < n; j++){sum = 0;for (k = 0; k < n; k++){sum = sum + result[i][k] * mat[k][j];}result_temp[i][j] = sum;}}for (i = 0; i < n; i++){for (j = 0; j < n; j++){result[i][j] = result_temp[i][j];}}}for (i = 0; i < n; i++){for (j = 0; j < n; j++){array[i][j] = temp_mat[i][j];}}Matrix_Free(result_temp, n, n);Matrix_Free(rot, n, n);Matrix_Free(mat, n, n);Matrix_Free(temp_mat, n, n);return result;}
}
int Matrix_Free(float **tmp, int m, int n)
{int i, j;if (tmp == NULL){return(1);}for (i = 0; i < m; i++){if (tmp[i] != NULL){free(tmp[i]);tmp[i] = NULL;}}if (tmp != NULL){free(tmp);tmp = NULL;}return(0);
}
三 结果
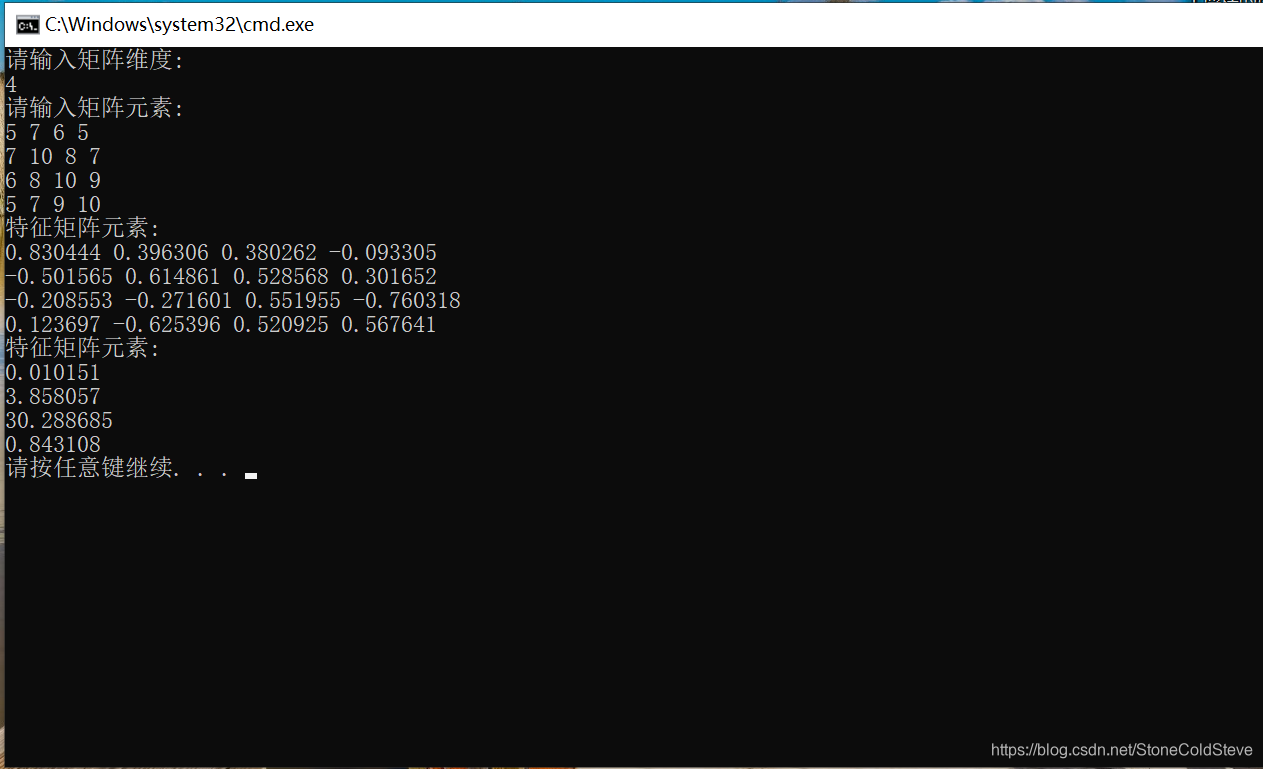




![[IDE]IntelliJ IDEA使用教程(很全)](https://img-blog.csdn.net/20170710160958729)