目录
- 1. 应用场景-修路问题
- 2. 最小生成树
- 3. 普里姆算法介绍
- 4. 代码实现
1. 应用场景-修路问题
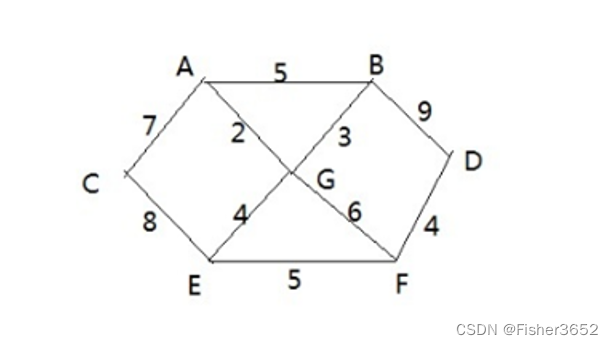
- 有7个村庄(A, B, C, D, E, F, G) ,现在需要修路把7个村庄连通
- 各个村庄的距离用边线表示(权) ,比如 A – B 距离 5公里
- 问:如何修路保证各个村庄都能连通,并且总的修建公路总里程最短?
思路: 将10条边,连接即可,但是总的里程数不是最小.
正确的思路,就是尽可能的选择少的路线,并且每条路线最小,保证总里程数最少.
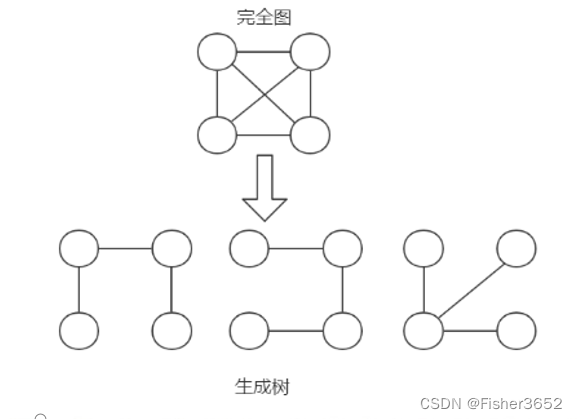
2. 最小生成树
- 修路问题本质就是就是最小生成树问题,最小生成树(Minimum Cost Spanning Tree),简称MST。
- 给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树
- N个顶点,一定有N-1条边
- 包含全部顶点
- N-1条边都在图中
- 举例说明(如图:)
- 求最小生成树的算法主要是普里姆算法和克鲁斯卡尔算法
3. 普里姆算法介绍
- 普利姆(Prim)算法求最小生成树,也就是在包含n个顶点的连通图中,找出只有(n-1)条边包含所有n个顶点的连通子图,也就是所谓的极小连通子图
- 普利姆的算法如下
- 设G=(V,E)是连通网,T=(U,D)是最小生成树,V,U是顶点集合,E,D是边的集合
- 若从顶点u开始构造最小生成树,则从集合V中取出顶点u放入集合U中,标记顶点v的visited[u]=1
- 若集合U中顶点ui与集合V-U中的顶点vj之间存在边,则寻找这些边中权值最小的边,但不能构成回路,将顶点vj加入集合U中,将边(ui,vj)加入集合D中,标记visited[vj]=1
- 重复步骤②,直到U与V相等,即所有顶点都被标记为访问过,此时D中有n-1条边
- 思路分析
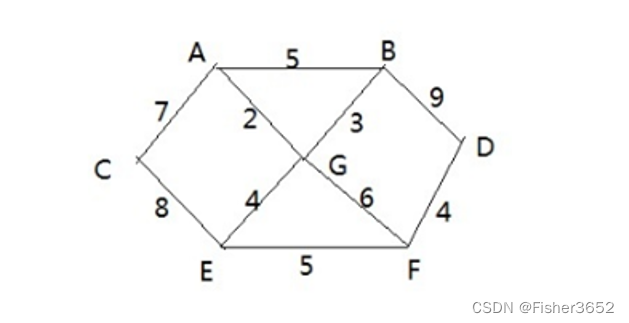
1.从A顶点开始处理 => <A,G> 2
A-C [7] A-G[2] A-B[5]
2.<A,G> 开始 , 将A 和 G 顶点和他们相邻的还没有访问的顶点进行处理 =><A,G,B>
A-C[7] A-B[5] G-B[3] G-E[4] G-F[6]
3.<A,G,B> 开始,将A,G,B 顶点 和他们相邻的还没有访问的顶点进行处理=><A,G,B,E>
A-C[7] G-E[4] G-F[6] B-D[9]
…
4.{A,G,B,E}->F//第4次大循环 , 对应边<E,F> 权值:5
5.{A,G,B,E,F}->D//第5次大循环 , 对应边<F,D> 权值:4
6.{A,G,B,E,F,D}->C//第6次大循环 , 对应边<A,C> 权值:7 => <A,G,B,E,F,D,C>
4. 代码实现
import java.util.Arrays;public class PrimAlgorithm {public static void main(String[] args) {char[] data = new char[]{'A', 'B', 'C', 'D', 'E', 'F', 'G'};int num = data.length;// 邻接矩阵的关系使用二维数组表示,使用10000这个比较大的数值表示两点不连通int[][] weight = new int[][]{{10000, 5, 7, 10000, 10000, 10000, 2},{5, 10000, 10000, 9, 10000, 10000, 3},{7, 10000, 10000, 10000, 8, 10000, 10000},{10000, 9, 10000, 10000, 10000, 4, 10000},{10000, 10000, 8, 10000, 10000, 5, 4},{10000, 10000, 10000, 4, 5, 10000, 6},{2, 3, 10000, 10000, 4, 6, 10000}};// 创建图MGraph graph = new MGraph(num);// 创建一个minTree对象MinTree minTree = new MinTree();minTree.createGraph(graph, num, data, weight);// 打印图minTree.showGraph(graph);minTree.prim(graph, 0);}static class MGraph {// 表示图的节点数量int num;// 存放节点数据char[] data;// 存放边,即邻接矩阵int[][] weight;public MGraph(int num) {this.num = num;this.data = new char[num];this.weight = new int[num][num];}}// 最小生成树->村庄的图static class MinTree {/*** 创建图的邻接矩阵** @param graph 图* @param num 图对应的节点数量* @param data 图的各个节点的值* @param weight 图的邻接矩阵*/public void createGraph(MGraph graph, int num, char[] data, int[][] weight) {// int i, j;for (int i = 0; i < num; i++) {graph.data[i] = data[i];for (int j = 0; j < num; j++) {graph.weight[i][j] = weight[i][j];}}}// 显示图的邻接矩阵public void showGraph(MGraph graph) {for (int[] link : graph.weight) {System.out.println(Arrays.toString(link));}}/*** prim算法,得到最小生成树** @param graph 图* @param v 表示从图的第几个节点开始生成'A'->0 'B'->1 ...*/public void prim(MGraph graph, int v) {// 标记节点是否被访问过int[] visited = new int[graph.num];// 把当前节点标记为已访问visited[v] = 1;// 使用h1和h2记录两个节点的下标int h1 = -1;int h2 = -2;// 记录最小距离,将minWeight初始成一个大数,后面遍历过程中会被替换int minWeight = 10000;// 因为有graph.num个节点,普利姆算法结束后,有graph.num-1条边for (int k = 1; k < graph.num; k++) {// 确定每一次生成的子图,和哪个节点的距离最近// i节点表示被访问过的节点for (int i = 0; i < graph.num; i++) {// j节点表示没被访问过的节点for (int j = 0; j < graph.num; j++) {if (visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight) {// 替换最小距离minWeight = graph.weight[i][j];h1 = i;h2 = j;}}}// 找到一条距离最短的边System.out.println("边<" + graph.data[h1] + "," + graph.data[h2] + "> 权值:" + minWeight);// 将当前这个节点标记为已访问visited[h2] = 1;// minWeight重新设置为最大值 10000minWeight = 10000;}}}}- 结果打印
[10000, 5, 7, 10000, 10000, 10000, 2]
[5, 10000, 10000, 9, 10000, 10000, 3]
[7, 10000, 10000, 10000, 8, 10000, 10000]
[10000, 9, 10000, 10000, 10000, 4, 10000]
[10000, 10000, 8, 10000, 10000, 5, 4]
[10000, 10000, 10000, 4, 5, 10000, 6]
[2, 3, 10000, 10000, 4, 6, 10000]
边<A,G> 权值:2
边<G,B> 权值:3
边<G,E> 权值:4
边<E,F> 权值:5
边<F,D> 权值:4
边<A,C> 权值:7