模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能控制方法，它是从行为上模仿人的模糊推理和决策过程的一种智能控制算法。模糊控制首先将操作人员或专家经验编成模糊规则，然后将来自传感器的实时信号模糊化，将模糊化后的信号作为模糊规则的输入，完成模糊推理，将推理后得到的输出量加到执行器上。

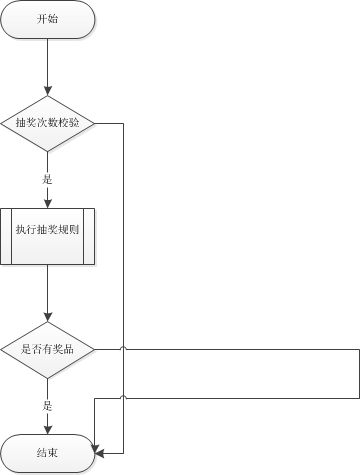
        模糊控制的过程如下图所示。

        上图中，包括了模糊控制的主要过程。关于模糊控制的基本原理，在很多文章中都有介绍，但一般介绍都比较抽象，读者不容易理解。在本文中，我们通过一个简单的例子来进行介绍。

1、模糊化

        以水温的电加热为例，我们对模糊控制进行介绍。在一个容器中装满了水，我们要将水维持在一个恒定的温度，比如：60度。我们控制水温的工具是电加热器。在这个控制系统中，控制算法的输入为温度的偏差，即期望温度与实际温度的插，我们假设这个偏差的范围为[-20, 20]，我们称它为基本论域。算法的输出为电加热的功率，我们假设它的基本论域为[0, 2000]，单位是瓦。

        我们取输入和输出的模糊集合分别为{NB, NS, O, PS, PB}，{NB, NS, O, PS, PB}。其中NB表示负大，NS表示负小，O表示零，PS表示正小，PB表示正大。另外，我们取输入和输出的模糊子集论域为{-4，-3，-2，-1，0，1，2，3，4}，{-3，-2，-1，0，1，2，3}。我们可以得出一般的公式，由基本论域到[a, b]模糊子集论域[-n, n]的转换关系：

        通过上面的公式我们可以将基本论域上的精确至映射到模糊子集论域内，接下来我们要通过隶属度关系计算出我们的输入或输出变量对模糊集合的隶属度，这个过程称为模糊化。隶属度关系我们一般通过隶属度图或隶属度表格来表示。如下图所示，为输入的隶属度图。

用表格表示，如下所示。

	-4	-3	-2	-1	0	1	2	3	4
PB	0	0	0	0	0	0	0	0.5	1
PS	0	0	0	0	0	0.5	1	0.5	0
O	0	0	0	0.5	1	0.5	0	0	0
NS	0	0.5	1	0.5	0	0	0	0	0
NB	1	0.5	0	0	0	0	0	0	0

同样，输出的隶属度关系，用表格表示为

	-3	-2	-1	0	1	2	3
PB	0	0	0	0	0	0.5	1
PS	0	0	0	0	0.5	0.5	0
O	0	0	0.5	1	0.5	0	0
NS	0	0.5	0.5	0	0	0	0
NB	1	0.5	0	0	0	0	0

有了上边的关系，我们就可以将控制算法的输入进行模糊化。比如我们期望的温度是60度，实际的温度为45度，则温度偏差为15度，则对应的模糊子集论域上的取值为：

我们从表中可以看到，3对应PB的隶属度为0.5，PS的隶属度为0.5。这样我们完成了偏差15的模糊化。

2、建立模糊控制规则

        模糊规则是模糊控制算法的核心，它决定了算法的控制规则。在我们这个例子中，如果偏差很大，我们模糊化后为PB，则实际温度比期望温度低很多，这是我们需要用很大的功率来加热，所以控制量为PB；如果实际温度已经达到了期望温度，则输入的温度偏差模糊化后为O，这时，我们为了维持温度，需要用中等的功率来维持温度，所以控制量为O。如果输入量为NB，相应的控制量为NB。所以根据这个原则，我们可以得到模糊控制规则，如下表。

if（若）	NBe	NSe	Oe	PSe	PBe
then（则）	NBu	NSu	Ou	PSu	PBu

3、求模糊关系

      模糊控制规则是一个多条语句，它可以表示为EXU上的模糊子集，即模糊关系R，它通过下面的式子计算。

其中，表示求交集，对于两个数值来说，就是取数值小的数值。表示求并集，对于两个数值来说就是取数值大的数值。NBe、NBu等为最上面的表格中的隶属度的向量，我们进行计算得到下面的结果。

将上面的5个矩阵求并集计算得到模糊关系如下。

4、模糊决策

        模糊控制器的输出为误差向量和模糊关系的合成：

例如，如果误差为PS，则对应的向量

则

5、控制量的反模糊化

        由上面的计算得到

这几个系数，对应于模糊子集论域，一般表示为

注意这个式子只是一个表示方式，不是除的计算。

一般，我们采用重心发来计算控制量的模糊值，如下进行计算

注意这个u的值是模糊子集论域中的值，它的取值范围是[-n, n]，用项目的公式，可以将它转换为[a, b]空间上。

在这个示例中，a=0，b=2000，n=3，U=1。代入公式计算得到u=1333，即需要用1333瓦的功率来进行加热。