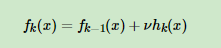前端业务逻辑

1-关于全选和非全选

Vue3环境下
运用ant-design-vue框架

展示效果

全选

非全选

业务逻辑

1、数据结构data

const state = reactive({cart: '', // 购物车信息ids: [], // 删除购物车单个商品的idcartNum: '', // 购物车数量checkAll: false, // 是否处于全选状态checkedList: []
})

2、template层

   
<a-checkbox:checked="state.checkAll"@change="onCheckAllChange"   //--全选的方法
>全选</a-checkbox><tr v-for="(item, index) in state.cart" :key="item.id"><td class="one-check"><a-checkbox:checked="state.checkedList[index]"@change="(e) => onChange(e, index)"   // 复选框的方法/></td>
</tr>

3、提前把checkedList设置为一个数组，并且为数组为false

onMounted(async () => {
// 获取购物车信息并保存到store里const cartInfo = await cart()state.cart = cartInfo.datastore.commit('cart/setCartInfo', cartInfo.data)for (const i in cartInfo.data) {const id = cartInfo.data[i].idstate.ids.push(id)state.checkedList[i] = false    // -----这里是重点！！！-----}state.cartNum = state.cart.length
})

4、全选和复选框的业务逻辑

// 复选框
const onChange = (e, index) => {state.checkedList[index] = e.target.checked// 根据every方法判断isAll里是否全是true，如果是就全选，不是的话就false 非全选const isAll = state.checkedList.every(value => value === true)  isAll ? state.checkAll = true : state.checkAll = false
}
// 全选
const onCheckAllChange = (e) => {state.checkAll = !state.checkAll     // 状态反转// 如果state.checkAll为true，则循环checkedList数组，把勾选的都变为true，设为全选   if (state.checkAll) {state.checkedList.forEach((value, index) => {state.checkedList[index] = true})// 如果state.checkAll为false，则勾选的都变为false，非全选} else {state.checkedList.forEach((value, index) => {state.checkedList[index] = false})}
}