目录
一、什么是GBDT
二、GBDT的理解
2.1、GBDT通俗解释
2.2、GBDT详解
三、GBDT的应用
3.1、二分类问题
3.2、多分类问题
3.3、回归问题
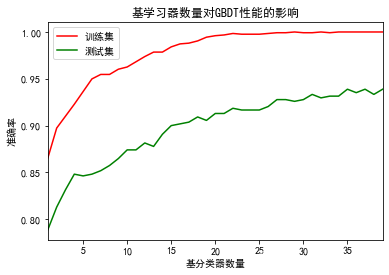
四、GBDT如何选择特征
五、GBDT优缺点
一、什么是GBDT
GBDT,Gardient Boosting Decision Tree,梯度提升树,是一种属于boosting思想的迭代决策树。
提升树是采用前向分布算法训练多个弱学习器,而每个弱学习器用CART回归树构建,然后将多个弱学习器采用加法模型结合起来,作为最终的强学习器。GBDT属于boosting模型,所以每个弱分类器之间是有联系的,GBDT的后一个弱分类器训练的是前一个弱分类器损失的梯度,这样每次迭代都向着损失减小的方向,最终得到最优解。
二、GBDT的理解
2.1、GBDT通俗解释
提升树模型可表示为以决策树为基学习器的加法模型,具体公式为:
其中,表示第m棵决策树,M表示基学习器的数量,
表示第m棵学习器的参数,比如叶子节点个数、树的深度等等。
那么如何求解加法模型呢?这里就要用到前向分布算法了,其实也就是用最直观的迭代求解。
首先初始化:
第m部的模型为:
通过最小化经验风险,也就是损失函数最小化来求解:
这里的L()为损失函数,回归常用的损失函数为MSE、绝对损失、Huber损失和分位数损失。分类常用的损失函数为指数损失和对数损失。
2.2、GBDT详解
上面说到要损失函数最小化,那么如何来进行损失函数最小化呢?梯度下降法是我们首先想到的,当我们进行GBDT回归时,如果损失函数为MSE,那么我们可以很方便的求梯度,找到最优解——残差。残差是指真实值与预测值之间的误差,对于损失函数:,对其求导可得最优解为
,这就是残差的由来。
残差是回归模型的损失为MSE的一种特殊情况,但一般情况下损失函数求导并不方便,前向分布优化并不顺利,因此利用损失函数的负梯度在当前模型的值作为回归问题提升树算法的残差近似值,拟合一个回归树,成为了GDBT的核心思想。
三、GBDT的应用
3.1、二分类问题
二分类GBDT流程如下:




3.2、多分类问题


3.3、回归问题

当使用MSE时,梯度求解就变成了残差,通过后续对残差的优化来拟合训练数据。这里不做详细介绍。
四、GBDT如何选择特征
不论将GBDT用于分类任务还是回归任务,GBDT的基学习器均为CART回归树,因为要拟合每一轮迭代的残差。所以选择特征的问题就变成了CART回归树构造如何选择特征。
但是在机器学习库sklearn中,用于分类的GBDT的基学习器可以用CART回归树,其特征选择可以基于基尼系数。
五、GBDT优缺点
优点:
- 精度高,无论是分类还是回归任务
- 可以处理非线性数据
- 可以处理离散值和连续值
- 使用一些健壮的损失函数,对异常值不敏感。比如 Huber损失函数和Quantile损失函数。
缺点:由于下一个学习器需要拟合上一个学习器的残差,所以必须穿行执行,无法并行,这也导致处理大型数据时速度特别慢。因此后来的XGBoost和LightGBM都是基于GBDT但在并行性上做出了改进。












![java byte[]转int和double](https://img-blog.csdnimg.cn/2b25e72886094f6e80c16aea42d455da.png)

