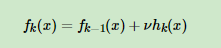梯度提升树的使用

GBDT算法流程

GBDT流程

输入：训练数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } D=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{N}, y_{N}\right)\right\} D={(x1​,y1​),(x2​,y2​),…,(xN​,yN​)}

1.初始化$f_0(x)=0$

2.For $m=1,2,\dots ,M$

3.针对每一个样本$\left(x_i,y_i\right)$，计算残差
$$r_{m,i}=y_i-f_{m-1}\left(x_i\right),i=1,2,\dots ,N$$4.利用 { ( x i , r m , i ) } i = 1 , 2 , … , N \left\{\left(x_{i}, r_{m, i}\right)\right\}_{i=1,2, \ldots, N} {(xi​,rm,i​)}i=1,2,…,N​训练一个决策树（回归树），>得到$T\left(x;{\Theta }_m\right)$

5.更新$f_m(x)=f_{m-1}(x)+T\left(x;{\Theta }_m\right)$

6.完成以上迭代，得到提升树$f_M(x)={\sum }_{m=1}^{M}T\left(x;{\Theta }_m\right)$

---

负梯度和残差

GBDT全称：Gradient Boosting Decision Tree，即梯度提升决策树，理解为梯度提升 + 决策树。Friedman提出了利用最速下降的近似方法，利用损失函数的负梯度拟合集学习器：
$$-{\left[\frac{\partial L\left(y_i,F\left({\mathbf{x}}_{\mathbf{i}}\right)\right)}{\partial F\left({\mathbf{x}}_{\mathbf{i}}\right)}\right]}_{F(\mathbf{x})=F_{t-1}(\mathbf{x})}$$怎么理解这个近似，我们通过平方损失函数来给大家进行介绍

为了求导方便，在损失函数前面乘以1/2
$$L\left(y_i,F\left({\mathbf{x}}_{\mathbf{i}}\right)\right)=\frac{1}{2}{\left(y_i-F\left({\mathbf{x}}_{\mathbf{i}}\right)\right)}^2$$对$F(X_i)$求导，则有：
$$\frac{\partial L\left(y_i,F\left({\mathbf{x}}_{\mathbf{i}}\right)\right)}{\partial F\left({\mathbf{x}}_{\mathbf{i}}\right)}=F\left({\mathbf{x}}_{\mathbf{i}}\right)-y_i$$残差是梯度的相反数，即：
$$r_{ti}=y_i-F_{t-1}(\mathbf{x})=-{\left[\frac{\partial L\left(y_i,F\left({\mathbf{x}}_{\mathbf{i}}\right)\right)}{\partial F\left({\mathbf{x}}_{\mathbf{i}}\right)}\right]}_{F(\mathbf{x})=F_{t-1}(\mathbf{x})}$$在GBDT中使用负梯度作为残差进行拟合。

---

GBDT流程（回归）

GBDT是使用梯度提升的决策树（CART），CART树回归将空间划分为K个不相交的区域，并确定每个区域的输出$c_k$，数学表达如下：
$$f(\mathbf{X})=\sum _{k=1}^K{c}_{k}I\left(\mathbf{X}\in R_k\right)$$

输入：训练数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } D=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{N}, y_{N}\right)\right\} D={(x1​,y1​),(x2​,y2​),…,(xN​,yN​)}
1.初始化：$F_0(\mathbf{x})=\arg {\min }_{h_0}{\sum }_{i=1}^{N}L\left(y_i,h_{\delta }(\mathbf{x})\right)=\arg {\min }_c{\sum }_{i=1}^{N}L\left(y_i,c\right))$

2.for t = 1 to T do

2.1 计算负梯度
$${\tilde{y}}_i=-{\left[\frac{\partial L\left(y_i,F\left({\mathbf{x}}_{\mathrm{i}}\right)\right)}{\partial F\left({\mathbf{x}}_{\mathrm{i}}\right)}\right]}_{F(\mathbf{x})=F_{t-1}(\mathbf{x})},i=1,2,\cdots ,N$$2.2 拟合残差得到回归树，得到第t棵树的叶节点区域：
$$h_t(\mathbf{x})=\sum _{k=1}^K{c}_{k}I\left(\mathbf{X}\in R_{tk}\right)$$2.3更新
$$F_t(\mathbf{x})=F_{t-1}\left({\mathbf{x}}_{\mathbf{i}}\right)+h_t(\mathbf{x})=F_{t-1}\left({\mathbf{x}}_{\mathbf{i}}\right)+\sum _{k=1}^K{c}_{k}I\left(\mathbf{X}\in R_{tk}\right)$$

3.得到加法模型：$\mathbf{F}(\mathbf{x})={\sum }_{t=1}^T{h}_t(\mathbf{x})$

---

GBDT流程（分类）

GBDT用于分类仍然使用CART回归树，使用softmax进行概率的映射，然后对概率的残差进行拟合

1.针对每个类别都先训练一个回归书，如三个类别，训练三棵树。就是比如对于样本$x_i$为第二类，则输入三棵树分别为：（$x_i$，0），（$x_i$，1），（$x_i$，0）这其实是典型的OvR的多分类训练方式。而每棵树的训练过程就是CART的训练过程。这样，对于样本$x_i$就得出了三棵树的预测值$F_1(x_i)$，$F_2(x_i)$，$F_3(x_i)$，模仿多分类的逻辑回归，用softmax来产生概率，以类别1为例：$p_1\left({\mathbf{x}}_{\mathbf{i}}\right)=\exp \left(F_1\left({\mathbf{x}}_{\mathbf{i}}\right)\right)/{\sum }_{l=1}^3\exp \left(F_l\left({\mathbf{x}}_{\mathbf{i}}\right)\right)$

2.对每个类别分别计算残差，如类别1:${\tilde{y}}_{i1}=0-p_1\left({\mathbf{x}}_{\mathbf{i}}\right)$，类别2:${\tilde{y}}_{i2}=1-p_2\left({\mathbf{x}}_{\mathbf{i}}\right)$，类别3:${\tilde{y}}_{i3}=0-p_3\left({\mathbf{x}}_{\mathbf{i}}\right)$

3.开始第二轮的训练，针对第一类输入为$\left({\mathbf{x}}_{\mathbf{i}},{\tilde{y}}_{i1}\right)$,针对第二类输入为$\left({\mathbf{x}}_{\mathbf{i}},{\tilde{y}}_{i2}\right)$，针对第三类输入为$\left({\mathbf{x}}_{\mathbf{i}},{\tilde{y}}_{i3}\right)$，继续训练出三棵树。

4.重复3直到迭代M轮，就得到了最后的模型。预测的时候只要找出概率最高的即为对应的类别

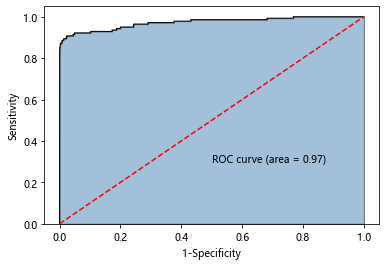
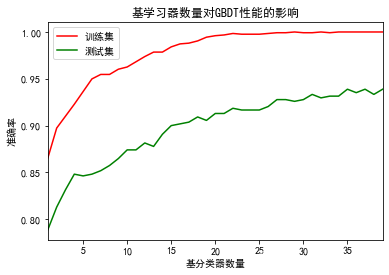
GBDT原理案例举例

import numpy as np
import matplotlib.pyplot as plt
#回归时分类的极限思想
#分类的类别多到一定程度，那么就是回归
from sklearn.ensemble import GradientBoostingClassifier,GradientBoostingRegressor
from sklearn import tree# X数据：购物金额和上网时间
# y目标：14（高一），16（高三），24（大学毕业），26（工作两年）
X = np.array([[800,3],[1200,1],[1800,4],[2500,2]])
y = np.array([14,16,24,26]) gbdt = GradientBoostingRegressor(n_estimators=10)
gbdt.fit(X,y)
gbdt.predict(X)
#array([16.09207064, 17.39471376, 22.60528624, 23.90792936])

第一颗决策树，根据平均值，计算了残差[-6,-4,4,6]

plt.rcParams["font.sans-serif"] = ["Heiti TC"]
plt.figure(figsize=(9,6))
_ = tree.plot_tree(gbdt[0,0],filled=True,feature_names=["消费","上网"])

#计算friedman_mse
((y-y.mean())**2).mean()
#26.0
((y[:2]-y[:2].mean())**2).mean()
#1.0

value（-6，-4，6，4）是14，16，26，24和20的差，即残差
残差越小——>越好——>越准确

第二颗决策树,根据梯度提升，减少残差（残差越小，结果越好，越准确）

plt.rcParams["font.sans-serif"] = ["Heiti TC"]
plt.figure(figsize=(9,6))
_ = tree.plot_tree(gbdt[1,0],filled=True,feature_names=["消费","上网"])

gbdt1 = np.array([-6,-4,6,4])
#梯度提升
gbdt2 = gbdt1 - gbdt1*0.1   #learning_rate = 0.1
#array([-5.4, -3.6,  5.4,  3.6])

第三颗决策树

plt.rcParams["font.sans-serif"] = ["Heiti TC"]
plt.figure(figsize=(9,6))
_ = tree.plot_tree(gbdt[0,0],filled=True,feature_names=["消费","上网"])

gbdt1 = np.array([-5.4,-3.6,5.4,3.6])
#梯度提升
gbdt1  - gbdt1 *0.1 #learning_rate = 0.1
#array([-4.86, -3.24,  4.86,  3.24])

最后一棵树

plt.rcParams["font.sans-serif"] = ["Heiti TC"]
plt.figure(figsize=(9,6))
_ = tree.plot_tree(gbdt[-1,0],filled=True,feature_names=["消费","上网"])

#learning_rate = 0.1
gbdt = np.array([-2.325,-1.55,1.55,2.325])
#梯度提升 学习率0.1
residual = gbdt - gbdt*0.1
residual
#array([-2.0925, -1.395 ,  1.395 ,  2.0925])y - residual
#array([16.0925, 17.395 , 22.605 , 23.9075])
gbdt.predict(X)
#array([16.09207064, 17.39471376, 22.60528624, 23.90792936])

根据最后一棵树的残差，计算了算法最终的预测值
直接使用算法predict返回的值和手算一模一样