安全多方计算之GMW协议

article/2025/9/13 22:28:23

安全多方计算之GMW协议

一、背景

论文原文《How to play any mental game》。作者：Micali S, Goldreich O, Wigderson A. 发表在：Proceedings of the Nineteenth ACM Symp on Theory of Computing, STOC.

GMW协议可以同时适用在布尔电路和算术电路，支持n个参与方参与计算。GMW协议基于秘密共享技术对电路中的导线进行秘密共享。

二、背景技术

XOR秘密共享属于（n,n）门限秘密共享。假设一个秘密值为s，则选择n-1个同比特长的随机数 $r_1,r_2,...r_{n-1}$ ,计算 $r_n=s\bigoplus r_1\bigoplus r_2\bigoplus ...\bigoplus r_{n-1}$ 。 $r_1$ 到 $r_n$ 就是秘密值的分享。恢复秘密值s只需计算 $s=r_1\bigoplus r_2\bigoplus ...\bigoplus r_n$ 即可。

1-out-of-4 OT协议，参与方之间需要执行4选1OT协议，接收方从四个密文中选择需要的密文，而发送方不知道接收方选择了哪一个密文。

三、协议内容

GMW可以对三种运算——NOT，XOR和AND运算进行evaluate。

两个数据持有方对数据a，b进行比特级秘密共享： $a=a_1\bigoplus a_2\bigoplus ...\bigoplus a_n$ ， $b=b_1\bigoplus b_2\bigoplus ...\bigoplus b_n$ 。将 $a_i$ , $b_i$ 分别发送给计算方 $P_i$ 。

对于NOT和XOR运算，每个计算方 $P_i$ 只需在本地进行计算即可。NOT运算输出的分享值为： $c_i=!a_i$ ；XOR运算输出的分享值为： $c_i=a_i\bigoplus b_i$ 。

对于AND运算则需要两两计算方进行交互。计算：

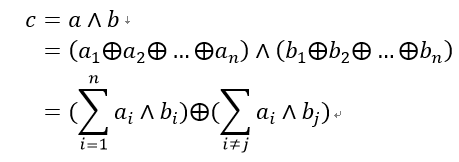
注意：这里的求和符号代表的是异或求和。根据上述公式，每一个计算方可以在本地计算 $\sum ^{n}_{i=1}{a_i\wedge b_i}$ 。然后对于任意两个计算方 $P_i$ ， $P_j$ ，需要交互计算： $(a_i\wedge b_j)\bigoplus (a_j\wedge b_i)$ 。此时 $P_i$ ， $P_j$ 需要执行一个1-out-of-4 OT协议：

假设 $P_i$ 为OT协议发送方， $P_j$ 为OT协议接收方。定义函数S：

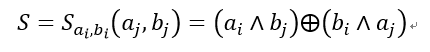
$P_i$ 选择一个随机数r，然后计算一个OT协议的秘密表:

于是，AND运算的结果 $c=c_1\bigoplus c_2\bigoplus ...\bigoplus c_n$ 。 $P_j$ 根据自己的秘密分享值选择表中相应的值作为自己的输出秘密分享值，保留r作为自己的输出秘密分享值。这样，在这一小轮中，得到的秘密分享值为r，得到的秘密分享值为。每个计算方两两交互后将得到的所有的值进行异或求和就可以得到 $\sum_{i\neq j}{a_i\wedge b_j}$ 的值。然后每一个计算方 $P_i$ 就可以得到自己的秘密份额： $c_i=(a_i\wedge b_i)\bigoplus (\sum_{i\neq j}{a_i\wedge b_j})$ 。