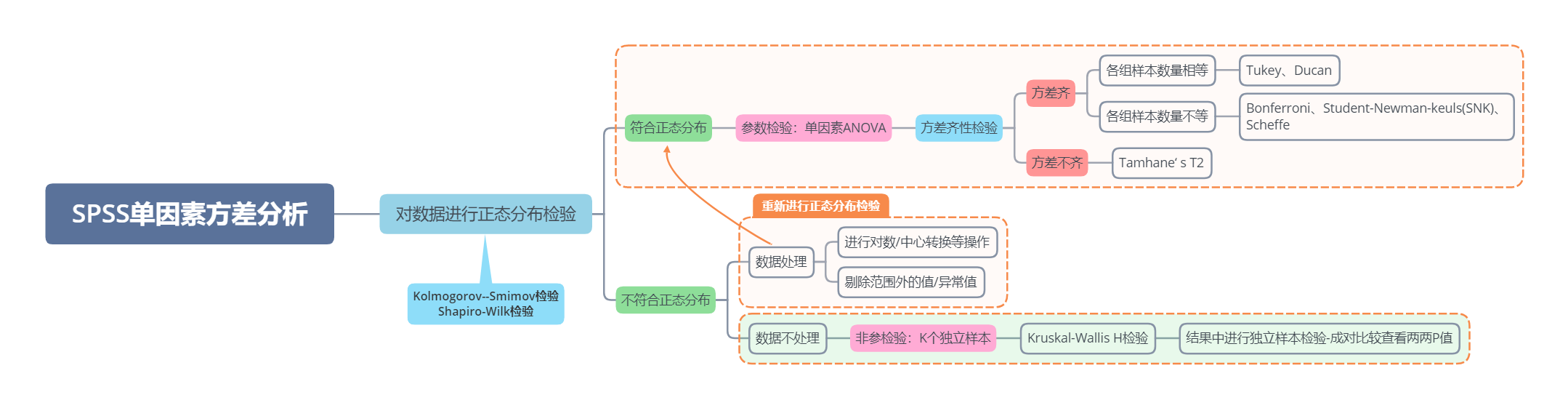
前言:本文为个人学习笔记,为各大网站上的教学内容之综合整理,综合整理了①方差分析的基础知识、②方差分析(单因素方差分析、双因素方差分析)在Excel、SPSS、R语言中的操作),尽量标明出处。另因能力所限或有纰漏之处,故仅供参考,欢迎交流指正。
基础知识
基本概念
指标:研究对象的某种特征指标
因子:影响指标的各种因素
水平:一般将因子控制在几个不同的状态上,每个状态称为因子的一个水平
单因素试验:试验中只改变一个因子的水平,其他因子保持不变
多因素试验:试验中改变多个因子的水平
方差检验前提假设
正态性:每组样本数据对应的总体应该服从正态分布
方差齐性:每组样本数据对应的总体方差相等
独立性:每组之间的值是相互独立的
方差检验步骤
1.建立假设
:
:样本组的均值不全相等
2.确定检验水准
检验水准,指本来成立,却根据样本信息拒绝
的可能性大小。即拒绝
时最大允许误差的概率,常用0.05。
3.计算各统计量,求出F值
假设研究因子A有s个水平,每个水平下样本数量分别为,
,……,
对每个水平下的样本
,
,……,
,引进统计量
水平下样本和:
水平 下样本均值:
样本总均值:
偏差平方和及其分解
总平方和:
组间平方和:
组内平方和:
平方和分解公式:
平方和化简公式
| 误差来源 | 平方和 | 自由度 | 均方 | F值 | 临界值 |
|---|---|---|---|---|---|
| 因子A | s-1 | ||||
| 随机误差 | n-s | ||||
| 总和 | n-1 |
该统计量应当服从F分布,从而可以计算出P值。
4.得出结论
按照事先确定的界定P值对进行取舍,作出推断结论,引申出实用性结论。
若P≤,
认为出现了小概率事件,拒绝接受
。可以认为样本与总体的差异存在本质区别,而非偶然,这种差别有统计学意义。
若P>,
认为出现了常见事件,不拒绝。可以认为样本与总体的差异不存在本质区别,可能存在偶然,两者差别无统计学意义。
主效应
在有一个或几个因子的多水平的实验中,描述一个因子在各水平上对反应量影响大小的度量。对有S个水平的单因子A的试验,若随机变量 yij是在第 j次试验中于第 i个水平上的观测值,则模型为E(yij)=μ+ai,(i=1,2,...,s,j=1,2,...,ni),这里E是期望, μ是总平均, ai即A因子第 i个水平的主效应。
交互效应
当被试处理情境之间或单元之间的平均数差异显著不同于因素的全部主效应时,双因素之间的交互作用就发生了。或者可以这样理解,当双因素实验研究的结果以图形呈现的时候,如果存在不平行的折线,则说明存在交互作用。
交互效应显著的几种情况, 列出了6种类型
自变量的主效应与交互效应存在关联性,需要具体情况具体分析。当交互效应不显著时,两个自变量相互独立,可直接由主效应是否显著来评估自变量对因变量的作用大小。当交互效应显著时,不能简单从主效应是否显著得出结论。
以交互效应显著为前提,来区分自变量A的主效应是否显著的三种情况:
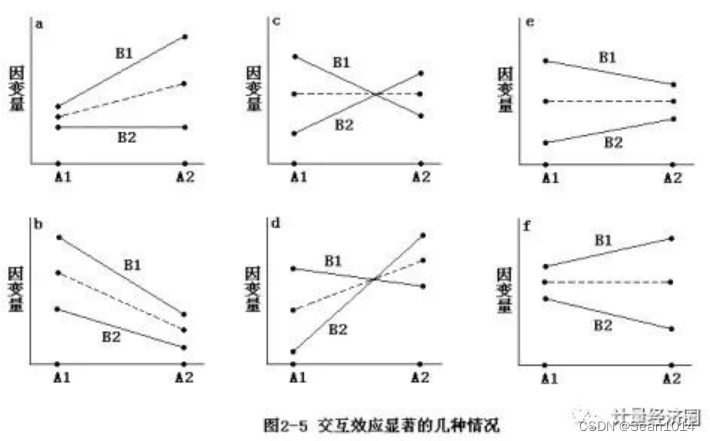
第一,交互效应显著,A的主效应也显著,而且主效应方向与简单效应方向一致(图b)。这种情况下,在自变量B的两个水平上,自变量A从A1到A2的变化引起的因变量的变化趋势一致,只是变化幅度不一致。这里的交互效应掩盖了自变量A在自变量B不同水平上的效应量的差异。很明显,在B1上平上,A的效应量大于其在B2水平上的效应量。
第二,交互效应显著,A的主效应也显著,这时A的效应方向可能会被交互效应歪曲(图a、d)。在图a中,A的变化在B1的水平上引起了因变量的显著变化,但在B2水平上却未引起因变量的变化,这就是说A的变化不是在任何情况下都会引起因变量的变化的,它依赖于自变量B的水平;在图d中,虽然A的变化在B的两个水平上都引起了因变量的明显变化,但是变化的方向正好相反,从其主效应看,A的水平提高可以促进因变量分数的提高,但实际情况是,当A在B1水平上提高时,反而会导致因变量分数的下降。所以在这种情况下,显著的交互效应掩盖或歪曲了自变量A的作用机制,它在B的不同水平上效应量是不同的。
第三,交互效应显著,A的主效应却不显著,实际上是交互效应掩盖了A的效应(图c、e、f)。我们从这些图示中可以明显看到A的效应,但方差分析结果却会显示A的主效应不显著,这是因为A在B的两个水平上的效应方向相反,计算A的主效应时A1和A2的差异量被掩盖在了平均过程中。
那么,如何依据自变量主效应和其与其它自变量的交互效应来进行结果分析呢?这一点很简单:当方差分析结果显示A的主效应及A与其它自变量的交互效应都不显著时,则说明A的效应真的不明显;当方差分析的结果显示A的主效应不显著但A与其它自变量的交互效应显著时,则说明A其实是对因变量有明显作用的,即A的效应其实是存在的,只不过其效应的大小和方向依赖于其它自变量的不同水平。
上述分析提醒我们,在说明方差分析结果时你要特别注意,如果因子间的交互效应达到了显著性水平,那么自变量的效应有可能会被歪曲或掩盖,也就是说,不能简单地依据其主效应是否显著来判断它是否对因变量有影响,而是要进行简单效应检验,分别考察其在其它自变量不同水平上的变化情况。否则,可能会得到错误结论。应该记住,一个因子的主效应是对其在另外一个因子所有不同水平下观测分数的平均而得到的,而这种平均的结果可能很难准确地反映每种具体实验处理的效应。
单因素方差分析
例1:对某年级三个班进行抽查,随机抽取了来自1、2、3班的同学,已知1班4名同学的成绩分别为37、47、40、60,2班6名同学的成绩分别为60、86、67、92、95、98,3班3名同学的成绩分别为69、100、98,设各班成绩方差齐性正态分布,问这三个班同学成绩有无显著差异?(显著性水平0.05)
Excel
将数据按列录入表格
方法1:按照原本的公式计算

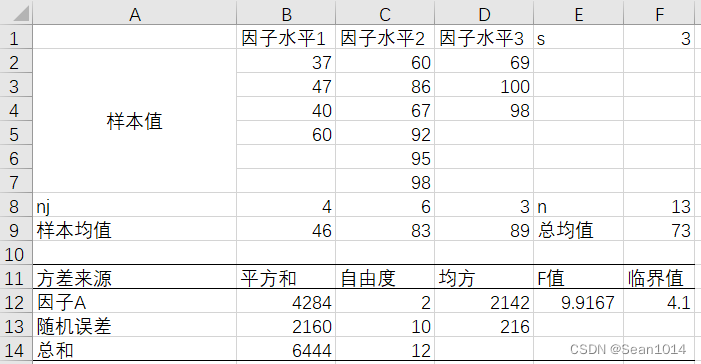
9.9167>4.10,F值大于临界值,拒绝接受
,认为三个班成绩不全相等。
方法2:按照化简的公式计算
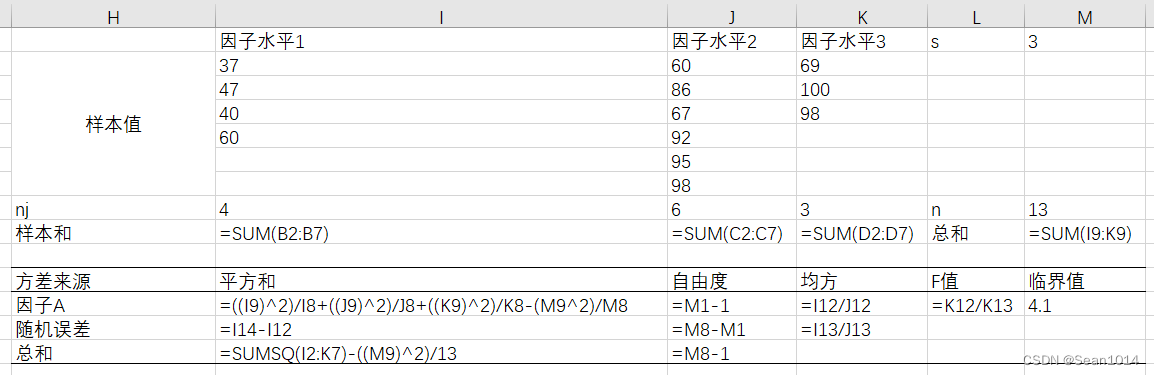
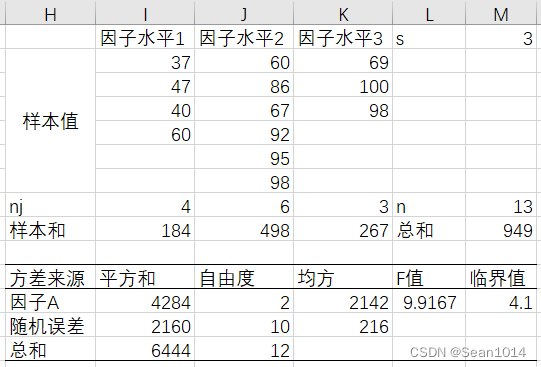
9.9167>4.10,F值大于临界值,拒绝接受
,认为三个班成绩不全相等。
*方法1、2中计算随机误差是采用差值法求得,可以用以下两种方法验算
方法1:按照原本的公式计算(第18行)
方法2:用内置函数VAR.P计算(第19行)

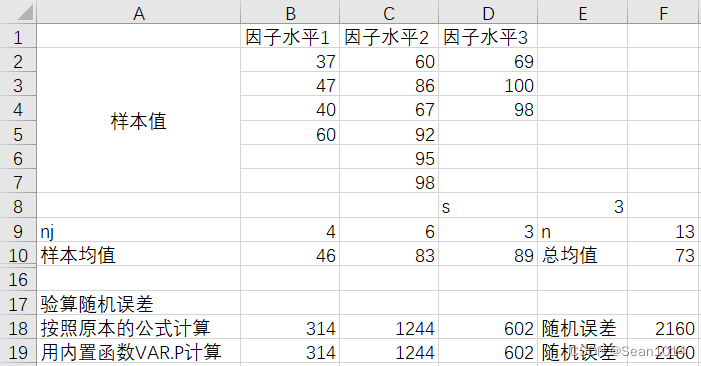
验算求得为2160,与差值法结果相等。
方法3:数据分析工具
【操作】数据-分析-数据分析-方差分析:单因素方差分析
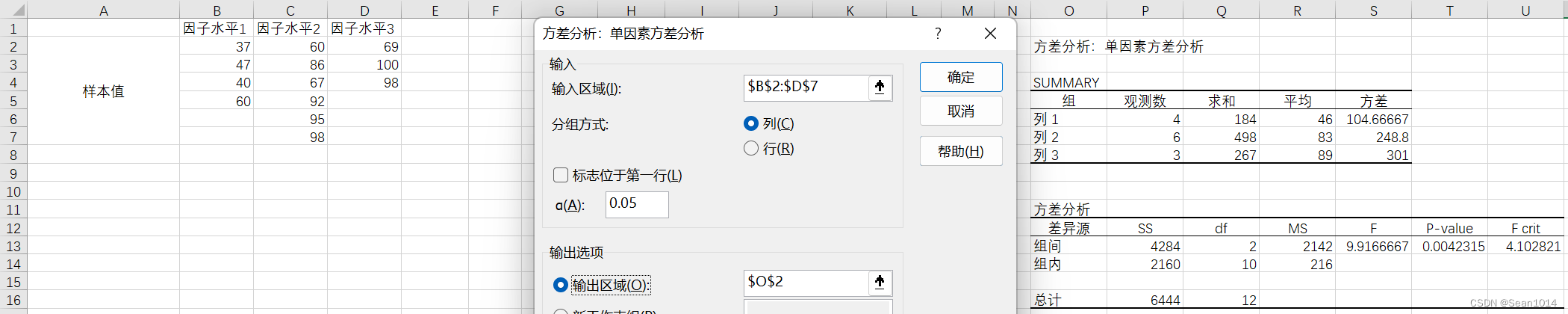
9.9167>4.10,F值大于临界值,拒绝接受
,认为三个班成绩不全相等。
SPSS
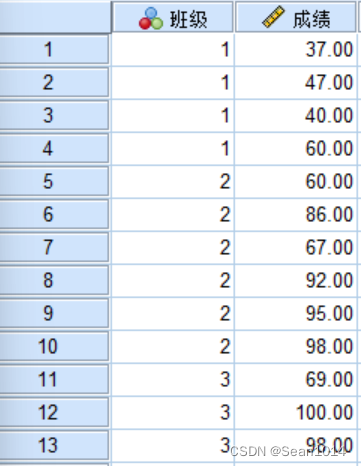
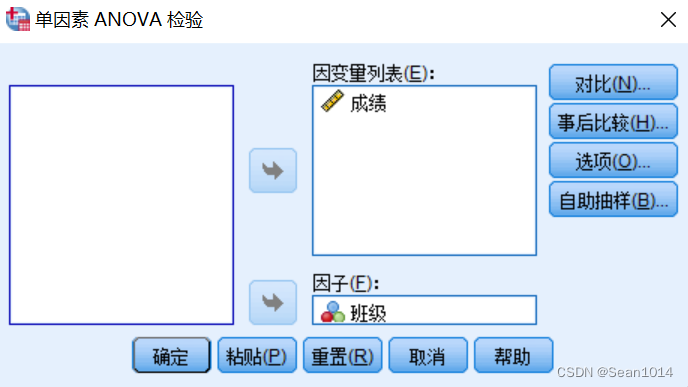
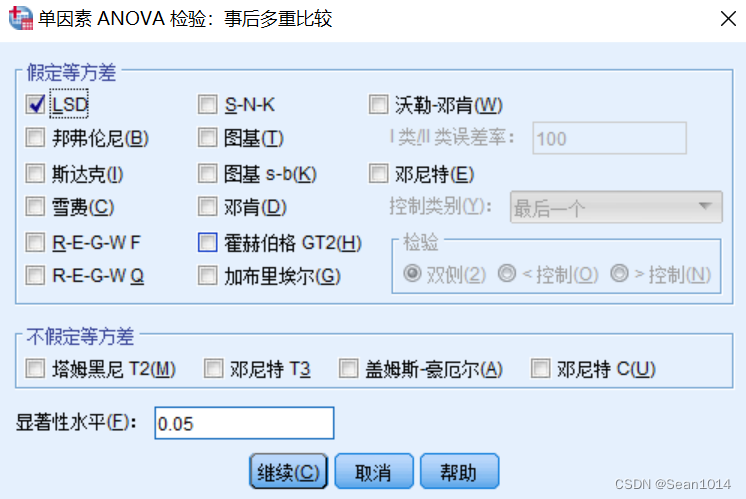
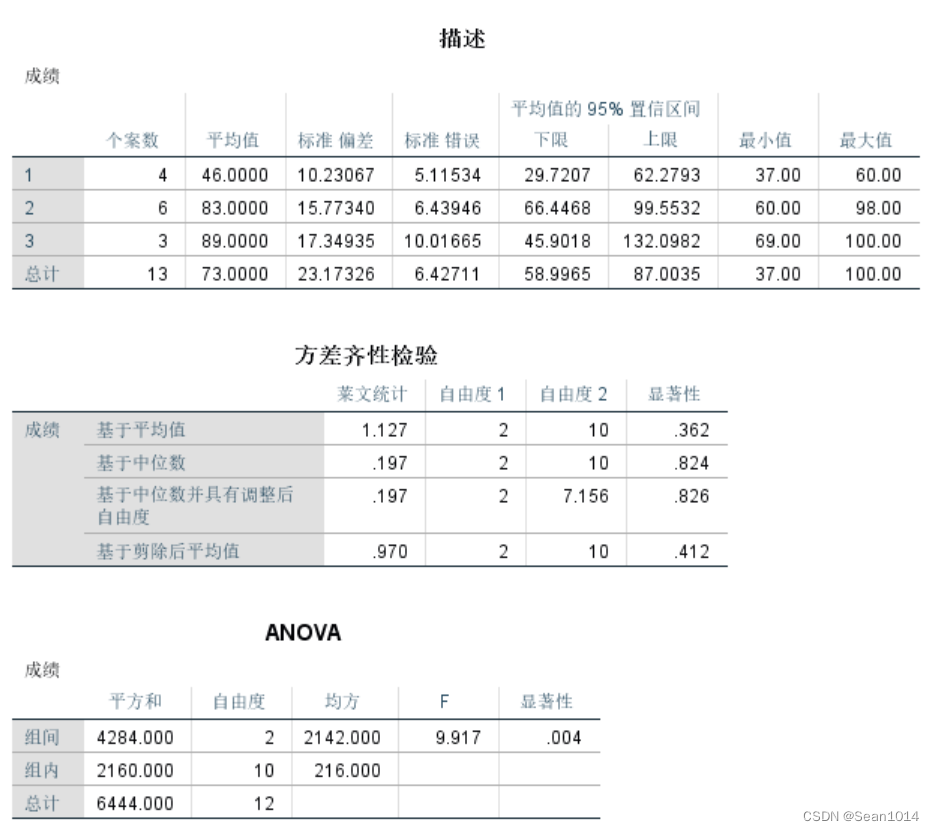
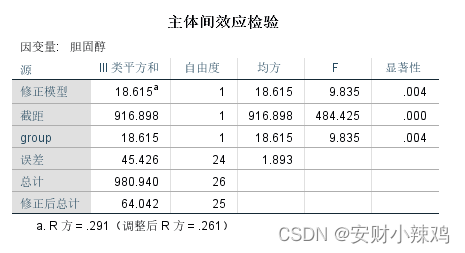
9.9167>4.10,F值大于临界值,拒绝接受
,认为三个班成绩不全相等。
多重比较
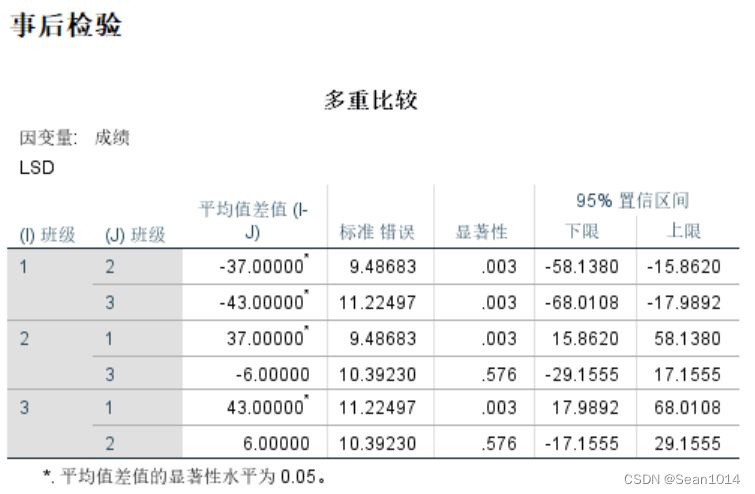
1与2、3有显著差异,2与3无显著差异。
R语言
参考资料:
R语言基础数据分析—单因素方差分析_吹哨子的喇叭花的博客-CSDN博客_r语言单因素方差分析
【R-数据科学】方差分析(ANOVA)在R语言中如何实现?(附数据和代码) - 知乎
X1<-c(37,47,40,60,60,86,67,92,95,98,69,100,98) # 录入指标的值
Fac<-factor(c(rep(1,4),rep(2,6),rep(3,3))) # 录入因子的值
df<-data.frame(X1,Fac) # 建立数据框
df.aov<-aov(X1~Fac,df) # 用aov()函数进行方差分析
summary(df.aov) # 用summary()函数提取方差分析的信息结果如下

Df表示自由度,Sum Sq表示平方和,Mean Sq表示均方,F value是F值,Pr(>F)是P值。9.9167>4.10,F值大于临界值,P<0.01,拒绝接受
,认为三个班成绩不全相等。
多重比较(LSD法和Duncan法)
install.packages("agricolae") # 安装agricolae包
library(agricolae) # 加载agricolae包
# 进行LSD法多重比较,bonferroni对P值进行修正
df.lsd<-LSD.test(df.aov,'Fac',p.adj = 'bonferroni')
print(df.lsd$groups) # 输出多重比较结果LSD法多重比较结果:

df.duncan<-duncan.test(df.aov,'Fac') # 进行Duncan法多重比较
print(df.duncan$groups) # 输出多重比较结果Duncan法多重比较结果:

双因素方差分析
多因素方差分析_俊红的数据分析之路的博客-CSDN博客_多因素方差分析
例2:假设A因子有5个水平,B因子有4个水平,两因子间不存在交互作用。观测值无重复,试进行双因素方差分析。(无重复双因素分析)
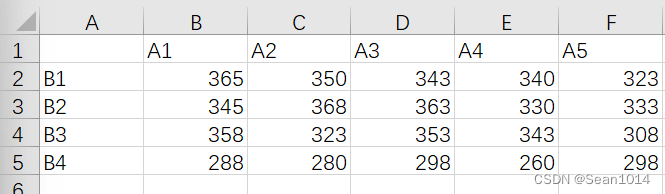
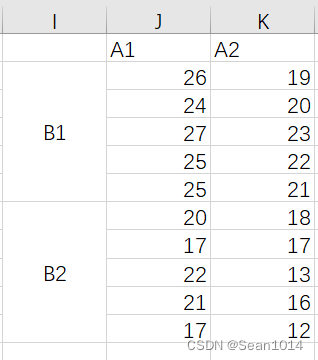
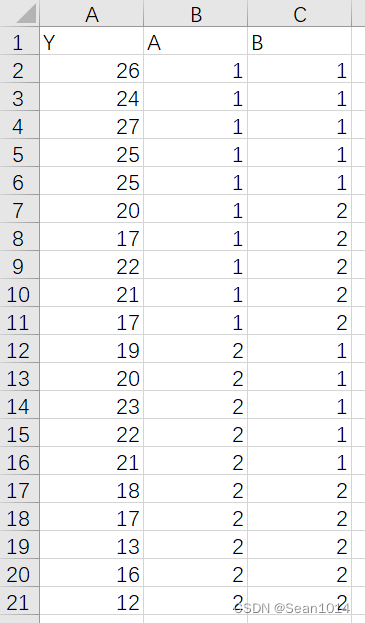
例3:假设A因子有2个水平,B因子有2个水平,两因子间存在交互作用。每组观测值有5个重复,试进行双因素方差分析。(可重复双因素分析)
Excel
不存在交互作用(例2)
数据-分析-数据分析-方差分析:无重复双因素分析
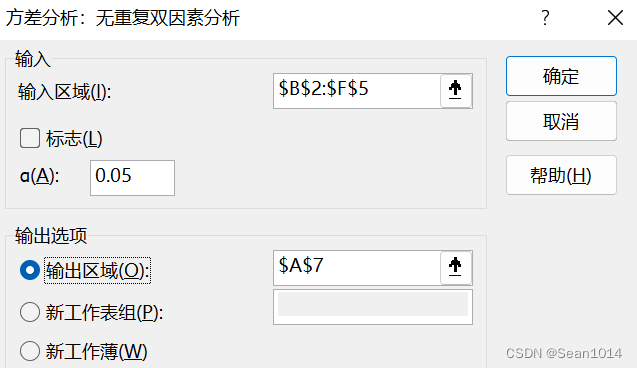
结果如下
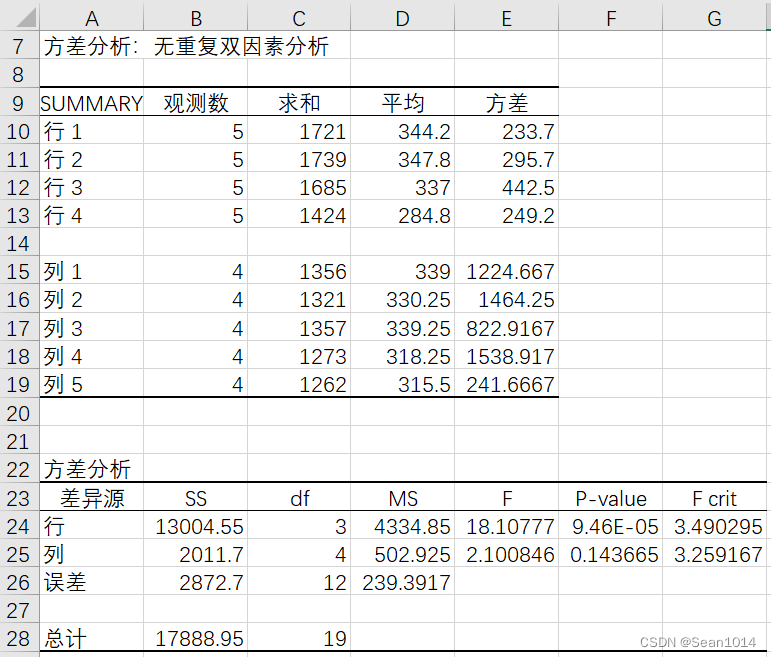
行P值<0.05,说明B因子之间差异显著,列P值>0.05,说明A因子之间差异不显著。
存在交互作用(例3)
数据-分析-数据分析-方差分析:可重复双因素分析
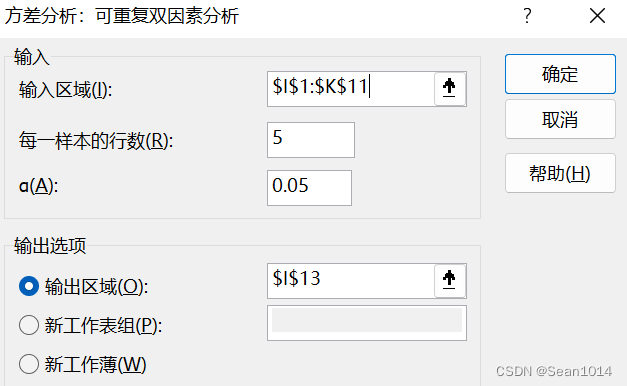
结果如下
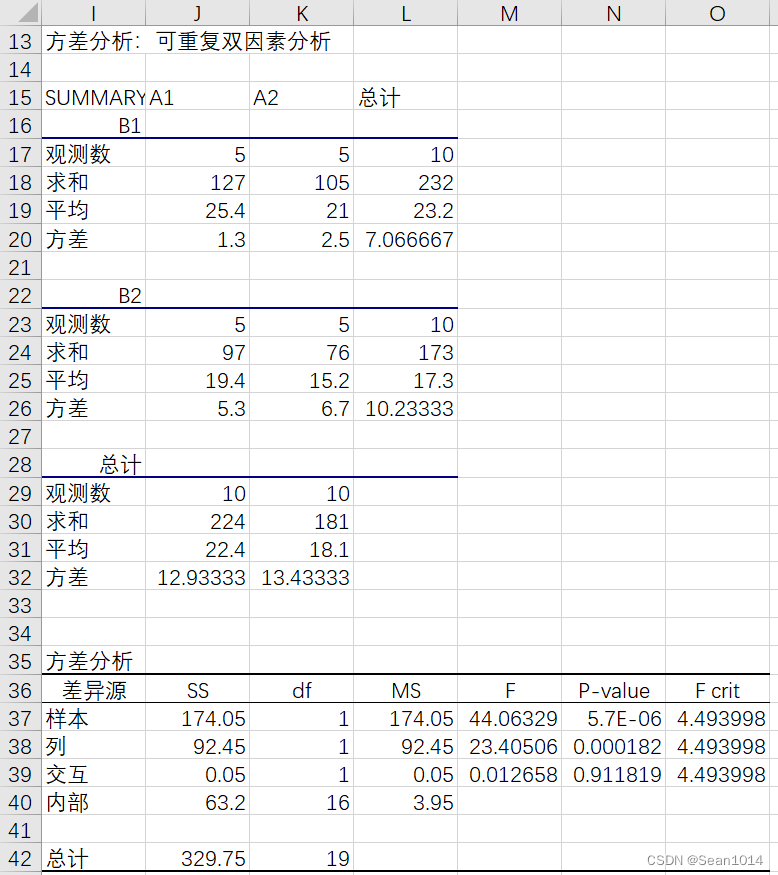
样本P值<0.05,说明B因子之间差异显著,列P值<0.05,说明A因子之间差异显著,交互P值>0.05,说明交互作用对观测量无显著影响。
*注意例2和例3在选择“输入区域”时,前者不框选非数值区域,后者需要框选数值区域,即需要框选A、B因子。
SPSS
不存在交互作用(例2)
SPSS方差分析两因素无交互项 - 百度文库
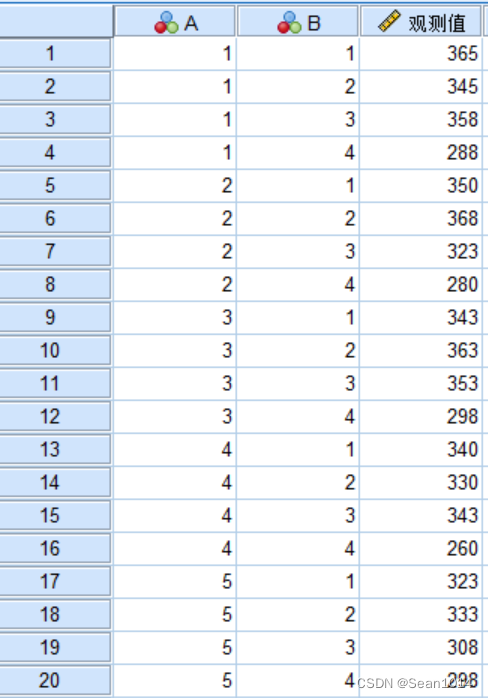

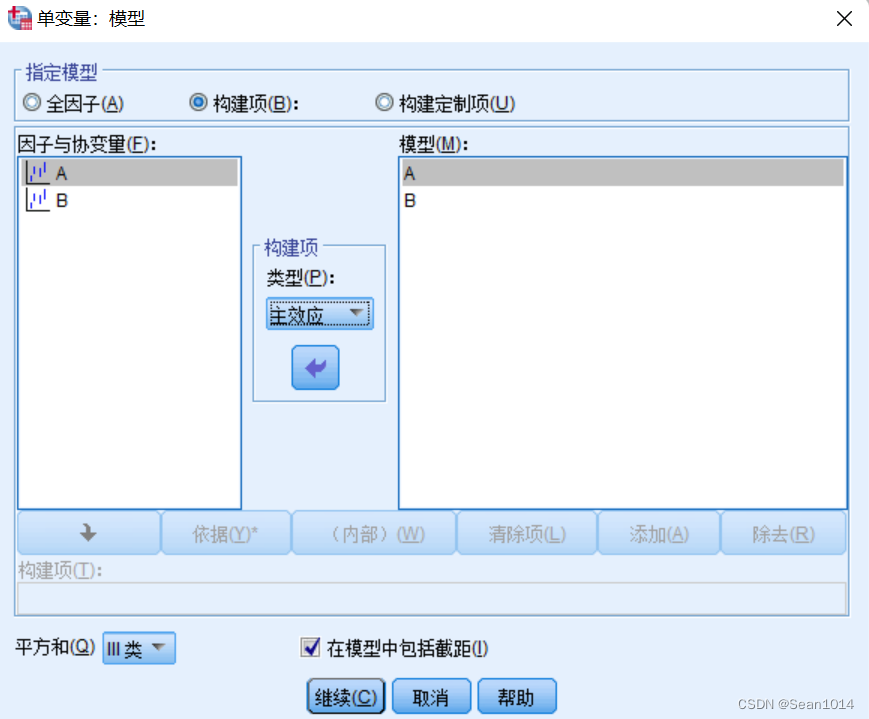
将两个因子加入模型中
确定,主体间效应检验结果如下:
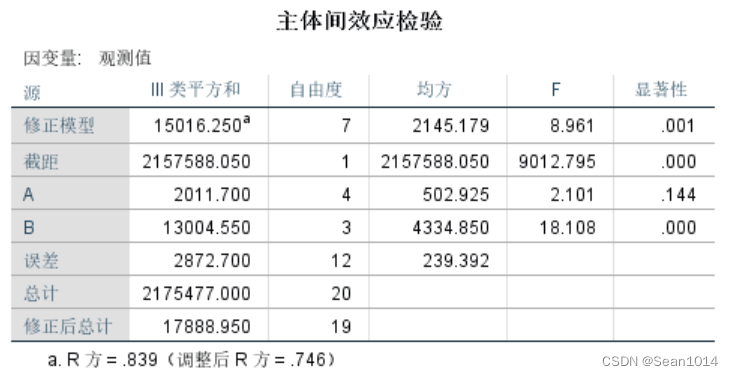
与Excel法对比过程量的值均相同。行P值<0.05,说明B因子之间差异显著,列P值>0.05,说明A因子之间差异不显著。
事后检验结果如下:
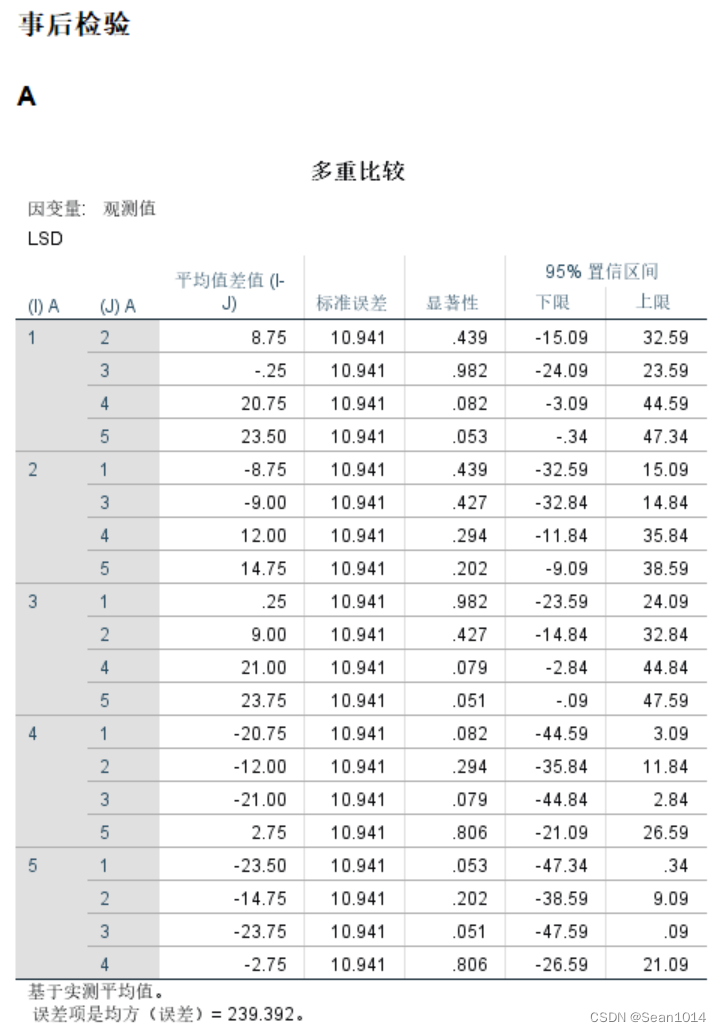
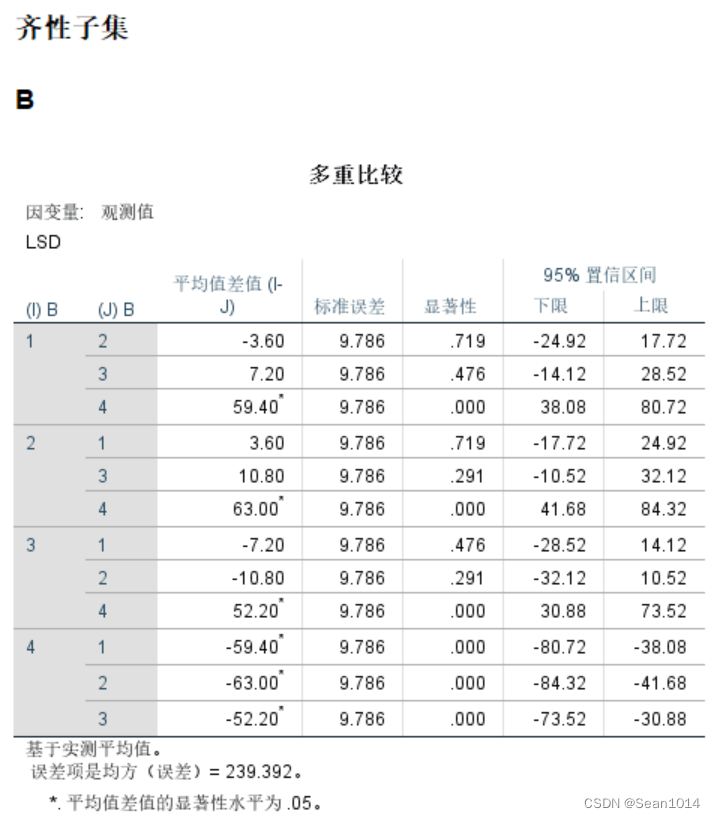
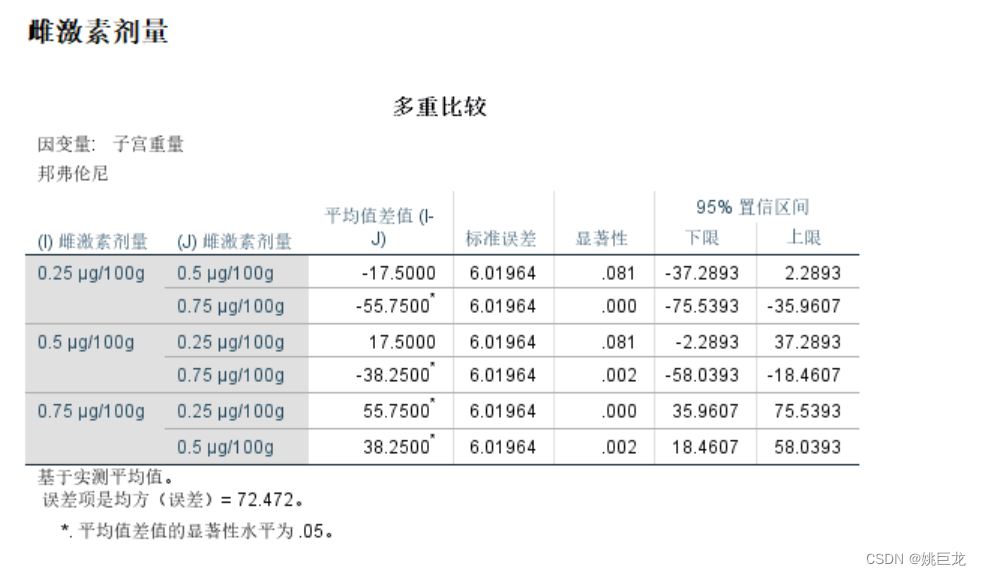
A因子的多重比较中不带有*号,B因子的多重比较结果说明B4与B1、B2、B3均存在显著差异,而B1、B2、B3之间不存在显著差异。
存在交互作用(例3)
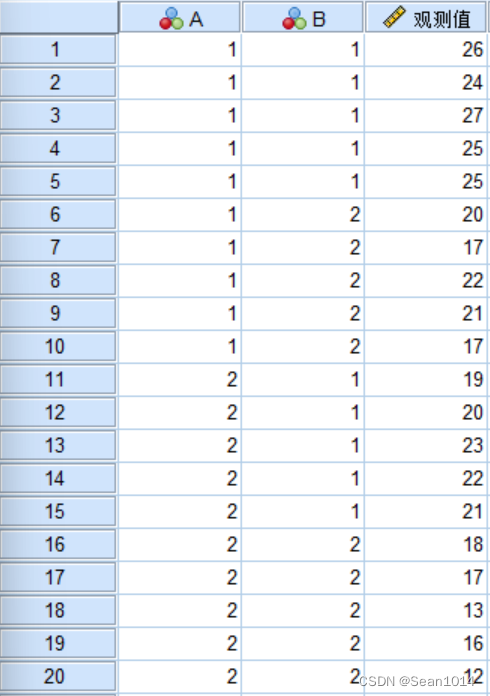


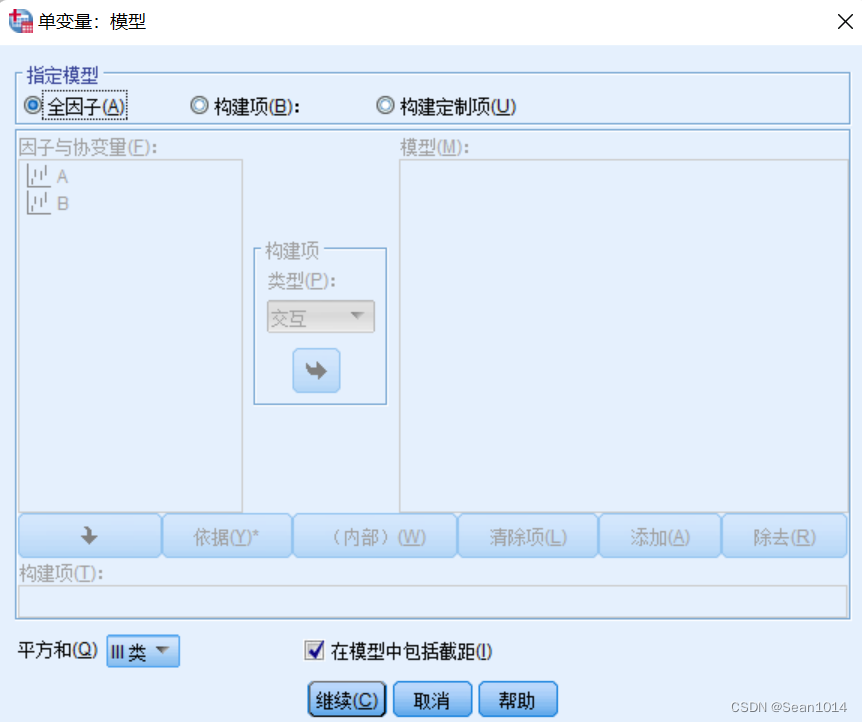
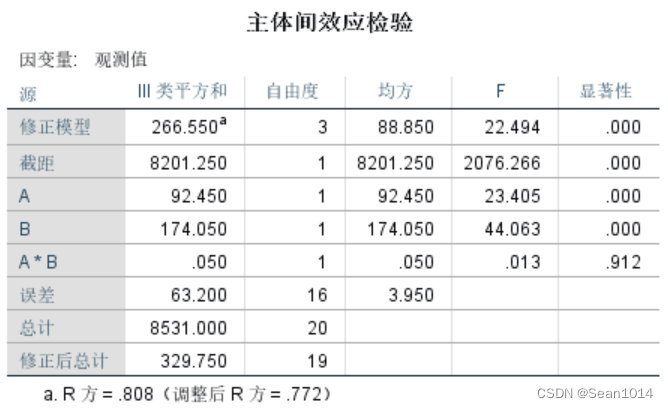
确定,主体间效应结果如下:
与Excel法对比过程量的值均相同。A、B因子显著性均小于0.05,说明A、B因子内差异显著,交互P值0.912>0.05,说明交互作用对观测量无显著影响。
R语言
不存在交互作用(例2)
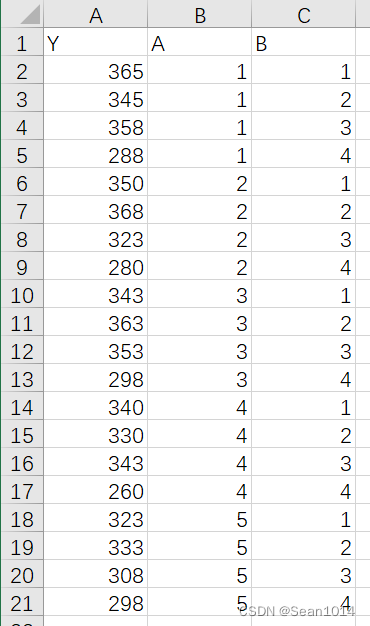
# 将excel中的数据导入data1
library(readxl)
data1<-read_excel('D:/D-WORK/R语言练习/data1.xlsx',"Sheet1")
# 将数值型的变量转化为因子型
data1$A<- factor(data1$A,levels = c(1:5),labels = c("A1","A2","A3","A4","A5") )
data1$B<- factor(data1$B,levels = c(1:4),labels = c("B1","B2","B3","B4") )
# 进行双因素方差分析
aov_data1<-aov(Y~A+B, data=data1)
# 查看结果
aov_data1
summary(aov_data1)结果如下:
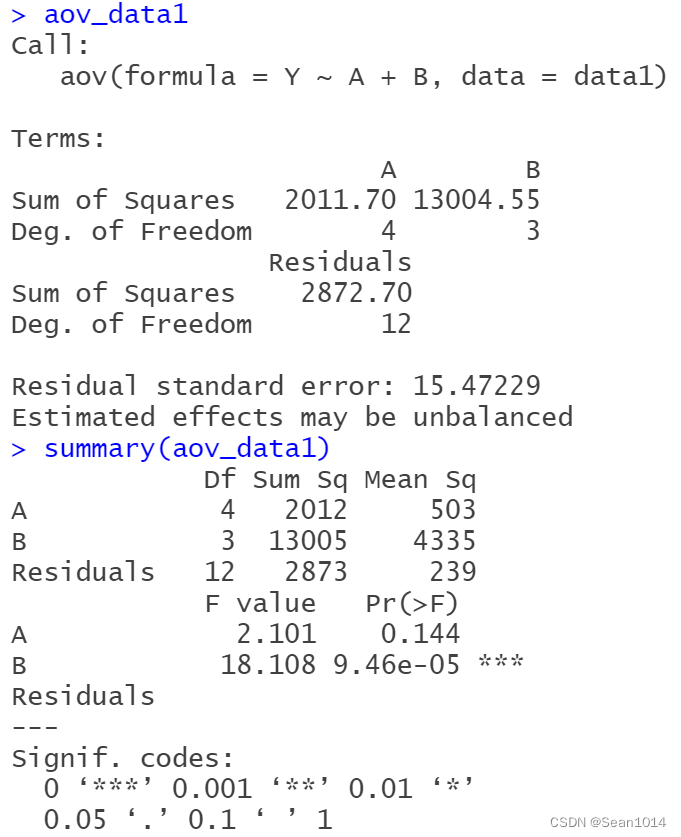
与Excel法、SPSS法对比过程量的值均相同。结果中B这行P值<0.0001,同时自动标注了***的显著程度,可见B因子之间在0.01%水平上差异显著,A这行P值>0.05,没有任何标注,说明A因子之间差异不显著。
存在交互作用(例3)
# 将excel中的数据导入data2
library(readxl)
data2<-read_excel('D:/D-WORK/R语言练习/data1.xlsx',"Sheet2")
# 将数值型的变量转化为因子型
data2$A<- factor(data2$A,levels = c(1:2),labels = c("A1","A2") )
data2$B<- factor(data2$B,levels = c(1:2),labels = c("B1","B2") )
# 进行双因素方差分析
aov_data2<-aov(Y~A*B, data=data2)
# 查看结果
aov_data2
summary(aov_data2)结果如下:

与Excel法、SPSS法对比过程量的值均相同。结果中B这行P值<0.0001,同时自动标注了***的显著程度,可见B因子之间在0.01%水平上差异显著,A这行P值>0.05,没有任何标注,说明A因子之间差异不显著。
aov函数表达式
R语言_方差分析_Young_Gy的博客-CSDN博客_r语言三因素方差分析
R语言完成双因素方差分析的简单小例子_哔哩哔哩_bilibili
多重比较
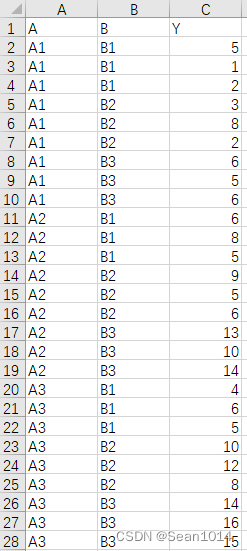
例4:假设A因子有3个水平,B因子有3个水平,观测值有3个重复,两因子间不清楚是否存在交互作用。试进行双因素方差分析并进行多重比较。
实践:spss双因素方差分析及图表制作_哔哩哔哩_bilibili
这个视频中有详细的SPSS方法步骤。关键在数据-选择个案-设置条件。
用R实现代码如下:
进行多重比较时分为①A因素相同B因素不同②B因素相同A因素不同,来进行
# 导入数据,AB列转换为因子型,进行含交互作用的方差分析,输出结果
library(readxl)
data4<-read_excel('D:/r语言/data1.xlsx',"Sheet4",range = "A1:C28")
data4$A<- factor(data4$A,levels = c("A1","A2","A3"),labels = c("A1","A2","A3") )
data4$B<- factor(data4$B,levels = c("B1","B2","B3"),labels = c("B1","B2","B3") )
aov_data4<-aov(Y~A*B, data=data4)
summary(aov_data4)#A因素相同B因素不同进行多重比较
library(agricolae)
data4_A1<-data4[c(1:9),]
aov_data4_A1<-aov(Y~B, data=data4_A1)
summary(aov_data4_A1)
duncan_data4_A1<-duncan.test(aov_data4_A1,'B')
print(duncan_data4_A1$groups)data4_A2<-data4[c(10:18),]
aov_data4_A2<-aov(Y~B, data=data4_A2)
summary(aov_data4_A2)
duncan_data4_A2<-duncan.test(aov_data4_A2,'B')
print(duncan_data4_A2$groups)data4_A3<-data4[c(19:27),]
aov_data4_A3<-aov(Y~B, data=data4_A3)
summary(aov_data4_A3)
duncan_data4_A3<-duncan.test(aov_data4_A3,'B')
print(duncan_data4_A3$groups)#B因素相同A因素不同进行多重比较
data4_B1<-data4[c(1:3,10:12,19:21),]
aov_data4_B1<-aov(Y~A, data=data4_B1)
summary(aov_data4_B1)
duncan_data4_B1<-duncan.test(aov_data4_B1,'A')
print(duncan_data4_B1$groups)data4_B2<-data4[c(4:6,13:15,22:24),]
aov_data4_B2<-aov(Y~A, data=data4_B2)
summary(aov_data4_B2)
duncan_data4_B2<-duncan.test(aov_data4_B2,'A')
print(duncan_data4_B2$groups)data4_B3<-data4[c(7:9,16:18,25:27),]
aov_data4_B3<-aov(Y~A, data=data4_B3)
summary(aov_data4_B3)
duncan_data4_B3<-duncan.test(aov_data4_B3,'A')
print(duncan_data4_B3$groups)结果如下:
> summary(aov_data4)Df Sum Sq Mean Sq F value Pr(>F)
A 2 160.89 80.44 22.625 1.22e-05 ***
B 2 184.67 92.33 25.969 4.96e-06 ***
A:B 4 47.11 11.78 3.312 0.0336 *
Residuals 18 64.00 3.56
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1> summary(aov_data4_A1)Df Sum Sq Mean Sq F value Pr(>F)
B 2 13.56 6.778 1.356 0.327
Residuals 6 30.00 5.000
> print(duncan_data4_A1$groups)Y groups
B3 5.666667 a
B2 4.333333 a
B1 2.666667 a> summary(aov_data4_A2)Df Sum Sq Mean Sq F value Pr(>F)
B 2 68.22 34.11 9.303 0.0145 *
Residuals 6 22.00 3.67
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> print(duncan_data4_A2$groups)Y groups
B3 12.333333 a
B2 6.666667 b
B1 6.333333 b> summary(aov_data4_A3)Df Sum Sq Mean Sq F value Pr(>F)
B 2 150 75 37.5 0.000406 ***
Residuals 6 12 2
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> print(duncan_data4_A3$groups)Y groups
B3 15 a
B2 10 b
B1 5 c> summary(aov_data4_B1)Df Sum Sq Mean Sq F value Pr(>F)
A 2 20.67 10.333 4.043 0.0773 .
Residuals 6 15.33 2.556
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> print(duncan_data4_B1$groups)Y groups
A2 6.333333 a
A3 5.000000 ab
A1 2.666667 b> summary(aov_data4_B2)Df Sum Sq Mean Sq F value Pr(>F)
A 2 48.67 24.333 3.911 0.0818 .
Residuals 6 37.33 6.222
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> print(duncan_data4_B2$groups)Y groups
A3 10.000000 a
A2 6.666667 ab
A1 4.333333 b> summary(aov_data4_B3)Df Sum Sq Mean Sq F value Pr(>F)
A 2 138.67 69.33 36.71 0.000431 ***
Residuals 6 11.33 1.89
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> print(duncan_data4_B3$groups)Y groups
A3 15.000000 a
A2 12.333333 a
A1 5.666667 b