卷积是一种计算方法
1、一维连续卷积
1.1 基本概念
h ( x ) = f ( x ) ⊗ g ( x ) = ∫ − ∞ ∞ f ( u ) × g ( x − u ) d u h(x) = f(x)\otimes g(x) = \int_{-\infty}^{\infty}f(u)\times g(x-u)du h(x)=f(x)⊗g(x)=∫−∞∞f(u)×g(x−u)du
对于线性时不变系统,它的零状态响应可以通过系统的冲激响应h(t)与e(t)的卷积积分求得:
f ( t ) = ∫ − ∞ ∞ e ( τ ) × h ( t − τ ) d τ f(t) = \int_{-\infty}^{\infty}e(\tau)\times h(t-\tau) d\tau f(t)=∫−∞∞e(τ)×h(t−τ)dτ
对于这个理解,此网址由https://blog.csdn.net/palet/article/details/88862647很好的解释,下面主要引用此博客下的内容:
1.2 示例图解:
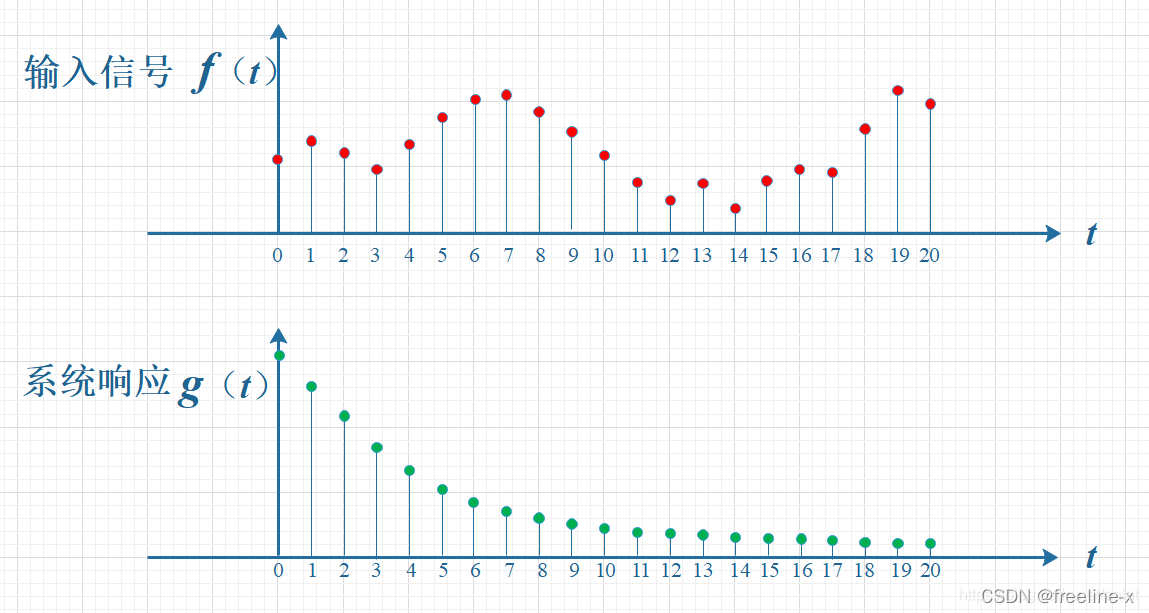
输入信号是 f(t) ,是随时间变化的。系统响应函数是 g(t) ,图中的响应函数是随时间指数下降的.如果在 t=0 的时刻有一个输入,那么随着时间的流逝,这个输入将不断衰减。换言之,到了 t=T时刻,原来在 t=0 时刻的输入f(0)的值将衰减为f(0)g(T)。
考虑到信号是连续输入的,也就是说,每个时刻都有新的信号进来,所以,最终输出的是所有之前输入信号的累积效果。如下图所示,在T=10时刻,输出结果跟图中带标记的区域整体有关。其中,f(10)因为是刚输入的,所以其输出结果应该是f(10)g(0),而时刻t=9的输入f(9),只经过了1个时间单位的衰减,所以产生的输出应该是 f(9)g(1),如此类推,即图中虚线所描述的关系。这些对应点相乘然后累加,就是T=10时刻的输出信号值,这个结果也是f和g两个函数在T=10时刻的卷积值。
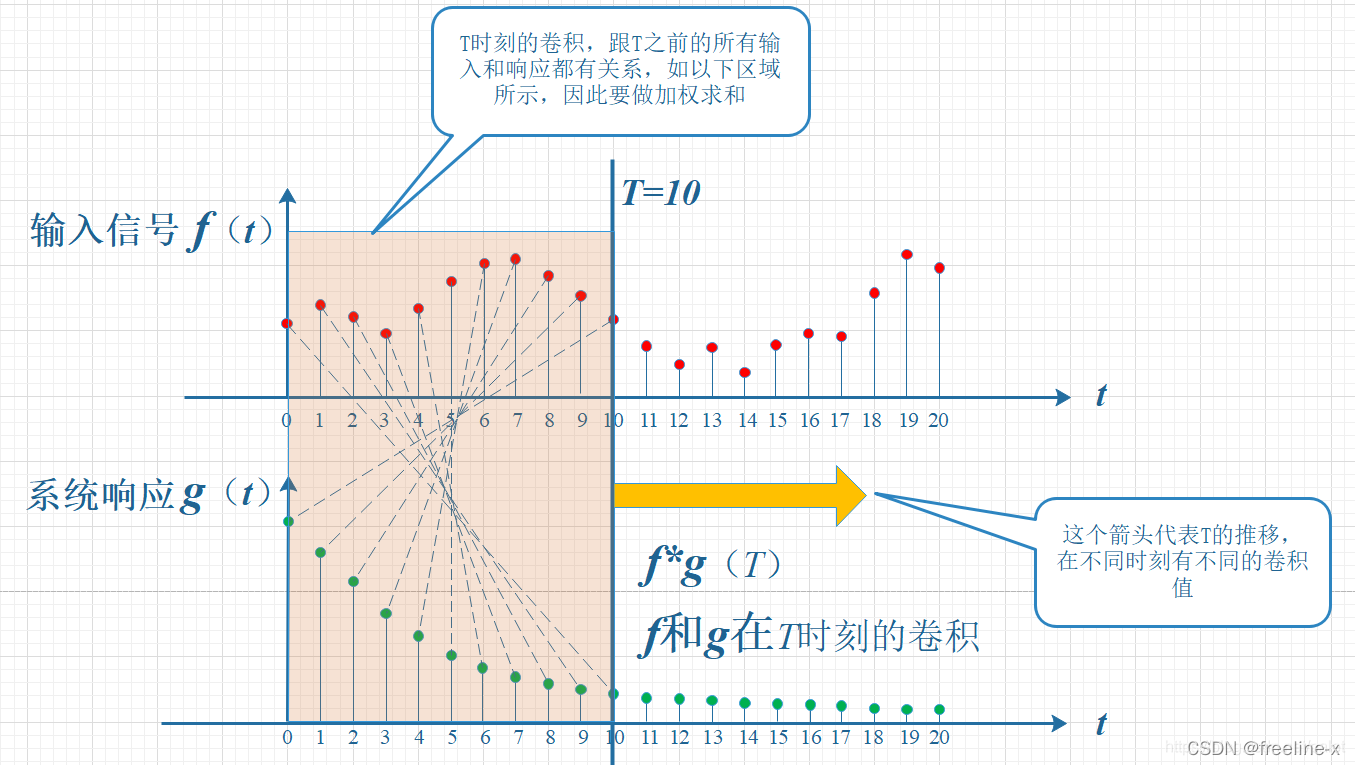
显然,上面的对应关系看上去比较难看,是拧着的,所以,我们把g函数对折一下,变成了g(-t),这样就好看一些了。看到了吗?这就是为什么卷积要“卷”,要翻转的原因,这是从它的物理意义中给出的。
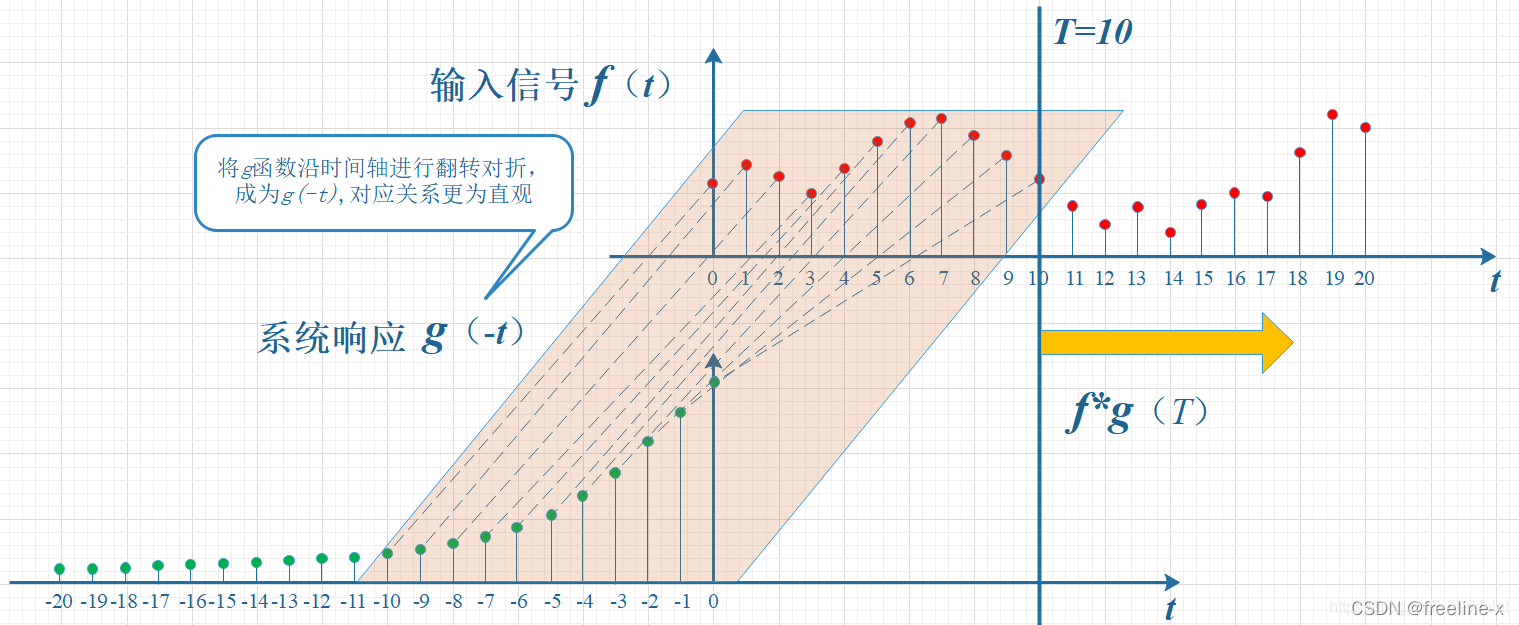 上图虽然没有拧着,已经顺过来了,但看上去还有点错位,所以再进一步平移T个单位,就是下图。它就是本文开始给出的卷积定义的一种图形的表述:
上图虽然没有拧着,已经顺过来了,但看上去还有点错位,所以再进一步平移T个单位,就是下图。它就是本文开始给出的卷积定义的一种图形的表述:
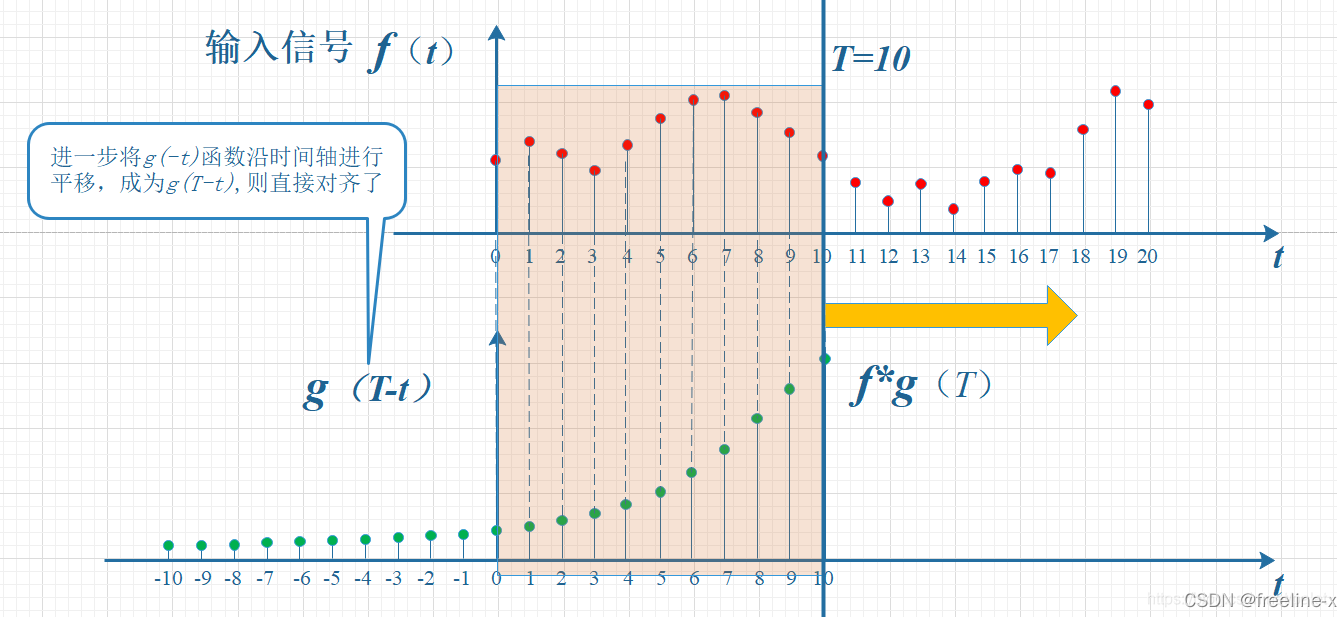 所以,在以上计算T时刻的卷积时,要维持的约束就是: t+ (T-t) = T
所以,在以上计算T时刻的卷积时,要维持的约束就是: t+ (T-t) = T
2、一维离散卷积
2.1 基本概念
h ( i ) = f ( i ) ⊗ g ( i ) = ∑ u = − ∞ ∞ f ( u ) × g ( i − u ) = ∑ u = 0 i f ( u ) × g ( i − u ) h(i) = f(i)\otimes g(i) = \sum_{u=-\infty}^{\infty}f(u)\times g(i-u) = \sum_{u = 0}^{i}f(u)\times g(i-u) h(i)=f(i)⊗g(i)=u=−∞∑∞f(u)×g(i−u)=u=0∑if(u)×g(i−u)
公式中,f(i)为一维离散函数, i ∈ [ 0 , m − 1 ] i\in[0,m-1] i∈[0,m−1],即大小为 1 × m 1\times m 1×m;g(i)为一维离散函数, i ∈ [ 0 , n − 1 ] i\in [0,n-1] i∈[0,n−1];即大小为 1 × n 1\times n 1×n;h(i)为卷积结果, i ∈ [ 0 , m + n − 1 ] i\in [0,m+n-1] i∈[0,m+n−1],即大小为m+n-1。后续应用根据不同情况,可以截取结果为相应大小。
一维原始矩阵与一维模板矩阵向卷积,卷积过程步骤为:
(1)基于卷积定义,将模板矩阵旋转180度
(2)将模板矩阵从左到右在原始矩阵中滑动,计算模板矩阵与原始矩阵交集元素的乘积,该和即为卷积结果对应位置的数值。
原矩阵为:[1 2 3]
模板矩阵为:[4 5]
步骤:
1、模板矩阵旋转180度[5 4]
2、
1 2 3 5 4 4 \begin{array}{clcr} \\ &1&2& 3 \\ 5&4& \\ &4 \end{array} 514423
1 2 3 5 4 4 13 \begin{array}{clcr} \\ & 1 & 2 & 3 \\ & 5 & 4 & \\ 4&13 \end{array} 41513243
1 2 3 5 4 4 13 22 \begin{array}{clcr} \\ & 1 & 2 & 3 \\ & & 5 & 4 & \\ 4&13&22 \end{array} 4113252234
1 2 3 5 4 4 13 22 15 \begin{array}{clcr} \\ & 1 & 2 & 3 \\ & & & 5 & 4 & \\ 4&13&22&15 \end{array} 411322235154
故卷积结果为[4 13 22 15]
2.2 示例图解
在知乎问题 如何通俗易懂地解释卷积中排名第一的 马同学在中举的一个很好的例子
丢骰子
要解决的问题是:有两枚骰子,把它们都抛出去,两枚骰子点数加起来为4的概率是多少?

分析一下,两枚骰子点数加起来为4的情况有三种情况:1+3=4, 2+2=4, 3+1=4即
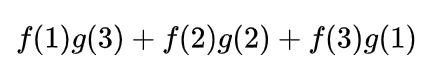
写成卷积的方式就是 ∑ m = 1 3 f ( m ) g ( 4 − m ) \sum_{m=1}^{3}f(m)g(4 - m) ∑m=13f(m)g(4−m)
首先,因为两个骰子的点数和是4,为了满足这个约束条件,我们还是把函数 g 翻转一下,然后阴影区域上下对应的数相乘,然后累加,相当于求自变量为4的卷积值,如下图所示:
 进一步,如此翻转以后,可以方便地进行推广去求两个骰子点数和为 n 时的概率,为f 和 g的卷积 f*g(n),如下图所示:
进一步,如此翻转以后,可以方便地进行推广去求两个骰子点数和为 n 时的概率,为f 和 g的卷积 f*g(n),如下图所示:
 由上图可以看到,函数 g 的滑动,带来的是点数和的增大。这个例子中对f和g的约束条件就是点数和,它也是卷积函数的自变量。有兴趣还可以算算,如果骰子的每个点数出现的概率是均等的,那么两个骰子的点数和n=7的时候,概率最大。
由上图可以看到,函数 g 的滑动,带来的是点数和的增大。这个例子中对f和g的约束条件就是点数和,它也是卷积函数的自变量。有兴趣还可以算算,如果骰子的每个点数出现的概率是均等的,那么两个骰子的点数和n=7的时候,概率最大。
3、二维卷积
3.1 二重积分






3.2 二维连续卷积
二维连续卷积
h ( x , y ) = f ( x , y ) ⊗ g ( x , y ) = ∫ − ∞ ∞ ∫ − ∞ ∞ f ( u , v ) g ( x − u , y − v ) d u d v h(x,y) = f(x,y)\otimes g(x,y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty}f(u,v)g(x-u,y-v)dudv h(x,y)=f(x,y)⊗g(x,y)=∫−∞∞∫−∞∞f(u,v)g(x−u,y−v)dudv
公式中,f(x,y)和g(x,y)为两个二维连续函数
二维连续卷积可以看成给定x,y,u= z(v),对v进行一次卷积,然后在对v卷积
3.3 二维离散卷积
二维离散卷积公式:
h ( i , j ) = ( f ∗ g ) ( i , j ) = f ( i , j ) ⊗ g ( i , j ) = ∑ u = − ∞ ∞ ∑ v = − ∞ ∞ f ( u , v ) g ( i − u , j − v ) = ∑ u = 0 ∞ ∑ v = 0 ∞ f ( u , v ) g ( i − u , j − v ) h(i,j) = (f*g)(i,j) = f(i,j)\otimes g(i,j) = \sum_{u=-\infty}^{\infty}\sum_{v=-\infty}^{\infty}f(u,v)g(i-u,j-v)\\ = \sum_{u=0}^{\infty}\sum_{v=0}^{\infty}f(u,v)g(i-u,j-v) h(i,j)=(f∗g)(i,j)=f(i,j)⊗g(i,j)=u=−∞∑∞v=−∞∑∞f(u,v)g(i−u,j−v)=u=0∑∞v=0∑∞f(u,v)g(i−u,j−v)
公式中,f(i,j)为二维离散函数, i ∈ [ 0 , m − 1 ] , j ∈ [ 0 , n − 1 ] i\in[0,m-1],j\in [0,n-1] i∈[0,m−1],j∈[0,n−1],即大小为 m × n m \times n m×n;g(i,j)为二维离散函数, i ∈ [ 0 , p − 1 ] , j ∈ [ 0 , q − 1 ] i\in[0,p-1],j\in [0,q-1] i∈[0,p−1],j∈[0,q−1],即大小为 p × q p \times q p×q;h(i,j)为卷积结果, i ∈ [ 0 , m + p − 1 ] , j ∈ [ 0 , n + q − 1 ] i\in[0,m+p-1],j\in [0,n+q-1] i∈[0,m+p−1],j∈[0,n+q−1],即大小为 ( m + p − 1 ) × ( n + q − 1 ) (m+p-1)\times (n+q-1) (m+p−1)×(n+q−1)
离散卷积理解为在u和v两个方向去累加
3.4 图像卷积示例
对图像矩阵的理解,图像可以认为是二维函数的离散形式,灰度值相当于z坐标,分辨率大小为x,y
矩阵可以看成是一堆坐标值,在空间
参考:
1、https://www.zhihu.com/question/22298352/answer/637156871 (如何通俗易懂地解释卷积?)
2、数字图像处理 原理与实现