今天来看看二叉树的递归遍历,我们要实现二叉树的先序,中序,后续遍历
这里我们采用的是先序输入
下面是完整代码
#include <stdio.h>
#include <stdlib.h>
struct node
{char data;node *Lchild;node *Rchild;
}tree;
node *creattree(node *l)
{char ch;scanf("%c",&ch);//输入#代表终止 if(ch=='#'){l=NULL;}else{l=(node *)malloc(sizeof(node));l->data=ch;l->Lchild=creattree(l->Lchild);l->Rchild=creattree(l->Rchild);}return l;
}
void preorder(node *l)
{if(l!=NULL){printf("%c",l->data);preorder(l->Lchild);preorder(l->Rchild);}
}
void inorder(node *l)
{if(l!=NULL){inorder(l->Lchild);printf("%c",l->data);inorder(l->Rchild);}
}
void postorder(node *l)
{if(l!=NULL){postorder(l->Lchild);postorder(l->Rchild);printf("%c",l->data);}
}
int main()
{node *l;l=&tree;printf("请输入:");l=creattree(l);printf("先序遍历:");preorder(l);printf("\n中序遍历:");inorder(l);printf("\n后序遍历:");postorder(l);
}
讲一下函数的思路方便理解(当然也有可能讲的不太好。。。)
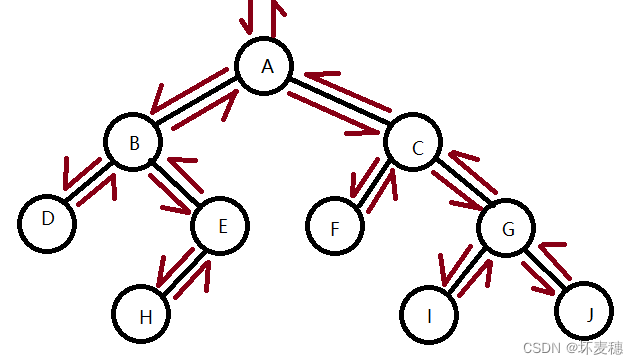
首先我们的输入数据为abc##de#g##f###
二叉树图像为
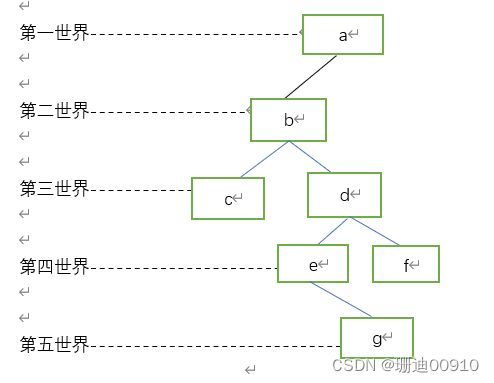
就拿先序来说吧,进入preorder函数后根据先序遍历的定义(简单记为:根左右,先访问根结点,然后是左孩子,左孩子所有的结点访问完了之后在访问右孩子)先打印出根结点的数据a,接着再次调用此函数,进入左孩子l->Lchild,此时我们进入了第二世界,打印出左孩子的数据b,接着再次调用此函数访问l->Lchild的左孩子l->Lchild->Lchild,此时我们进入了第三世界,打印出数据c,再次调用此函数访问l->Lchild->Lchild的左孩子发现为空那么不会进入if语句,那么会出此时的函数回到第二世界,跳到下一个语句调用preorder(l->Rchild)访问l->Lchild->Rchild,进入第三世界,发现也为空,出此时的函数回到第二世界,接着再次调用该函数访问l->Lchild的右孩子l->Lchild->Rchild,此时我们进入了第三世界,打印出数据d,然后再次调用该函数访问l->Lchild->Rchild的左孩子l->Lchild->Rchild->Lchild,此时我们进入了第四世界,打印出数据e,然后再次调用该函数访问l->Lchild->Rchild->Lchild的左孩子,进入第五世界,发现为空,然后我们出这个函数回到第四世界,再次调用这个函数访问l->Lchild->Rchild->Lchild的右孩子,进入第五世界,打印出数据g,同样的访问该结点的左右孩子都为空,回到第四世界,然后结束对l->Lchild->Rchild->Lchild的访问,再次调用函数访问l->Lchild->Rchild->Rchild也就是l->Lchild->Rchild的右孩子,然后调用函数访问l->Lchild->Rchild->Rchild的左右孩子,发现都为空,然后再调用函数访问根结点的右孩子发现为空此时也就结束了二叉树的先序遍历
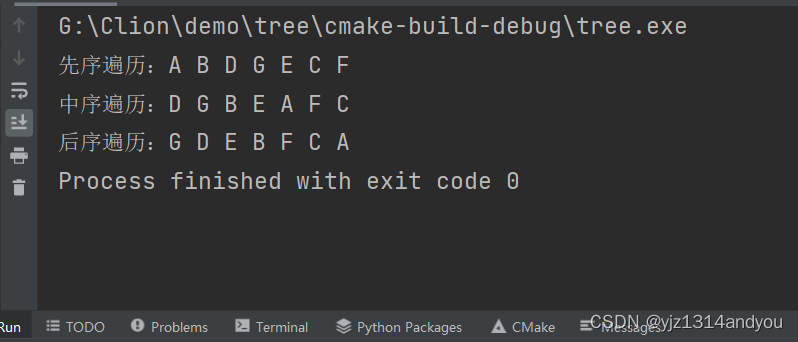
遍历结果为abcdegf
我们来运行测试一下
输入数据后运行结果图为
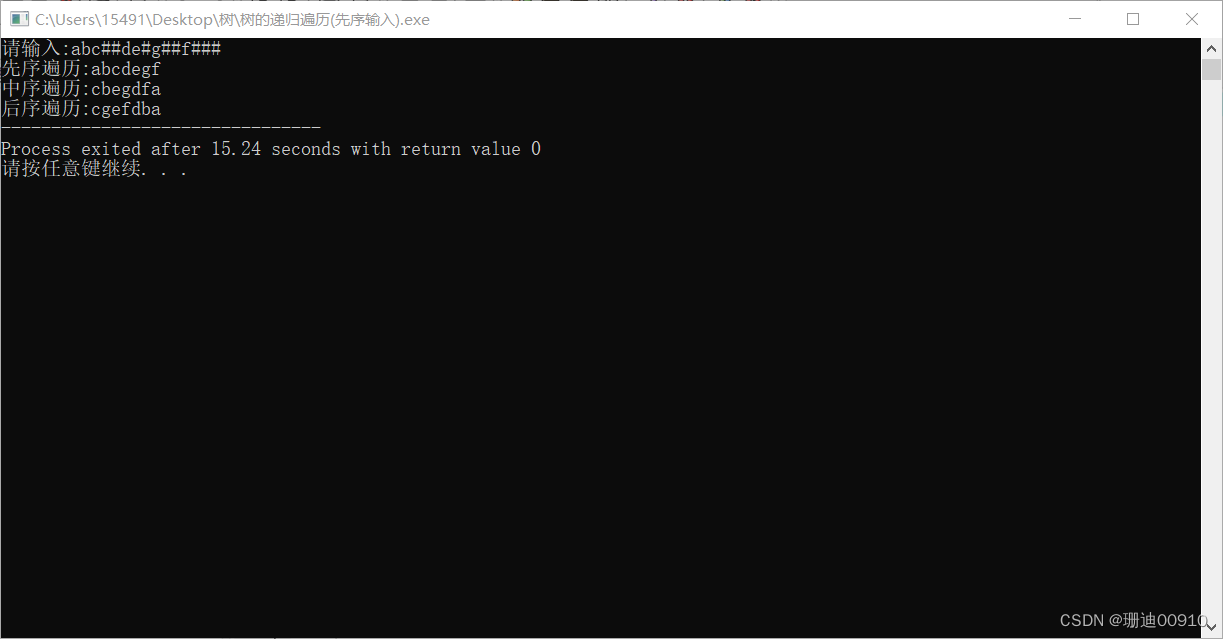
整体上来看非常的绕人,讲的不是很好,如果有错误的地方,望指出