前方有一个人在等着你，你只管勇敢的向前走

采用递归分治的思想，将一个大问题划分成子问题，

对于本题，根据二叉树先序遍历和中序遍历构建二叉树，思路：

我们可以求得根节点左子树的先序和中序序列，以及右子树的先序和中序序列
此问题变成了根据左子树的先序和序列构建左子树的二叉树，根据右子树的先序和中序序列构建右子树的二叉树问题得以分解成子问题

在这里插入图片描述

令先序序列和中序序列在数组中连续存放。

设先序序列第一个字母的数组中的位置为Xb,最后一个字母的数组中的位置为Xe,中序序列第一个字母的位置为Zb,最后一个字母的位置为Ze

从中序序列中，能找到一个节点将当前二叉树分为左子树与右子树，设此节点位于中序序列的k位置

左子树节点个数num=k-Zb

所以左子树的先序序列区间[Xb+1,Xb+num]；中序区间[Zb,k-1]

右子树的先序区间[Xb+num+1,Xe],中序区间[k+1,Ze]

在这里插入图片描述

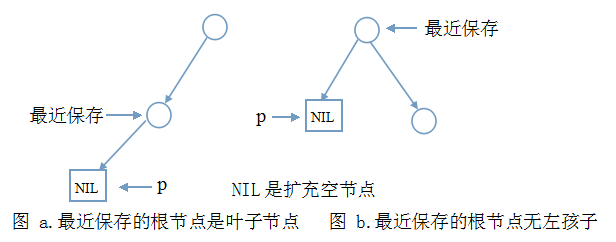
而递归结束的条件是什么呢？

我们可以考虑一下临界条件，即递归的最底层，当先序序列只剩一个节点D时，需要构造该节点，可当先序序列没有了的时候，说明二叉树就到尽头了，所以当先序序列的长度小于等于0时，为递归边界。

代码思路：

定义一个node类型的结构体；

struct node
{char data;node * lchild;node * rchild;
};

步骤一：构造一个创造节点的createNode函数，函数里的参数即为先序序列区间，中序序列区间,createNode（Xb,Xe,Zb,Ze）; 返回值类型为指向 node型的指针。

1.判断是否到达递归边界，到达边界了就返回一个 NULL,即二叉树到达叶子的子节点（叶子节点是不存在子节点的，我就是想表示该节点不存在，不需要构造，要返回上一层，返回到叶子节点）

即判断先序区间长度是否小于等于0，即Xb是否小于等于Xe

2.没到达边界就构造节点


node *Node=new node;node->data=data;

3.在中序序列中找到将中序序列分为左子树和右子树的节点位置k

for (int i = Zb; i <Ze+1; i++){if (xianxu[Xb] == zhongxu[i]){k = i;break;}}

4.递归


Node->lchild=create(Xb，Xe，Zb，Ze)；Node->rchild=create(Xb，Xe，Zb，Ze)

代码

//根据先序中序，构造后序
#include <iostream>
#include <string>
using namespace std;
struct node
{char data;node * lchild;node * rchild;
};
node *createNode(int Xb, int Xe, int Zb, int Ze,string xianxu,string zhongxu);
void houxu(node *Node);int main()
{string xianxu;string zhongxu;while (cin >> xianxu) {cin >> zhongxu;int Xb, Xe, Zb, Ze;//Xb表示先序开始字符位置Xe表示先序结束字符位置 Zb表示中序开始字符位置,Ze表示中序结束字符位置Xb = Zb = 0;Xe = xianxu.length() - 1;Ze = zhongxu.length() - 1;node *Node = new node;Node = createNode(Xb, Xe, Zb, Ze, xianxu, zhongxu);houxu(Node);}system("pause");return 0;
}
node *createNode(int Xb, int Xe, int Zb, int Ze,string xianxu,string zhongxu)
{if(Xb >Xe)return NULL;node *Node = new node;Node->data = xianxu[Xb];int k=0;for (int i = Zb; i <Ze+1; i++){if (xianxu[Xb] == zhongxu[i]){k = i;break;}}Node->lchild = createNode(Xb + 1, Xb+k-Zb, Zb, k - 1, xianxu, zhongxu);Node->rchild = createNode(Xb+k-Zb + 1, Xe, k + 1, Ze, xianxu, zhongxu);return Node;}
void houxu(node *Node)
{if (Node == NULL)return;houxu(Node->lchild);houxu(Node->rchild);cout << Node->data;
}