二叉树前序、中序、后序遍历非递归写法的透彻解析

前言

在前两篇文章二叉树和二叉搜索树中已经涉及到了二叉树的三种遍历。递归写法，只要理解思想，几行代码。可是非递归写法却很不容易。这里特地总结下，透彻解析它们的非递归写法。其中，中序遍历的非递归写法最简单，后序遍历最难。我们的讨论基础是这样的：

//Binary Tree Node
typedef struct node
{int data;struct node* lchild;  //左孩子struct node* rchild;  //右孩子
}BTNode;

首先，有一点是明确的：非递归写法一定会用到栈，这个应该不用太多的解释。我们先看中序遍历：

中序遍历

分析

中序遍历的递归定义：先左子树，后根节点，再右子树。如何写非递归代码呢？一句话：让代码跟着思维走。我们的思维是什么？思维就是中序遍历的路径。假设，你面前有一棵二叉树，现要求你写出它的中序遍历序列。如果你对中序遍历理解透彻的话，你肯定先找到左子树的最下边的节点。那么下面的代码就是理所当然的：

中序代码段(i)

BTNode* p = root;  //p指向树根
stack<BTNode*> s;  //STL中的栈
//一直遍历到左子树最下边，边遍历边保存根节点到栈中
while (p)
{s.push(p);p = p->lchild;
}

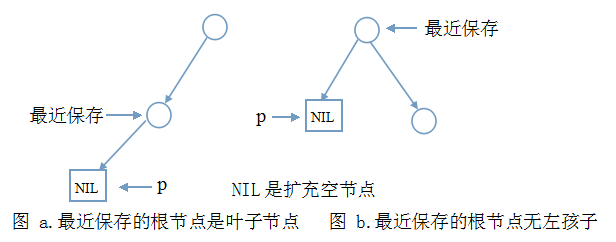
保存一路走过的根节点的理由是：中序遍历的需要，遍历完左子树后，需要借助根节点进入右子树。代码走到这里，指针p为空，此时无非两种情况：

说明：

上图中只给出了必要的节点和边，其它的边和节点与讨论无关，不必画出。
你可能认为图a中最近保存节点算不得是根节点。如果你看过树、二叉树基础，使用扩充二叉树的概念，就可以解释。总之，不用纠结这个没有意义问题。
整个二叉树只有一个根节点的情况可以划到图a。

仔细想想，二叉树的左子树，最下边是不是上图两种情况？不管怎样，此时都要出栈，并访问该节点。这个节点就是中序序列的第一个节点。根据我们的思维，代码应该是这样：

p = s.top();
s.pop();
cout << p->data;

我们的思维接着走，两图情形不同得区别对待：

1.图a中访问的是一个左孩子，按中序遍历顺序，接下来应访问它的根节点。也就是图a中的另一个节点，高兴的是它已被保存在栈中。我们只需这样的代码和上一步一样的代码：

p = s.top();
s.pop();
cout << p->data;

左孩子和根都访问完了，接着就是右孩子了，对吧。接下来只需一句代码：p=p->rchild;在右子树中，又会新一轮的代码段(i)、代码段(ii)……直到栈空且p空。

2.再看图b，由于没有左孩子，根节点就是中序序列中第一个，然后直接是进入右子树：p=p->rchild;在右子树中，又会新一轮的代码段(i)、代码段(ii)……直到栈空且p空。

思维到这里，似乎很不清晰，真的要区分吗？根据图a接下来的代码段(ii)这样的：

p = s.top();
s.pop();
cout << p->data;
p = s.top();
s.pop();
cout << p->data;
p = p->rchild;

根据图b，代码段(ii)又是这样的：

p = s.top();
s.pop();
cout << p->data;
p = p->rchild;

我们可小结下：遍历过程是个循环，并且按代码段(i)、代码段(ii)构成一次循环体，循环直到栈空且p空为止。

不同的处理方法很让人抓狂，可统一处理吗？真的是可以的！回顾扩充二叉树，是不是每个节点都可以看成是根节点呢？那么，代码只需统一写成图b的这种形式。也就是说代码段(ii)统一是这样的：

中序代码段(ii)

p = s.top();
s.pop();
cout << p->data;
p = p->rchild;

口说无凭，得经的过理论检验。

图a的代码段(ii)也可写成图b的理由是：由于是叶子节点，p=-=p->rchild;之后p肯定为空。为空，还需经过新一轮的代码段(i)吗？显然不需。(因为不满足循环条件)那就直接进入代码段(ii)。看！最后还是一样的吧。还是连续出栈两次。看到这里，要仔细想想哦！相信你一定会明白的。

这时写出遍历循环体就不难了：

BTNode* p = root;
stack<BTNode*> s;
while (!s.empty() || p)
{//代码段(i)一直遍历到左子树最下边，边遍历边保存根节点到栈中while (p){s.push(p);p = p->lchild;}//代码段(ii)当p为空时，说明已经到达左子树最下边，这时需要出栈了if (!s.empty()){p = s.top();s.pop();cout << setw(4) << p->data;//进入右子树，开始新的一轮左子树遍历(这是递归的自我实现)p = p->rchild;}
}

仔细想想，上述代码是不是根据我们的思维走向而写出来的呢？再加上边界条件的检测，中序遍历非递归形式的完整代码是这样的：

中序遍历代码一

//中序遍历
void InOrderWithoutRecursion1(BTNode* root)
{//空树if (root == NULL)return;//树非空BTNode* p = root;stack<BTNode*> s;while (!s.empty() || p){//一直遍历到左子树最下边，边遍历边保存根节点到栈中while (p){s.push(p);p = p->lchild;}//当p为空时，说明已经到达左子树最下边，这时需要出栈了if (!s.empty()){p = s.top();s.pop();cout << setw(4) << p->data;//进入右子树，开始新的一轮左子树遍历(这是递归的自我实现)p = p->rchild;}}
}

恭喜你，你已经完成了中序遍历非递归形式的代码了。回顾一下难吗？

接下来的这份代码，本质上是一样的，相信不用我解释，你也能看懂的。

中序遍历代码二

//中序遍历
void InOrderWithoutRecursion2(BTNode* root)
{//空树if (root == NULL)return;//树非空BTNode* p = root;stack<BTNode*> s;while (!s.empty() || p){if (p){s.push(p);p = p->lchild;}else{p = s.top();s.pop();cout << setw(4) << p->data;p = p->rchild;}}
}

前序遍历

分析

前序遍历的递归定义：先根节点，后左子树，再右子树。有了中序遍历的基础，不用我再像中序遍历那样引导了吧。

首先，我们遍历左子树，边遍历边打印，并把根节点存入栈中，以后需借助这些节点进入右子树开启新一轮的循环。还得重复一句：所有的节点都可看做是根节点。根据思维走向，写出代码段(i):

前序代码段(i)

//边遍历边打印，并存入栈中，以后需要借助这些根节点(不要怀疑这种说法哦)进入右子树
while (p)
{cout << setw(4) << p->data;s.push(p);p = p->lchild;
}

接下来就是：出栈，根据栈顶节点进入右子树。

前序代码段(ii)

//当p为空时，说明根和左子树都遍历完了，该进入右子树了
if (!s.empty())
{p = s.top();s.pop();p = p->rchild;
}

同样地，代码段(i)(ii)构成了一次完整的循环体。至此，不难写出完整的前序遍历的非递归写法。

前序遍历代码一

void PreOrderWithoutRecursion1(BTNode* root)
{if (root == NULL)return;BTNode* p = root;stack<BTNode*> s;while (!s.empty() || p){//边遍历边打印，并存入栈中，以后需要借助这些根节点(不要怀疑这种说法哦)进入右子树while (p){cout << setw(4) << p->data;s.push(p);p = p->lchild;}//当p为空时，说明根和左子树都遍历完了，该进入右子树了if (!s.empty()){p = s.top();s.pop();p = p->rchild;}}cout << endl;
}

下面给出，本质是一样的另一段代码：

前序遍历代码二

//前序遍历
void PreOrderWithoutRecursion2(BTNode* root)
{if (root == NULL)return;BTNode* p = root;stack<BTNode*> s;while (!s.empty() || p){if (p){cout << setw(4) << p->data;s.push(p);p = p->lchild;}else{p = s.top();s.pop();p = p->rchild;}}cout << endl;
}

在二叉树中使用的是这样的写法，略有差别，本质上也是一样的：

前序遍历代码三

void PreOrderWithoutRecursion3(BTNode* root)
{if (root == NULL)return;stack<BTNode*> s;BTNode* p = root;s.push(root);while (!s.empty())  //循环结束条件与前两种不一样{//这句表明p在循环中总是非空的cout << setw(4) << p->data;/*栈的特点：先进后出先被访问的根节点的右子树后被访问*/if (p->rchild)s.push(p->rchild);if (p->lchild)p = p->lchild;else{//左子树访问完了，访问右子树p = s.top();s.pop();}}cout << endl;
}

最后进入最难的后序遍历：

后序遍历

分析

后序遍历递归定义：先左子树，后右子树，再根节点。后序遍历的难点在于：需要判断上次访问的节点是位于左子树，还是右子树。若是位于左子树，则需跳过根节点，先进入右子树，再回头访问根节点；若是位于右子树，则直接访问根节点。直接看代码，代码中有详细的注释。

后序遍历代码一

//后序遍历
void PostOrderWithoutRecursion(BTNode* root)
{if (root == NULL)return;stack<BTNode*> s;//pCur:当前访问节点，pLastVisit:上次访问节点BTNode* pCur, *pLastVisit;//pCur = root;pCur = root;pLastVisit = NULL;//先把pCur移动到左子树最下边while (pCur){s.push(pCur);pCur = pCur->lchild;}while (!s.empty()){//走到这里，pCur都是空，并已经遍历到左子树底端(看成扩充二叉树，则空，亦是某棵树的左孩子)pCur = s.top();s.pop();//一个根节点被访问的前提是：无右子树或右子树已被访问过if (pCur->rchild == NULL || pCur->rchild == pLastVisit){cout << setw(4) << pCur->data;//修改最近被访问的节点pLastVisit = pCur;}/*这里的else语句可换成带条件的else if:else if (pCur->lchild == pLastVisit)//若左子树刚被访问过，则需先进入右子树(根节点需再次入栈)因为：上面的条件没通过就一定是下面的条件满足。仔细想想！*/else{//根节点再次入栈s.push(pCur);//进入右子树，且可肯定右子树一定不为空pCur = pCur->rchild;while (pCur){s.push(pCur);pCur = pCur->lchild;}}}cout << endl;
}

下面给出另一种思路下的代码。它的想法是：给每个节点附加一个标记(left,right)。如果该节点的左子树已被访问过则置标记为left；若右子树被访问过，则置标记为right。显然，只有当节点的标记位是right时，才可访问该节点；否则，必须先进入它的右子树。详细细节看代码中的注释。

后序遍历代码二

//定义枚举类型：Tag
enum Tag{left,right};
//自定义新的类型，把二叉树节点和标记封装在一起
typedef struct
{BTNode* node;Tag tag;
}TagNode;    
//后序遍历  
void PostOrderWithoutRecursion2(BTNode* root)
{if (root == NULL)return;stack<TagNode> s;TagNode tagnode;BTNode* p = root;while (!s.empty() || p){while (p){tagnode.node = p;//该节点的左子树被访问过tagnode.tag = Tag::left;s.push(tagnode);p = p->lchild;}tagnode = s.top();s.pop();//左子树被访问过，则还需进入右子树if (tagnode.tag == Tag::left){//置换标记tagnode.tag = Tag::right;//再次入栈s.push(tagnode);p = tagnode.node;//进入右子树p = p->rchild;}else//右子树已被访问过，则可访问当前节点{cout << setw(4) << (tagnode.node)->data;//置空，再次出栈(这一步是理解的难点)p = NULL;}}cout << endl;
}<span style="font-family: 'Courier New'; ">  </span>