二叉树的遍历分为  先序遍历，中序遍历，后序遍历，层次遍历  四种遍历。

　　这节要分享的是先序遍历

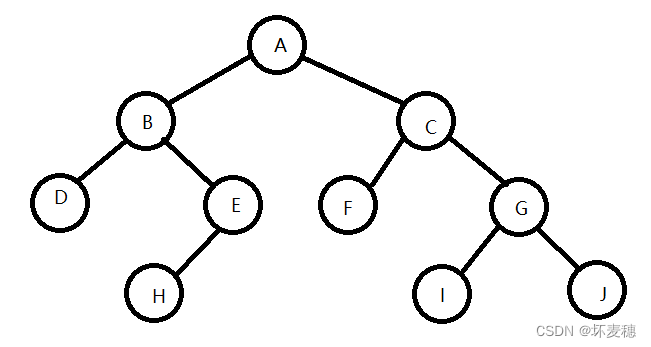
　　如图所示，这是一个普通的二叉树。他的先序遍历是：A B D E H C F G  I J 

　　为什么呢？

　　先序遍历的遍历规则是：根 左 右　！！！

        详解：先遍历根结点Ａ，

　　遍历左子树的根结点Ｂ，

　　遍历Ｂ的左子树根结点Ｄ，

　　Ｄ为叶子节点，遍历Ｂ的右子树根节点Ｅ，

　　遍历Ｅ的左子树根节点Ｈ，

　　Ｈ为叶子节点且Ａ的左子树已遍历完，遍历Ａ的右子树根节点Ｃ，

　　遍历C的左子树根节点F，

　　Ｆ为叶子节点，遍历Ｃ的右子树根节点Ｇ，

　　遍历Ｇ的左子树根结点 I，

　　I 为叶子节点，遍历Ｇ的右子树根节点Ｊ．

　　最终得：A B D E H C F G  I J 

　　总结：从根结点出发，先遍历根结点，再依次将其左右子树以此规则遍历。

        

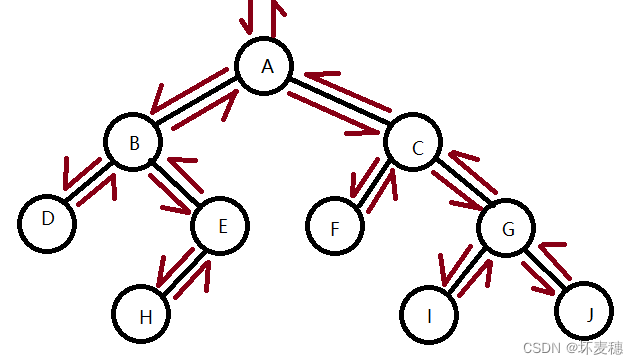
        小技巧：在先序遍历时，进行如图所示的寻找路径，该路径上每个结点被找到第一次时，将它遍历。（即，从Ａ出发，先遍历Ａ，到Ｂ，遍历Ｂ，到Ｄ，遍历Ｄ......）

　　最终，即可得该树的先序遍历为 A B D E H C F G I J 

实现代码：

​
​//利用递归来遍历树
//先序遍历函数
void PreOrder(BitTree &T)
{while (T != NULL){//遍历代码visit(T);//左子树PreOrder(T->lchild);//右子树PreOrder(T->rchild);}
}​